Cabri-FAQ (47)

Antwoord | Constructie | Download  ][  Alle vragen | Meetkunde | Cabri

vorige Vorige    begin Begin     Volgende Volgende 

Vraag 47
Hoe maak je een macro om een gerichte hoek te markeren met een boog en een pijltje?

Antwoord terug

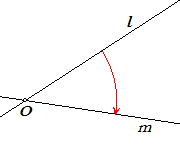faq47_1    Onder de gerichte (ook wel georiënteerde hoek) van twee lijnen l en m, aangegeven met Đ)(l, m), verstaan we
- de draaiingshoek modulo p die l afbeeldt op m, als l en m elkaar snijden;
- 0 als l en m evenwijdig zijn.
Zie ook de pagina CabriFAQ-42.

De te ontwikkelen macro moet een boog opleveren met aan het 'einde' daarvan een pijltje.

We gebruiken bij de te ontwikkelen macro een methode die gebaseerd is op hetgeen is opgemerkt op de pagina CabriFAQ-42, over het meten van geöriënteerde hoeken (ook wel gerichte hoeken genoemd).

Constructiestappen macro:MarkeerGerichteHoek terug

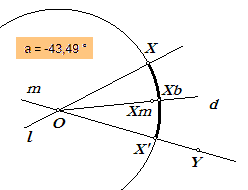faq47_2    1.  Laad de macro:GeorienteerdeHoek (zie pagina CabriFAQ-42, en meet de gerichte hoek tussen de lijnen l en m (snijpunt O) door een punt X op l en een punt Y op m te kiezen.
Dit geeft de waarde a (zie figuur hiernaast).
2.  X' = Rotatie(X, O, a); het punt X' ligt daarmee op de lijn m.
3.  Xm = Midden(X, X')
4.  d = HalveLijn(O, Xm)
5.  Cirkel(O, X)
6.  Xb = Snijpunt(d, '5')
7.  Boog(X, Xb, X')
We hebben nu de boog van de gerichte hoek.
.
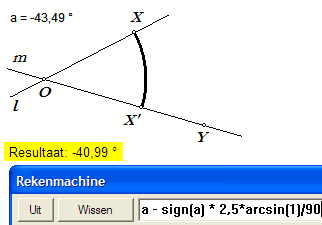faq47-3    Voor het pijltje gebruiken we de ingebouwde Cabri-functie 'Vector'. Hiertoe plaatsen we op 'boog 7' een punt Xv (het beginpunt van de vector) dichtbij X' (booglengte XvX' = 2,5°). Het eindpunt van de vector is dan X'.
Bij een positieve hoek moeten we dan de waarde van a (de gerichte hoek; zie punt 1) verminderen met 2,5°, bij een negatieve hoek juist vermeerderen met 2,5°.
Als de gerichte hoek tussen -2,5° en +2,5° ligt, tekenen we alleen het boogje. Dit laatste houdt in, dat het punt Xv een zogenoemd voorwaardelijk punt is.
Die nieuwe hoek geven we aan met b.

8.  Bereken de waarde van b met de Rekenmachine; zie de figuur hiernaast. Merk op, dat arcsin(1)/90 gelijk is aan 1°. De functie sign berekent het teken, te weten -1, 0, of 1, van het argument.
.
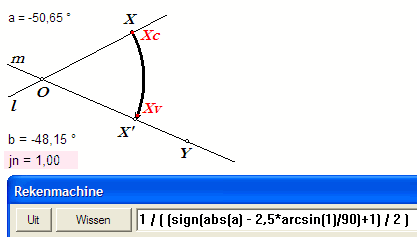faq47_4    9. We moeten nu uitmaken of we het punt Xv moeten tekenen of niet.
We doen dat via de Boole-se 'variabele' jn.
Deze berekenen we met de hiernaast in de Rekenmachine staande uitdrukking.
De waarde van jn is dan:
  1 - als het punt Xv getekend kan worden;
  'bestaat niet' -  als het punt niet getekend hoeft te worden.

Nb. Tijdens de constructie (en de definitie) van de macro moet de waarde van jn gelijk zijn aan 1!

10.  Xc = Vermenigvuldiging(X, O, 'jn'); hiermee wordt het 'voorwaardelijke' punt Xc geplaatst op dezelfde positie als het punt X.
.
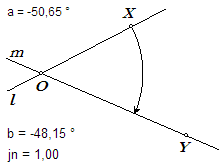faq47_5    Vervolgens (zie bovenstaande figuur):

11.  Xv = Rotatie(Xc, O, 'b'); het punt Xv wordt wel (jn = 1) of niet (jn = 'bestaat niet') geconstrueerd.
12.  Vector(Xv, X'); en dan hebben we ook de vector.

13.  Verberg daarna de punten X', Xv en Xc (en eventueel de gebruikte teksten).

Macro-definitie
- Beginobjecten: X, O, Y (in deze volgorde)
- Eindobjecten: boog (zie punt 7) en vector (zie punt 12).

Klik hier >CabriJavapplet< voor een illustratie van de macro:MarkeerGerichteHoek met een CabriJavapplet.

download Download terug
De hierboven gedefinieerde macro en de daarbij gebruikte figuur (die dezelfde is als de eerste figuur) kunnen via deze website in één bestand worden gedownload.
Klik hier om het download-proces te starten (ZIP-bestand; ca. 10 Kb).
In het bestand zijn macro's voor Cabri II en Cabri Plus opgenomen.

vorige Vorige    begin Begin     Volgende Volgende 

begin pagina
[p:faq47.htm] laatste wijziging op: 16-04-08