Cabri-FAQ (43)

Vorige

Begin

Volgende

Vraag 43
Hoe maak je een macro voor een Apollonius-cirkel bij twee punten bij gegeven verhouding k : 1?

Antwoord

De definitie van de macro is gebaseerd op Oplossing 2 die vermeld is in de theorie over Apollonius-cirkels.
De verhouding k : 1 wordt daar vastgelegd door twee lijnstukken met die lengtes.
Deze lijnstukken zullen we dus met de macro eerst moeten construeren.

De gegeven punten zijn A en B, waarbij het 'gewicht' k bij A hoort, en het 'gewicht' 1 bij B; maw. XA : XB = k : 1.

Een lijnstuk met lengte 1 (één) - We kunnen de lengte van AB meten. Delen we deze lengte door zichzelf (met Cabro's Rekenmachine) dan krijgen we het getal 1 (zie |AB| / |AB| in de figuur bij onderstaand overzicht).
Een lijnstuk met lengte k - Hebben we eenmaal een lijnstuk met lengte 1, dan kan een lijnstuk met lengte k eenvoudig via de functie Vermenigvuldiging worden verkregen (zie stap 8 in onderstaand overzicht).

Constructiestappen

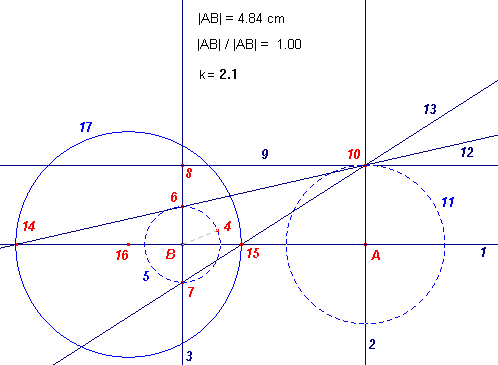1 - Lijn(A, B)
2,3 - Loodlijn(A, 1) en Loodlijn(B, 1)
4 - MaatOverbrengen("getal 1", B)
5 - Cirkel(B, 4)
6,7 - Snijpunten(3, 5)
8 - Vermenigvuldiging(6, B, "getal k")
9 - Loodlijn(8, 3)
10 - Snijpunt(9, 2)
11 - Cirkel(A, 10)
12, 13 - Lijn(10, 6) en Lijn(10, 7)
14, 15 - Snijpunt(12, 1) en Snijpunt(13, 1)
16 - Midden(14, 15)
17 - Cirkel(16, 15)

Nb. Het tekenen van de Cirkel(16, 14) maakt het tekenen van de Apollonius-cirkel voor k = 1 onmogelijk!

Hierna Verbergen: 14, 15, 16

Macro-definitie
Beginobjecten: A, B, "getal k"
Eindobjecten: 17
DefinieerMacro

Download
De hierboven gedefinieerde macro en de daarbij gebruikte figuur kunnen via deze website in één bestand worden gedownload.
Klik hier om het download-proces te starten (ZIP-bestand; ca. 7 Kb).
In het bestand zijn macro's voor Cabri II en Cabri Plus opgenomen.

Vorige

Begin

Volgende

[p:faq43.htm] laatste wijziging op: 10-10-05