Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Meetkundige plaatsen

Wat is een meetkundige plaats?
Opdracht 1
Afhankelijkheid, onafhankelijkheid, pad, animatie
Opdracht 2
Onderzoek
     Opdracht 3
     Opdracht 4
     Opdracht 5
     Opdracht 6
Samenstellende delen van een meetkundige plaats
Opdracht 7
Opdracht 8
Download

Opmerking
Zie ook het Cabri-werkblad "Meetkundige plaatsen, een inleiding" dat een inleiding geeft op he begrip meetkundige plaats.
[einde Opmerking

1. Wat is een meetkundige plaats?
We geven direct maar een

Definitie
Een meetkundige figuur heet meetkundige plaats van punten met een bepaalde eigenschap indien:
1. alle punten van de figuur die bedoelde eigenschap hebben;
2. alle punten met de eigenschap tot de figuur behoren.

Voorbeelden
[1] Een cirkel is de meetkundige plaats van de punten (X) die een gegeven afstand (r) tot een vast punt (M) hebben.
Notatie: {X | XM = r }.
[2] De bissectrice van een hoek is de meetkundige plaats van de punten die gelijke afstand hebben tot de benen van die hoek.
Notatie { X | d(X,a) = d(X, b) }, waarin a en b de benen van de hoek zijn en d de afstandsfunctie is van een punt tot een lijn.
[einde Voorbeelden]

Opdracht 1
Een bekende meetkundige plaats is de middelloodlijn van een lijnstuk (AB). De middelloodlijn is namelijk de meetkundige plaats van de punten die gelijke afstand hebben tot de punten A en B. Notatie { X | XA = XB }.

figuur 1a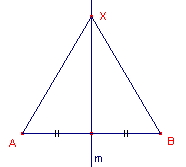

figuur 1b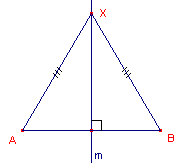

Zoals uit de definitie blijkt moeten we, om de middelloodlijn als meetkundige plaats te mogen aanduiden, TWEE bewijzen geven:
1. alle punten op de middelloodlijn hebben de eigenschap (gelijke afstand);
2. alle punten met de eigenschap (gelijke afstand) liggen op de middelloodlijn.
We moeten dus de uitgangspunten voor het bewijs goed kiezen.
Om het bewijs voor alle punten te leveren volstaat het een bewijs te geven voor een willekeurig punt (X).

a.	We weten: Het punt X ligt op de middelloodlijn van het lijnstuk AB (zie figuur 1a). Bewijs nu: XA = XB.
b.	We weten: Voor het punt X geldt XA = XB (zie figuur 1b). Bewijs nu: X ligt op de middelloodlijn van AB. Aanwijzing Teken de loodlijn uit X op AB en bewijs dat deze lijn door het midden van AB gaat.

_
	Ophalen van de figuur in Cabri Geometry			Animatie met CabriJava	(*)

(*)

Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is geïnstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld.
Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

2. Afhankelijkheid, onafhankelijkheid, pad, animatie

Opdracht 2

figuur 2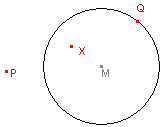

Teken een punt P en een cirkel met middelpunt M (en een willekeurige straal). Zie figuur 2.
Teken het punt Q op de cirkel (met de functie "Punt op object" in het Punt-menu).
Construeer het midden X van het lijnstuk PQ (met de functie "Midden" in het Constructie-menu).
Het is hierbij niet nodig eerst het lijnstuk PQ te tekenen.

a.	Verplaats het punt P. Welke andere objecten veranderen hierdoor ook van positie?
b.	Verplaats het punt Q. Welke andere objecten veranderen nu ook van positie?
c.	Vergroot en/of verklein de cirkel, cq. verplaats het punt M. Welke andere objecten veranderen hierdoor van positie?
d.	Is het mogelijk het punt X direct te verplaatsen?

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Het punt X is afhankelijk van de ligging van de punten P en Q). Het punt Q is op zijn beurt weer afhankelijk van de cirkel met middelpunt M.
We zeggen: X is afhankelijk van P; X is afhankelijk van Q; X is afhankelijk van M; ...
P is een onafhankelijk punt; M is een onafhankelijk punt.
Q kan verplaatst worden op de cirkel. Hierdoor is Q afhankelijk van het object waarop het gedefinieerd is: de cirkel.
De cirkel wordt in dit geval ook wel het pad van het punt Q genoemd.
Deze eigenschap van Q, de ligging ervan op de cirkel (op een pad dus), kan in Cabri gebruikt worden voor de constructie van meetkundige plaatsen.
Nb. Onafhankelijke punten kunnen daarvoor niet worden gebruikt.

Er zijn drie methoden om meetkundige plaatsen op basis van een pad te onderzoeken.
Deze drie methodes komen aan de orde in Opdracht 3 in de paragraaf "3. Onderzoek".

3. Onderzoek
We gaan hierbij uit van de objecten zoals die in paragraaf 2, figuur 2 zijn besproken.

Opdracht 3

a1.

Verplaats het punt Q over de cirkel.
Let daarbij op de positie van het punt X.

Deze methode kan iets worden verfraaid door de verandering van de positie van het punt Q "automatisch" te laten geschieden.
Dit heet Animatie.
In het Extra-menu vinden we de functie "Animatie". Hiermee kan aan een object een "animatieveer" worden gekoppeld, waardoor het object beweegt over het bijbehorende pad.

a2.

Kies de functie "Animatie" in het Extra-menu.
Selecteer het punt Q en houdt de linker muisknop ingedrukt. Sleep nu de muis. Hierdoor bepalen we de grootte van de animatieveer. De lengte van de veer bepaalt de snelheid van de verplaatsing van het punt Q over de cirkel.
Laat hierna de linker muisknop los.
De animatie kan worden gestopt door op het werkblad te klikken.

De methode die is behandeld in Opdracht 2, onderdeel a2, wordt meestal gecombineerd met de optie "Spoor aan/uit" die ook te vinden is in het Extra-menu.
Met "Spoor aan" kan het pad van een (afhankelijk) object worden getekend.

b.	Kies de functie "Spoor aan/uit" in het Extra-menu. Selecteer daarmee het punt X. Verplaats nu het punt Q, met of zonder Animatie, over de cirkel (zie figuur 3).

figuur 3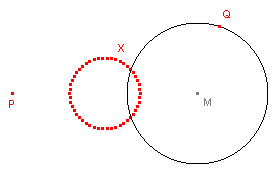

Opmerking
Het spoor van een object kan worden uit gezet door opnieuw de functie "Spoor aan/uit" te kiezen en het object te dé-selecteren (opnieuw aanklikken).
Een getekend spoor kan via het toetsenbord worden gewist met de toetscombinatie [Ctrl + F] of door met de muis te klikken op de rechter schuifknop van het tekenblad.
[einde Opmerking]

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Bij de derde methode van onderzoek van een meetkundige plaats laten we de meetkundige plaats (het pad) van een object door Cabri "berekenen" en tekenen.
Hierbij wordt het pad van het afhankelijke object op het werkblad weergegeven met een vooraf ingesteld aantal punten. Het onafhankelijk punt (het punt Q in dit geval) wordt daarbij niet verplaatst.

c.	Kies de functie "Meetkundige plaats" in het Constructie-menu. Selecteer nu het punt X (het punt waarvan de meetkundige plaats moet worden getekend). Selecteer vervolgens het punt Q (het punt dat als basisobject voor de meetkundige plaats dient).
d.	Geef een zo volledig mogelijke beschrijving van de meetkundige plaats van het midden X van het lijnstuk PQ als Q de cirkel doorloopt. Onder "zo volledig mogelijk" wordt hier verstaan: de ligging van het middelpunt van de meetkundige plaats en de grootte van de straal.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Opmerkingen
[1]
Cabri herkent de meetkundige plaats uit deze opdracht niet als een cirkel (wij wel?).
Op een door Cabri geconstrueerde meetkundige plaats kunnen met de functie "Punt op object" (in het Punt-menu) wel punten worden getekend.
Hiermee kan in voorkomende gevallen de meetkundige plaats door de gebruiker zelf worden geconstrueerd.

[2] BELANGRIJK!
De functie "Meetkundige plaats" in het Constructie-menu van Cabri werkt alleen als het object waarvan de meetkundige plaats moet worden getekend, afhankelijk is van een punt op een pad.
[einde Opmerkingen]

Opdracht 4
Lees allereerst Opmerking [1] aan het einde van Opdracht 3 nog eens.

Kies drie punten op de door Cabri getekende meetkundige plaats (met de functie "Punt op object").
Construeer nu het middelpunt van de meetkundige plaats van het punt X.
Construeer nu ook de cirkel zelf met de functie "Cirkel" in het Cirkel-menu.

Opdracht 5
Iemand anders heeft het middelpunt van de meetkundige plaats volgens het volgende voorschrift geconstrueerd:

Teken de lijn door de punten P en M.
Teken de lijn door de punten Q en M.
Teken de lijn door X evenwijdig met de lijn QM.
Bepaal M_x als snijpunt van de laatste lijn en de lijn PM (zie figuur 4).

figuur 4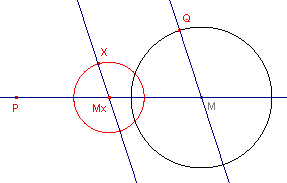

Is deze constructie juist?
Verklaar je antwoord.Ga onder andere na, dat bij verplaatsing van Q op de cirkel de lijn door X ook steeds door M_x gaat.
Teken ook de lijn door P en Q.
Bewijs nu dat de meetkundige plaats van de punten X de cirkel is met middelpunt M_x (het midden van PM) en waarvan de straal gelijk is aan de helft van de straal van cirkel M.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Opdracht 6
Lees allereerst Opmerking [2] aan het einde van Opdracht 3 nog eens.

figuur 5a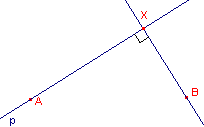

Teken op een nieuw Cabri werkblad de punten A en B.
Teken een lijn p door het punt A.
Construeer de loodlijn uit B op de lijn p.
Het voetpunt van de loodlijn is het punt X op de lijn p (zie figuur 5a).
Zet het Spoor van het punt X aan.
Draai nu de lijn p om het punt A. Dit gaat door de lijn te selecteren (deze lijn) en daarna met ingedrukte linker muisknop de lijn te slepen.

figuur 5b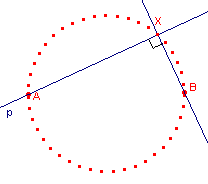

figuur 5c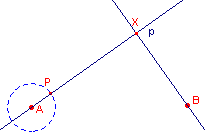

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Opmerking
Je kan ook een animatieveer aan de lijn p koppelen met de functie "Animatie" in het Extra-menu.
[einde Opmerking]

Probeer ook de optie "Meetkundige plaats" uit het Constructie-menu.
Klik op het punt X en daarna op de lijn p.
Waarom werkt deze optie niet?

Kies een nieuw werkblad.
Teken daarop het punt A en een (hulp)cirkel met middelpunt A.
Teken het punt P op deze cirkel.
Teken de lijn p door de punten A en P (zie figuur 5c).
Merk op, dat p nu niet meer direct kan worden gedraaid om het punt A. p is nu afhankelijk van het punt P.
Teken ook het punt B en de loodlijn uit B op p met voetpunt X.
Kies nu de functie "Meetkundige plaats" en klik op X en daarna op P.

Geef nu een volledige beschrijving van de gevonden meetkundige plaats.

4. Samenstellende delen van een meetkundige plaats

Opdracht 7

figuur 6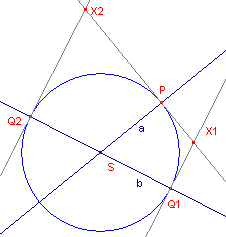

Teken op een nieuw Cabri werkblad twee elkaar in het punt S snijdende lijnen a en b.
Kies het punt P op de lijn a.
Teken de cirkel (S, SP) - middelpunt S, straal = SP.
De snijpunten van deze cirkel met de lijn b zijn de punten Q₁ en Q₂.
Teken ook de raaklijnen in de punten P, Q₁ en Q₂ aan de cirkel.
Deze raaklijnen snijden elkaar in X₁ en X₂ (zie figuur 6).
Construeer de meetkundige plaats van de punten X₁ en X₂ als P de lijn a doorloopt.

Geef een volledige beschrijving van de gevonden meetkundige plaats.
Omschrijf de meetkundige plaats ook in woorden. Dus iets als "De meetkundige plaats van de punten die ....., wordt gevormd door .....".

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Je hebt in Opdracht 7 gezien dat de meetkundige plaats uit twee (vier?) delen is opgebouwd.
Ook bij andere meetkundige plaatsen vind je soms een dergelijke opbouw.

Opdracht 8

Teken op een nieuw werkblad een halve lijn a met eindpunt S.
Kies het punt P op die halve lijn. Teken het lijnstuk SP.
Teken vervolgens twee punten A en B.
Kies de functie "Passer" in het Constructie-menu.
Selecteer A en het lijnstuk PS.
Selecteer B en het lijnstuk PS (zie figuur 7).

figuur 7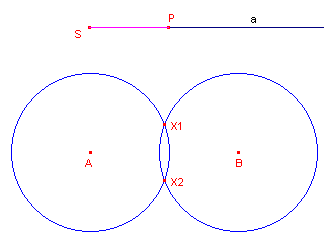

Noem de snijpunten van beide cirkels X₁ en X₂.
Construeer de meetkundige plaats van de punten X₁ en X₂.

Tekent Cabri de volledige meetkundige plaats? Geef een korte toelichting bij je antwoord.
Gebruik ook de functie "Spoor" en verplaats P zelf.
Ontstaat er nu een betere weergave van de meetkundige plaats? Geef een korte toelichting bij je antwoord.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

5. Download
De hierboven gebruikte Cabri figuren zijn in een bestand te downloaden via deze website.
Klik hier om het downloaden van dit bestand te starten [4Kb, ZIP formaat].

Het werkblad zelf is ook beschikbaar in PDF-formaat.
meetkpl.pdf [54Kb]

[meetkpl.htm] laatste wijziging op: 24-08-2001