Cabri werkblad
Overzicht ][ Alle werkbladen | Meetkunde | Cabri
Overzicht - Machtlijn van twee cirkels
Zie ook de pagina "De macht van een punt tov. een cirkel".
Opdracht 1
- Teken een cirkel met middelpunt A en een cirkel met middelpunt B die elkaar snijden in de punten P en Q.
- Teken ook de lijn PQ.
- Kies nu een punt R op deze lijn (via "Punt op object" in het Punt-menu (ook wel Teken1-menu genoemd).
Het punt R heeft een bijzondere eigenschap die we in Opdracht 2 verder zullen onderzoeken.
| [figuur 1] | 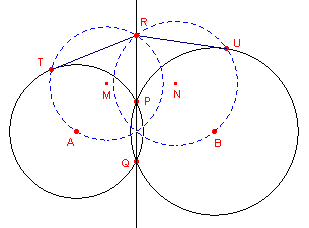 |
Voordat we dat doen, maken we echter eerst een macro die de raaklijnstukken uit R aan beide cirkels tekent (we doen dat omdat we zulke raaklijnstukken verderop ook nodig zullen hebben; zie eventueel ook
Teachers Info nummer 15 van mei 1999).- Construeer het midden M van AR en het midden N van BR met de functie "Midden" in het Constructie-menu (Construeer1-menu).
- Teken de cirkel met middelpunt M die door A gaat en de cirkel met middelpunt N die door B gaat.
- Bepaal vervolgens de snijpunten T en U (zie figuur 1).
- Teken de lijnstukken RT en RU, de raaklijnstukken.
We leggen vervolgens de macro vast.
- Verberg daartoe eerst de punten M en N en de twee cirkels die daarbij horen.
- Kies: "Beginobjecten" in het Macro-menu.
- Wijs aan: het punt R aan, en daarna beide cirkels.
- Kies: "Eindobjecten" in het Macro-menu.
- Wijs aan: het lijnstuk RT en daarna het lijnstuk RU.
- Kies: "Definieer macro" in het Macro-menu. In het aparte menu kunnen we dan de naam van de macro (bijvoorbeeld "Raaklijnstukken") vastleggen. Eventueel kunnen we de macro in een bestand opslaan.
| [figuur 2] | 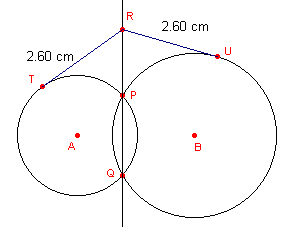 |
| . |
| (*) | Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri
II is geïnstalleerd op het
gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II
Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld. Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren. Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download). |
Je kan ook de cirkel B of de cirkel A vergroten of verkleinen (maar de cirkels moeten
elkaar wel blijven snijden; waarom?).
De lijn PQ heet de machtlijn van de snijdende cirkels. Elk punt van die machtlijn
heeft de eigenschap dat de raaklijnstukken uit een punt aan de beide cirkels gelijke
lengte hebben. We zeggen ook wel:
"De meetkundige plaats van de punten met gelijke raaklijnstukken aan twee cirkels is de machtlijn van die cirkels".
In de laatste zin komt het woordje "snijdende" niet voor. Geldt die
eigenschap dan ook voor niet-snijdende cirkels?
We gaan op onderzoek.
| [figuur 3] | 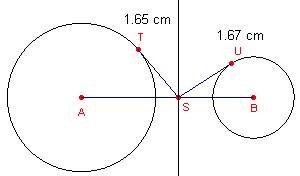 |
We hebben nu een punt (het punt S) gevonden dat op de machtlijn van beide cirkels ligt.
- Verplaats het punt S nu niet meer!
- Teken de loodlijn in S op het lijnstuk AB (met de functie "Loodlijn" in het Construeer-menu").
- Kies op de loodlijn nu het punt R en teken de raaklijnstukken uit R aan beide cirkels.
- Bepaal ook de lengte van die stukken.
- Verplaats het punt R over de loodlijn.
Wat valt je nu (weer) op bij de lengtes van de raaklijnstukken?
De getekende loodlijn is dus de machtlijn van beide cirkels.
In opdracht 4 hebben we de machtlijn "proefondervindelijk" gevonden. We zullen nu een constructie van de machtlijn proberen te vinden (we doen dat in opdracht 6).
Bekijk daartoe eerst de volgende figuur.
| [figuur 4] | 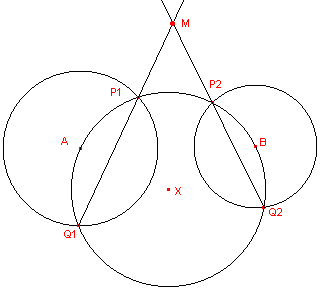 |
Daarin staan weer de cirkels A en B. De derde cirkel met middelpunt X gaat door de punten A en B.
- Ga met behulp van een Cabri-figuur na, dat bij wijziging van de positie van de cirkels A en B, de cirkel X steeds een snijdende cirkel is.
Het punt M (het snijpunt van twee machtlijnen van snijdende cirkels) bestaat dus steeds.
Dus: M ligt op de ..... van de cirkels A en B.
- Ga het bovenstaande na met behulp van een Cabri-figuur (kies daartoe eerst een nieuw werkblad).
Het punt M heet het machtpunt van de drie cirkels.
We gaan er nu van uit dat de cirkels A en B al op een (nieuw) werkblad staan.
- Teken het lijnstuk AB.
- Teken de middelloodlijn van het lijnstuk AB en kies hierop het punt X.
- Teken met behulp van de cirkel X (die gaat door het punt A, en dus ook door het punt B) de machtlijn P1Q1 van de cirkels A en X en de machtlijn P2Q2 van de cirkels B en X.
- Teken het punt M.
- Teken de loodlijn uit M op AB.
Bewijs nu dat deze loodlijn de machtlijn is van de cirkels A en B.
- Ga na, dat de machtlijn steeds door de snijpunten van de cirkels A en B gaat door verplaatsing van (bijvoorbeeld) het punt B.
- Maak een macro die het machtpunt van drie gegeven cirkels tekent.
Download
De op deze pagina staande Cabri-figuren zijn in één bestand
via deze website te downloaden.
Naast deze figuren zijn in het bestand ook enkele niet-behandelde figuren en een drietal
Cabri-macro's opgenomen.
Klik hier om het dowloaden te
starten [ZIP-bestand, ca. 20Kb]
Van deze pagina is ook een PDF-versie
beschikbaar.
![]() machtlijn.pdf [ca. 34Kb]
machtlijn.pdf [ca. 34Kb]
[machtlijn.htm] laatste wijziging op: 25-03-2000