Absolute elementen in het projectieve vlak

Overzicht ][ Proj.Meetkunde | Meetkunde

Overzicht terug

  1. Afspraken en definities cabrisignal
  2. Cirkeleigenschappen cabrisignal
  3. Orthogonale cirkels
  4. Cirkelbundels
  5. Concentrische cirkels
  6. Hoogtepunt en rechte van Euler cabrisignal
         Omcentrum / Zwaartepunt
  7. Negenpuntscirkel cabrisignal
  8. Download

1. Afspraken en definities terug
A. Kies een vaste lijn in het (projectieve) vlak. Noem deze lijn l¥ .
figuur 1a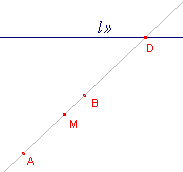

abselem1		 Spreek af:
     Punten op deze lijn heten oneigenlijke punten.
     Punten niet op die lijn heten reële punten.
Spreek af:
     Lijnen waarvan het snijpunt op l¥ ligt, heten parallelle lijnen.
Spreek af:
     Een punt M is het midden van het lijnstuk AB indien (ABMD) = -1
     waarbij D het snijpunt is van de drager van AB en de lijn l¥ .

Opm. In de figuren op deze pagina wordt l¥ meestal  aangegeven met l».
De lijn is ook herkenbaar aan de erop liggende punten I en J.
.
figuur 1b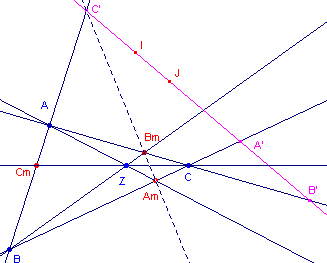

abselemz
Stelling 1
De verbindingslijn van de middens van twee zijden van een driehoek is parallel met de derde zijde van die driehoek.

Bewijs:

 (zie figuur 1b)
Am, Bm, Cm zijn de middens van de zijden van driehoek ABC.
Bekijk de volledige vierhoek ABAmBm. De punten Z, B’ en C’ vormen de diagonaaldriehoek daarvan. AmBm gaat dus door C’. ¨

Gevolg

De zwaartelijnen van een driehoek gaan door één punt, het zwaartepunt Z.
[einde Gevolg]

Klik hier Animatie voor een CabriJavapplet ter illustratie.

B.

Kies op l¥ twee (willekeurige, maar) vaste punten I en J.

figuur 1c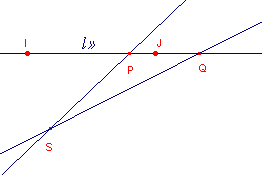

abselem2		 Spreek af:
Lijn a staat loodrecht op lijn b (met a¥ = P en b¥ = Q) DESDA (P Q I J) = -1

Gevolg

Wanneer twee loodrechte lijnen om hun snijpunt draaien, krijgen we een involutie op de lijn l¥ met dubbelpunten I en J.
[einde Gevolg]

De oneigenlijke rechte en de punten I en J heten absolute elementen van het (projectieve) vlak.
Definitie
Een kegelsnede die door I en J gaat, heet cirkel.
.
figuur 2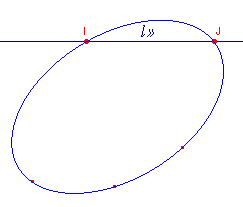

abselem3		 Gevolg
Een kegelsnede is bepaald door 5 punten. Een cirkel is dan dus bepaald door 3 reële punten.
Als deze drie punten collineair zijn, ontaardt de kegelsnede in twee rechte lijnen, de reële lijn en de lijn l¥ .
[einde Gevolg]
.
Definitie
De pool van l¥ ten opzichte van een kegelsnede heet middelpunt van die kegelsnede.
Een koorde door het middelpunt heet middellijn.
.
Stelling 2
Het middelpunt M van een kegelsnede is midden van elke middellijn van die kegelsnede.

Bewijs:
figuur 3 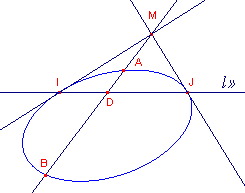abselem4 Zie figuur 3.
Hierin is op basis van de definities uit de pooltheorie:
   (ABMD) = -1 ¨

2. Cirkeleigenschappen terug
Stelling 3 (stelling van Thales)
Voor elk punt P van een cirkel met middellijn AB geldt: PA _|_ PB.

Bewijs:
figuur 4 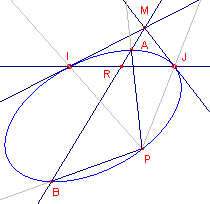abselem5 Voor de koorden IJ en AB geldt, dat de raaklijnen in I en J elkaar snijden het middelpunt M.
De punten I en J zijn de dubbelpunten van een involutie op de cirkel die wordt ingesneden door de koorden door M.
Daarnaast ligt de pool van IJ op AB.
De koorden zijn dus een elkaar toegevoegd.
Zij nu P een willekeurig punt van de cirkel. PI en PJ zijn dan dubbellijnen in de waaier met top P.

Klik hier Animatie voor een CabriJavapplet ter illustratie.

Uit de pooltheorie volgt dan dat P(IJAB) = -1. De lijnen PA en PB staan dus loodrecht op elkaar. ¨

Stelling 4
De middellijn door het midden van een koorde van een cirkel staat loodrecht op die koorde.

Bewijs:
figuur 5 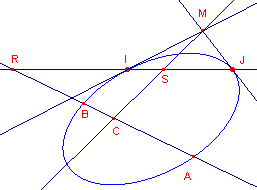abselem6 AB is een koorde. C is het midden van die koorden.
CM is de poollijn van R. CM snijdt l¥ in S.
Nu is (RSIJ) = -1.
Dus AB _|_ MC. ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.

Gevolg


Het middelpunt van de omcirkel van een driehoek ligt op de middelloodlijn van de zijde van die driehoek,
en ook
De middelloodlijnen van de zijden van de driehoek gaan door één punt (het middelpunt van de omcirkel).
[einde Gevolg]
Stelling 5
De raaklijn aan een cirkel staat loodrecht op de middellijn door het raakpunt.

Bewijs:
figuur 6 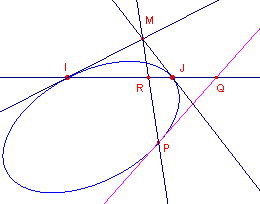abselem7 De raaklijn in P snijdt de oneigenlijke rechte in Q.
De middellijn door P snijdt de oneigenlijke rechte in R.
MP is de poollijn van Q.
Dus (RQIJ) = -1, waaruit volgt dat MP _|_ QP. ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.

3. Orthogonale cirkels terug
Omdat twee kegelsneden elkaar snijden in vier punten, snijden twee cirkels elkaars steeds in twee reële punten.
Stelling 6
Zijn P en Q de reële snijpunten van twee cirkels.
Het snijpunt van de raaklijnen in P en Q aan de ene cirkel ligt op de centraal (de verbindingslijn van de middelpunten) van beide cirkels, waarbij de centraal loodrecht staat op PQ.
.
figuur 7a figuur 7b

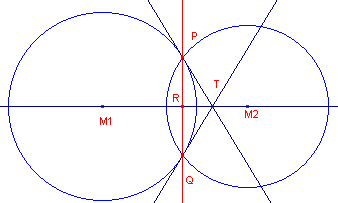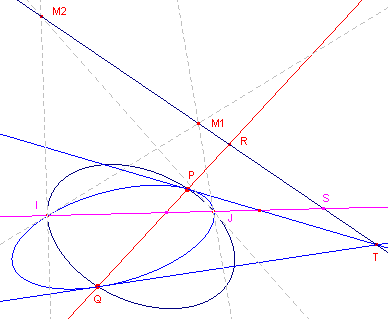abselem9		 abselem9b

Bewijs:


De raaklijnen in P en Q aan de cirkel met middelpunt M1 (zie figuur 7a en figuur 7b) snijden elkaar in T. T ligt dan op de loodlijn op PQ door M1. Hetzelfde geldt als we de raaklijnen in P en Q aan de andere cirkel bekijken.
T ligt dus op de lijn door de beide middelpunten. Dus M1M2 _|_ PQ. ¨
Stelling 7
Staan de raaklijnen aan twee elkaar in P snijdende cirkels loodrecht op elkaar, en is Q het tweede snijpunt van de cirkels, dan staan de raaklijnen aan beide cirkels in Q ook loodrecht op elkaar.

Bewijs:
figuur 8 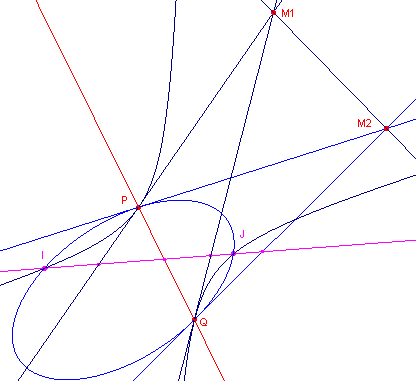abselem8 De raaklijn in P aan de cirkel met middelpunt M1 (in figuur 8 is deze weergeven als een ellips) is middellijn van de tweede cirkel (middelpunt M2; weergegeven als een hyperbool).
De raaklijnen in P en Q aan de cirkel M1 snijden elkaar dus in M2; de raaklijnen in P en Q aan cirkel M2 snijden elkaar in M1.
De raaklijn aan cirkel M1 in Q is dus middellijn van cirkel M2.
Dus staan de raaklijnen in P en Q aan cirkel M2 loodrecht op elkaar. ¨
.
Definities
[1]
Cirkels met de eigenschap dat de raaklijnen in een gemeenschappelijk punt loodrecht op elkaar staan, heten orthogonale cirkels.
[2]
Is CD een middellijn van een cirkel, dan heten de punten A en B op CD met (ABCD) = -1 inverse punten bij de cirkel met middellijn CD.
.
Stelling 8
[1]
Als twee cirkels orthogonaal zijn, dan snijdt elke middellijn van de ene cirkel de andere in een paar inverse punten
en omgekeerd
[2]
Als een cirkel door een paar inverse punten van de andere gaat, dan zijn de beide cirkels orthogonaal.

Bewijs:
figuur 9 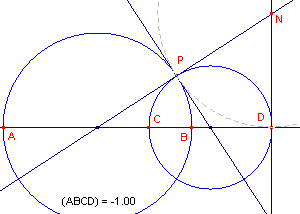abselem10 [1]
Zij CD een middellijn van de ene cirkel die de andere cirkel snijdt in de punten A en B.
Zij P een gemeenschappelijk punt van beide cirkels. Zij p de raaklijn in P aan cirkel PAB. De bundel cirkels die p in het punt P raken snijden de lijn AB in puntenparen van een involutie.
Nu staan de raaklijnen in P en D aan cirkel PCD staan loodrecht op opvolgend p en CD. Hun snijpunt is N. N is dan het middelpunt van een cirkel die p en CD in opvolgend P en D raakt.

Cirkel N behoort dus tot de bedoelde bundel. D is dan dubbelpunt van de genoemde involutie. Op dezelfde manier kan bewezen worden dat dit met C het geval is. A,B is dus een paar van die involutie. Daarom geldt (ABCD) = -1.
Per definitie zijn de punten A en B dan inverse punten bij de cirkel met middellijn CD. ¨

[2]


Zij P nu een gemeenschappelijk punt van beide cirkels. Er is precies één cirkel door A en P die orthognaal is met de cirkel PCD. Deze cirkel gaat door de 4e harmonische B van A, C en D. De gegeven cirkel gaat ook door B. Dus zijn de cirkels PAB en PCD orthogonaal. ¨

4. Cirkelbundels terug
figuur 10a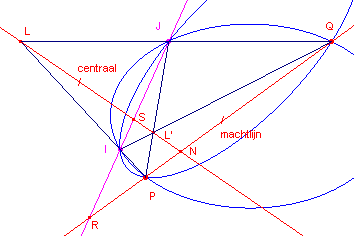

abselem11		 figuur 10b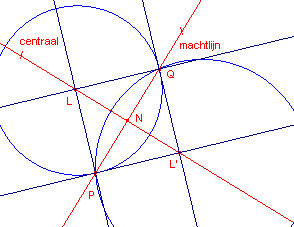

abselem11b

We beschouwen de verzameling cirkels die door de reële snijpunten P en Q van twee gegeven cirkels gaan.
Een dergelijke verzameling heet machtlijnsysteem.
De lijn PQ heet machtlijn van het systeem.
PI en QJ snijden elkaar in L; PJ en QI snijden elkaar in L’.
De punten L en L’ heten grenspunten van het systeem (ook wel punten van Poncelet genoemd).
Stelling 9
De middelpunten van de cirkels van een machtlijnsysteem liggen op de lijn door de grenspunten van het systeem.

Bewijs:


Zij R het snijpunt van de machtlijn met IJ. Driehoek LL’R is dan diagonaaldriehoek van de volledige vierhoek IJPQ.
Uit de pooltheorie volgt dan dat LL’R pooldriehoek is van alle kegelsneden door I,J, P en Q en dat zijn de cirkels van het systeem. IJ gaat door R (dat is de pool van LL’). Dus alle polen van de lijn IJ tov. de cirkels van het systeem liggen op LL’. ¨
Stelling 10
[1] De centraal van een machtlijnsysteem staat loodrecht op de machtlijn van het systeem.
[2] De centraal gaat door het midden van PQ.

Bewijs:


[1]
LL’ en PQ snijden IJ in punten die harmonisch liggen met I en J.
De centraal staat dus loodrecht op de machtlijn. ¨

[2]


Zij N het snijpunt van LL’ en PQ. Uit de theorie van de volledige vierhoek volgt nu, dat (PQRN) = -1.
N is dus per definitie het midden van PQ. ¨

Gevolg


PQ staat dus loodrecht op LL’.
Alle cirkels door L en L’ hebben hun middelpunt dus op PQ. Deze cirkels vormen een tweede machtlijnsysteem.
Daarbij zijn P en Q opvolgend de snijpunten van LI en L’J en van LJ en L’I.
De punten P en Q zijn dan de grenspunten van dit tweede machtlijnsysteem.
Er zijn dus steeds twee machtlijnsystemen; het ene heeft de punten L en L’ als grenspunten, het andere de punten P en Q.
En de machtlijn van het ene systeem is centraal van het andere.
Omdat LL’ elke cirkel door P en Q snijdt in punten die harmonisch gescheiden worden door L en L’, zijn de punten L en L’ inverse punten tov. deze cirkel.
Een cirkel uit het ene systeem staat dus loodrecht op een cirkel uit het andere systeem.
[einde Gevolg]

5. Concentrische cirkels terug
figuur 11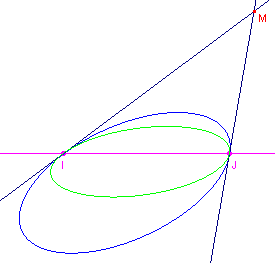

abselem12
Definitie
Cirkels met hetzelfde middelpunt heten concentrische cirkels.

Concentrische cirkels hebben dus gemeenschappelijke raaklijnen in de punten I en J.
Twee cirkels met hetzelfde middelpunt raken elkaar in I en J.
De lijn IJ (de oneigenlijke rechte) is dan dus machtlijn van het machtlijnsysteem.
De centraal van het systeem is ontaard in een punt, het punt M.
Bij een dergelijk systeem bestaat dus geen tweede machtlijnsysteem.

6. Hoogtepunt en rechte van Euler terug
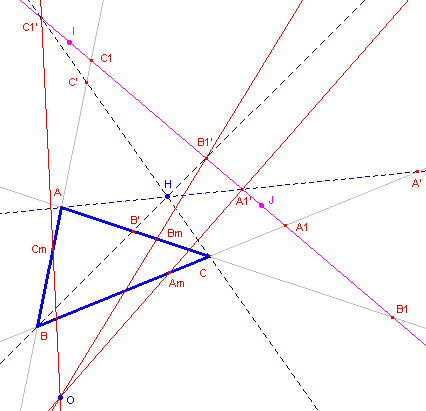
Stelling 11
[1] De hoogtelijnen van een driehoek gaan door één punt.
[2] De middelloodlijnen van een driehoek gaan door één punt.
[3] De zwaartelijnen van een driehoek gaan door één punt.

Bewijs:


[1] Zie figuur 12a.
figuur 12a 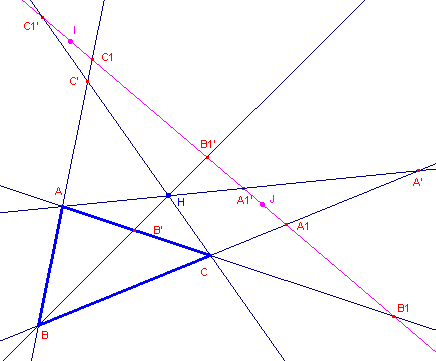abselem13 Zijn C1, A1 en B1, de oneigenlijke punten van de zijden van driehoek ABC.
Zijn C1’, A1’, B1’ de punten die daarmee harmonisch gescheiden liggen tov. de punten I en J.
De lijnen AA1’, BB1’, CC1’ zijn dan de hoogtelijnen van driehoek ABC.
De "voetpunten" van de hoogtelijnen zijn A’, B’ C’.
Zij nu H = AA’ /\ BB’.
De vier punten A, B, C en H vormen nu een volledige vierhoek. Twee paren overstaande zijden, te weten BC, AH en CA, BH snijden de lijn IJ in puntenparen van een involutie op de oneigenlijke rechte: (A1, A1’) en (B1, B1’).

Ook het puntenpaar bepaald door de lijnen AB en CH behoort nu tot die involutie.
Maar dat zijn de punten C1 en C1’. Waaruit volgt dat de lijnen AA’, BB’ en CC’ concurrent zijn in het hoogtepunt H. ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.

figuur 12b terug abselem13b [2]
Zijn Am, Bm, Cm de middens van de lijnstukken BC, CA en AB.
De lijnen AmA1’, BmB1’, CmC1’ zijn dan de middelloodlijnen van zijden BC, CA en AB.
Deze lijnen staan ook loodrecht op opvolgend de lijnen BmCm, CmAm en AmBm.
De middelloodlijnen gaan dus ook door één punt: het omcentrum O van de omcirkel van driehoek ABC (dit bewijs komt overeen met het traditionele bewijs van de concurrentie van de middelloodlijnen). ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.
figuur 12c terug abselem13c [3]
Zoals bekend (zie paragraaf 1, Gevolg van Stelling 1) gaan de zwaartelijnen AAm, BBm, CCm door één punt: het zwaartepunt Z van driehoek ABC. ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.
.
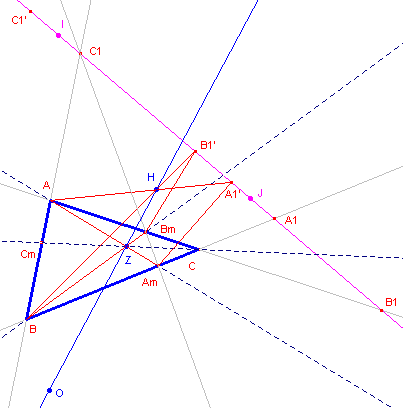
Stelling 12 (stelling van Euler)
De punten H, O en Z liggen op één lijn, de rechte van Euler van driehoek ABC.

Bewijs:

(zie figuur 12c)
Bekijk de driehoeken AAmA1’ en BBmB1’. Deze hebben een perspectivische ligging: AB, AmBm en A1’,B1’ zijn concurrent in het punt C1.
Volgens de stelling van Desargues zijn dan de punten H, O en Z collineair. ¨

7. Negenpuntscirkel terug
figuur 13 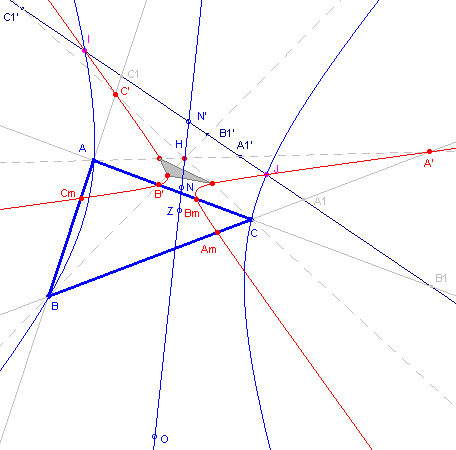abselem14 In figuur 13 is naast de omcirkel van driehoek ABC (de blauwe hyperbool) ook de Negenpuntscirkel of cirkel van Feuerbach (met middelpunt N) weergegeven (de rode hyperbool).
De grijze driehoek is de zogenoemde Euler-driehoek. De hoekpunten daarvan (de Euler-punten van de driehoek) zijn de middens van de lijnstukken AH, BH en CH.
De Negenpuntscirkel gaat door de middens van de zijden Am, Bm, Cm, door de voetpunten van de hoogtelijnen A’, B’, C’ en door de Euler-punten.
Het middelpunt N is het midden van het lijnstuk HO.

Klik hier Animatie voor een CabriJavapplet ter illustratie.

8. Download terug
De meeste figuren van deze pagina en de figuren die gebruikt zijn bij de CabriJavapplets, zijn in één bestand te downloaden via deze website.
Klik hier om het downloadproces te starten (ZIP-bestand, ca. 26Kb).

begin pagina

[abselem.htm] laatste wijziging op: 18-jan-18