Middelloodlijn, driehoeksongelijkheid, koordenvierhoek

Overzicht  ][  DK & meetkunde

Zie ook de pagina "Middelloodlijnen bij een vierhoek"

Overzicht terug

  1. Middelloodlijn
  2. Driehoeksongelijkheid
  3. Koordenvierhoek
  4. Stelling van tolemaeus

1. Middelloodlijn terug
Op deze pagina zullen we enkele meetkundige figuren behandelen, waarbij het begrip afstand een rol speelt.
Omdat we in de meetkunde (en niet alleen daar) graag willen weten wat we met een bepaald begrip bedoelen, geven we allereerst maar een definitie van het begrip afstand.

Definitie
Onder de afstand van twee punten A en B verstaan we de lengte van het lijnstuk AB.
We geven dit aan met d(A,B) of met |AB|.
Als er geen verwarring kan ontstaan met het lijnstuk AB zelf, of met de lijn door de punten A en B, kunnen we ook AB gebruiken.

Als eerste meetkundige figuur behandelen we de middelloodlijn van een lijnstuk.
We geven nog geen definitie, maar doen eerst een onderzoekje.
|§| Klik hier Animatie om dit onderzoek via een animatie te verrichten.

Op basis van het onderzoek leggen we nu het begrip middelloodlijn (zie figuur 1) vast:
Definitie
De middelloodlijn van lijstuk AB is de lijn die door het midden van het lijnstuk AB gaat en loodrecht op AB staat.

Uit het onderzoek blijkt de eigenschap die geformuleerd is in de volgende stelling.

Stelling 1
De verzameling van de punten P waarvoor geldt dat |PA| = |PB|, is de middelloodlijn van het lijnstuk AB.
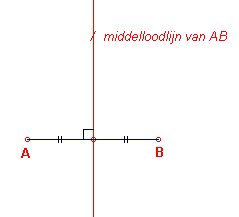figuur 1 imagesmidll1

Opmerkingen

  1. De begrippen verzameling en meetkundige plaats worden op deze webpagina's door elkaar gebruikt
  2. Als het woord verzameling in een meetkundige context verschijnt, moet bij bewijzen altijd "twee kanten op worden gekeken":
    • alle punten van de genoemde meetkundige figuur moeten de genoemde eigenschap(pen) hebben
    • alle punten met de genoemde eigenschap(pen) moeten tot de genoemde verzameling behoren

Dit is een gevolg van de definitie van gelijkheid van twee verzamelingen uit de algemene theorie der verzamelingen:
   ALS A en B twee verzamelingen zijn, DAN ( A = B) Û (A Ì B EN B Ì A).

[einde Opmerkingen]

We bewijzen nu stelling 1.
Bewijs:
(1) We weten: P ligt op de middelloodlijn van AB (zie figuur 2a)
We moeten nu bewijzen, dat PA = PB. We tekenen daartoe PA en PB. Uit de congruentie van de driehoeken APM en BPM (congruentiegeval ZHZ) volgt nu dat
  PA = PB.
(2) We weten nu: PA = PB.(zie figuur 2b)
We moeten nu bewijzen, dat P op de middelloodlijn ligt van AB. Teken de loodlijn uit P op AM. Deze snijdt AB in M. Uit de congruentie van de driehoeken APM en BPM (congruentiegeval ZZR) volgt dat AM = BM.
De getrokken loodlijn is dus de middelloodlijn van het lijnstuk AB. ¨

figuur 2a 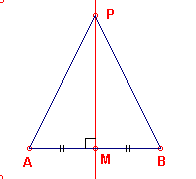imagesmidll2a      figuur 2b 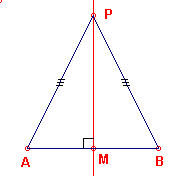imagesmidll2b      figuur 2c 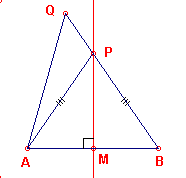imagesmidll2c

Opmerking
De tweede genoemde eigenschap ("alle punten met de genoemde eigenschap(pen) moeten tot de genoemde verzameling behoren") mogen we ook als volgt formuleren (volgens de zogenoemde logische omkering):
   Een punt dat niet tot de genoemde verzameling hoort, heeft de genoemde eigenschap(pen) niet.
[einde Opmerking]

We kijken nu naar figuur 2c.
Hier ligt het punt Q niet op de middelloodlijn van AB, maar aan dezelfde kant van de middelloodlijn als het punt A. Het lijnstuk BQ snijdt dan de middelloodlijn in het punt P. Omdat P op de middelloodlijn ligt geldt dat AP = BP.
We moeten nu dus aantonen, dat QA ¹ QB, dus dat QA < QB OF QA > QB.
Maar kunnen we dat met onze huidige kennis?

We kunnen echter onderzoek doen naar de ligging drie punten waarbij we letten op de afstanden tussen die punten.
|§| Klik hier Animatie om dit onderzoek via een animatie te verrichten.

2. Driehoeksongelijkheid terug
Uit het verrichte onderzoek formuleren we nu de zogenoemde driehoeksongelijkheid:

Stelling 2
Voor elk drietal punten A,B,P die niet op één lijn liggen geldt |AB| < |AP| + |BP|.
Als A,B,C collineair zijn, dan geldt |AB| = |AP| + |BP|

Of iets anders geformuleerd:
   In elke driehoek is de som van twee zijden groter dan de derde zijde.

En hiermee kunnen het afgebroken bewijs in de laatste opmerking van de vorige paragraaf afmaken (zie figuur 3).

figuur 3 imagesmidll2c In driehoek APQ is QA < AP + QP volgens stelling 2.
Maar dan is
  QA < BP + QP, immers AP = BP, zodat
  QA < QB ¨

Wat ons nu nog rest is een formeel bewijs van stelling 2.
Dit kan echter niet gegeven worden zonder dat we een andere stelling noemen (en bewijzen)..

Deze luidt:

Stelling 3
Zijn twee hoeken van een driehoek ongelijk, dan ligt tegenover de grootste van die hoeken een grotere zijde dan tegenover de kleinste.

We zullen nu, met behulp van deze stelling, de driehoeksongelijkheid bewijzen (zie figuur 4).

figuur 4 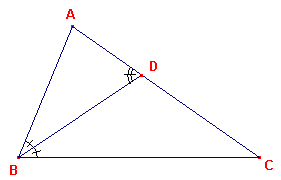imagesmidll3 In driehoek ABC tekenen we de bisectrice van hoek A die AC snijdt in het punt D. Nu geldt
ÐBDA = ÐDBC + ÐDCB (als buitenhoek van driehoek BCD; zie Elementen, prop. I-32). Dus,
ÐBDA > ÐDBC. Dus ook ÐBDA > ÐDBA, in driehoek BDA, waarop we stelling 3 toepassen:
   AB > AD ...(1)
Evenzo kunnen we aantonen, dat ÐBDC > ÐDBC, waaruit volgt
   BC > DC ...(2)
Tellen we (1) en (2) op dan vinden we AB + BC > AC
En hiermee is de driehoekongelijkheid bewezen. ¨

Klik hier voor het bewijs van stelling 3 en van de eigenschap van de buitenhoek van een driehoek, die in het bewijs van de driehoeksongelijkheid genoemd is..

3. Koordenvierhoek terug
Drie niet op één lijn gelegen punten bepalen een driehoek met drie zijden. Dus zijn er ook drie middelloodlijnen van die zijden. We bewijzen:

Stelling 4
De middelloodlijnen van de zijden van een driehoek gaan door één punt.

Bewijs:

In figuur 5 zijn de middelloodlijnen van de zijden AB en AC getekend. Het snijpunt daarvan is het punt O.
Omdat O ligt op de middelloodlijn van AB, geldt OA = OB.
Omdat O ligt op de middelloodlijn van AC, geldt OA = OC.
Dus OB = OC.
Volgens stelling 1 volgt hieruit dat O op de middelloodlijn van BC ligt. De drie middelloodlijnen gaan dus door één punt. ¨		    figuur 5 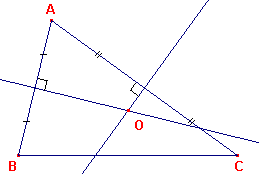imagesmidll4

Opmerking
Het punt O is het middelpunt van de omgeschreven cirkel van driehoek ABC
[einde Opmerking]

We vragen ons nu af wat er gebeurt als we een vierde punt toevoegen. We gaan dan dus uit van vier punten en 3+2+1 = 3+3 = 6 middelloodlijnen.
Zie eventueel ook de pagina "Middelloodlijnen bij een vierhoek".
|§| Klik hier Animatie om dit onderzoek via een animatie te verrichten.

We hebben dus gezien dat, als de vier punten op een cirkel liggen, de middelloodlijnen van de zes lijnstukken door één punt gaan.

figuur 6a 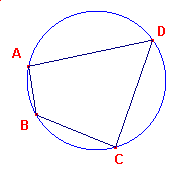imagesmidll5      figuur 6b 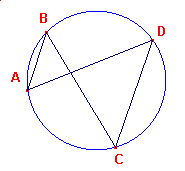imagesmidll6

De ligging van de punten A, B, C, D op de cirkel heeft tot gevolg dat de zijden van vierhoek ABCD koorden van die cirkel zijn (zie figuur 6a en figuur 6b).
De ligging zoals aangegeven in figuur 6b zullen we in hetgeen volgt niet bekijken; in dit geval is ABCD niet-convex; twee zijden van de vierhoek snijden elkaar inwendig.

Definitie
Een convexe vierhoek heet koordenvierhoek als de hoekpunten op één cirkel liggen.

Voor een koordenvierhoek zullen we een eigenschap voor de vier hoeken bewijzen. We formuleren deze eigenschap in de volgende stelling.

Stelling 5
In elke koordenvierhoek ABCD geldt ÐA + ÐC = ÐB + ÐD = 180º.

1e Bewijs:
We verbinden de hoekpunten met het middelpunt M van de omgeschreven cirkel van de koordenvierhoek (zie figuur 7a, b).
Merk op dat er voor het punt M drie verschillende mogelijkheden zijn: M binnen de vierhoek, M op de verhoek en M buiten de vierhoek
Dan is MA = MB = MC = MD. Als M binnen of buiten de vierhoek ligt, is de vierhoek is verdeeld in 4 gelijkbenige driehoeken.

figuur 7a 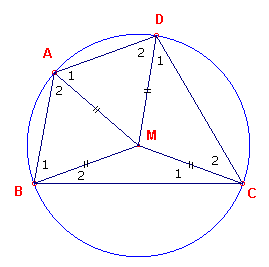imagesmidll7      figuur 7b 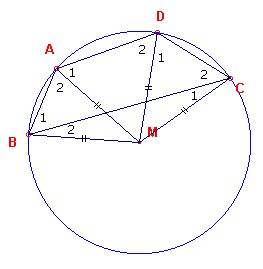imagesmidll8

Nu is:

(figuur 7a) ÐA + ÐC  = ÐA12 + ÐC12
= ÐA1 + ÐA2 + ÐC1 + ÐC2
= ÐD2 + ÐB1 + ÐB2 + ÐD1
= ÐB + ÐD		     In het geval dat M op de vierhoek ligt, is ÐB2 = ÐC1 = 0º.
(figuur 7b) ÐA + ÐC = ÐA12 + ÐC2
= ÐA1 + ÐA2 + (ÐC12 - ÐC1)
= ÐD2 + (ÐB1+ÐB2) + ÐD1 - ÐB2
= ÐB + ÐD

Aangezien we weten, dat in een vierhoek de hoekensom 360º is, hebben we dus ÐA + ÐC = ÐB + ÐD = 180º. ¨

2e Bewijs:
Als we gebruik maken van hoeken waarvan de hoekpunten op de omtrek van een cirkel liggen (zie Elementen, Propositie III-20), dan hebben we in figuur 7a:
   ÐA + ÐD = ½bg(BCD) + ½bg(DAB) = ½ 360º = 180º, en
   ÐB + ÐD = ½bg(ADC) + ½bg(CBA) = ½ 360º = 180º. ¨

Opmerking
Het tweede bewijs komt overeen met het bewijs van deze stelling in de Elementen van Euclides, te weten in Boek III, als propositie 22 (zie 3e bewijs).
Deze plaats in boek III is niet verwonderlijk, omdat de propositie bijna onmiddellijk volgt op de propostie (Elementen, prop. III-20) die luidt
   In een cirkel is een hoek aan het middelpunt het dubbele van een hoek aan den omtrek, wanneer de hoeken denzelfden boog als de basis hebben.
[einde Opmerking]

3e Bewijs:
Klik hier voor het in de Elementen staande bewijs van stelling 5.

Voor de omgekeerde stelling van stelling 5 kiezen we een andere benadering dan misschien verwacht.
|§| Klik hier Animatie om deze benadering via een animatie te bekijken.

De animatie geeft een illustratie van de omgekeerde stelling van stelling 5. Deze omgekeerde stelling formuleren we wat uigebreider.

Stelling 6
(1) Als voor de vierhoek ABCD geldt ÐB + ÐD = 180º, dan is ABCD een koordenvierhoek.
(2) Als voor de vierhoek ABCD geldt ÐB + ÐD > 180º, dan ligt B binnen de omgeschreven cirkel van driehoek ACD
(3) Als voor de vierhoek ABCD geldt ÐB + ÐD < 180º, dan ligt B buiten de omgeschreven cirkel van driehoek ACD.

Natuurlijk is met de animatie deze stelling nog niet bewezen.

Bewijs van (1): (zie figuur 8)

Teken de omgeschreven cirkel van driehoek ACD. We zullen bewijzen, dat B hierop ligt.
Kies het punt B' op de boog DAE en trek AC.
Nu is dus AB"CD een koordenvierhoek. Dus ÐB' + ÐD = 180º. Of
   ÐB' = 180 - ÐD
Uit het gegeven, ÐB + ÐD = 180º, volgt echter
   ÐB = 180º - ÐD.
Dus
   ÐB' = ÐB
Het lijnstuk AC wordt vanuit B en B' onder gelijke hoeken gezien. B en B' liggen dus (*) op dezelfde boog.
Met andere woorden ook B' ligt op de omgeschreven cirkel van ACD. ¨		      figuur 8 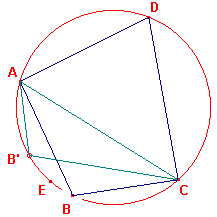imagesmidll9

(*) Klik hier voor het bewijs van deze eigenschap, die het gevolg is van Elementen, boek III, propositie 21.

Bewijs van (2) en (3):
We bewijzen dit met behulp van de logische omkering. De logische omkering van
(2) Als voor de vierhoek ABCD geldt ÐB + ÐD > 180º, dan ligt B binnen de omgeschreven cirkel van driehoek ACD
is
Als B niet binnen de omgeschreven cirkel van driehoek ACD ligt, dan is ÐB + ÐD £ 180º

We kunnen dus van twee gevallen uitgaan ("B niet binnen" betekent:)

   (i)   B ligt op de omgeschreven cirkel van driehoek ACD;
   (ii)  B ligt buiten de omgeschreven cirkel van driehoek ACD.
figuur 9 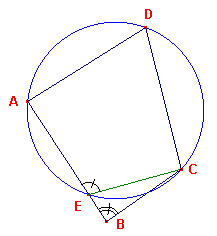imagesmidll10     
(i) Als B op de omgeschreven cirkel van driehoek ACD, dan is ÐB + ÐD > 180º; dus ÐB + ÐD £ 180º is juist.

(ii) We nemen nu B buiten de omgeschreven cirkel van driehoek ACD
In dit geval snijdt het lijnstuk AB de omgeschreven cirkel van driehoek ADC in het punt E (zie figuur 9).
Verbinden we nu E met C, dan is hoek E een buitenhoek van driehoek EBC en AECD is een koorden vierhoek. Zodat
   ÐE = ÐB + ÐC (beide laatste in driehoek EBC).
Tellen we nu hD van de koordenvierhoek hierbij, dan is
   ÐE + ÐD = 180º = ÐB + ÐC + ÐD.
Met andere woorden
   ÐB + ÐD < 180; ook in dit geval is dus ÐB + ÐD £ 180º juist.
Hiermee is stelling 6 dus geheel bewezen.¨

4. De stelling van Ptolemaeus terug
Deze stelling zegt ook iets over een koordenvierhoek, en wel over de zijden en de diagonalen.

Stelling 7
In een koordenvierhoek is de som van de producten van lengtes van de paren overliggende zijden is gelijk aan het product van de lengtes van de diagonalen.

Klik hier voor een bewijs van deze stelling, waarmee ook de somformule voor sin(p + q) kan worden afgeleid.

begin pagina
[middello.htm] laatste wijziging op: 27-12-03