Hyperbolische functies

Pagina-overzicht  ][ Analyse  |  Hyperbolische meetkunde

0. Overzicht

  1. Cirkelfuncties
  2. Hyperboolfuncties
         2.1. Definities
         2.2. Eigenschappen
         2.3. Grafieken
  3. Hyperbooltrapezium
         3.1. De functie ln(x)
         3.2. De vergelijking x2 - y2 = 1 wordt xy = ½
         3.3. Verband tussen de oppervlakte van een hyperbooltrapezium en een hyperboolsegment
  4. Hyperbolische functies met e-machten
  5. Inverse hyperbolische functies

1. Cirkelfuncties
De sinus, cosinus en tangens worden gedefinieerd met behulp van een cirkel met straal 1 (eenheidscirkel).
Voor deze definities en het verband tussen booglengte (op de cirkel) en deze functies wordt verwezen naar de pagina "Sinus, cosinus en tangens als functies".

figuur 1 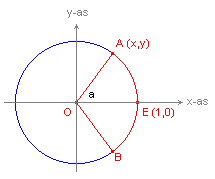hypfunc1 We kunnen ook een verband leggen tussen deze functies en de oppervlakte van sectoren van de eenheidscirkel.
In figuur 1 hebben we:
- A (x,y)
- B( x,-y)
- E (1,0)
- de hoek AOE = a (in radialen, cq. reëel).

Nu is de oppervlakte U van de sector OAB = (2a)/(2p) . p = a, zodat
   x = cos a = cos U
   y = sin a = sin U
   y/x = tan a = tan U

Aanvullende afspraak
We maken hierbij nog een afspraak over het teken van de oppervlakte U.
We rekenen U positief als de y-coördinaat van A positief is.U is negatief als de y-coördinaat van A negatief is.

Opmerking
Voor alle punten met coördinaten (x,y) op de eenheidscirkel geldt x2 + y2 = 1.
[einde Opmerking]

2. Hyperboolfuncties
2.1. Definities
We bekijken nu de verzameling punten met coördinaten (x,y) die voldoen aan de vergelijking x2 - y2 = 1 (met x ³ 1).
Deze punten liggen op de rechts van de y-as gelegen deel van een orthogonale hyperbool (zie figuur 2).

figuur 2 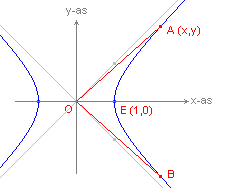hypfunc2

Op dezelfde manier als bij de cirkelfuncties, maar nu per definitie, hebben we:

Definitie
Zij U de oppervlakte van de hyperboolsector OAB van de orthogonale hyperbool x2 - y2 = 1, waarbij A(x,y) en B(x,-y).
Dan is:
cosinus hyperbolicus: x = cosh U
sinus hyperbolicus: y = sinh U
tangens hyperbolicus: y/x = tanh U

We schrijven ook wel ch, sh en th.
Ook hier kennen we aan U een teken toe: positief als de y-coördinaat van A positief is; negatief als de y-coördinaat negatief is.

2.2. Eigenschappen
Gemakkelijk is nu in te zien, dat
- cosh2 U - sinh2 U = 1
- tanh U = sinh(U) / cosh(U)

Verder is
[1]
sinh(-U) = oppervlakte (OBA) = - oppervlakte (OAB) = - sinh (U)
omdat de y-coördinaten van teken wisselen.
[2]
cosh(-U) = oppervlakte (OBA) = oppervlakte(OAB) = cosh(U)
omdat de x-coördinaten niet van tekenwisselen.
[3]
tanh(-U) = sinh(-U) / cosh(_U) = -sinh(U) / cosh(U) = -tanh(U)
De functies sinh en tanh zijn dus oneven fucnties; cosh is een even functie.

2.3. Grafieken
In figuur 3 zijn de grafieken van de hyperbolische functies getekend.

figuur 3 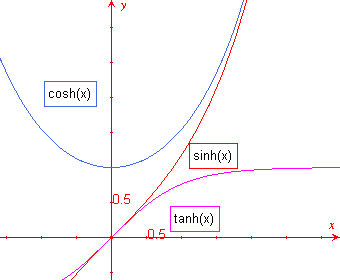hypfunc3 Voor de inverse functies zie figuur 8.

3. Hyperbooltrapezium
3.1. De functie ln(x)

figuur 4 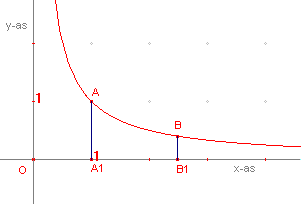hypfunc4 In figuur 4 is getekend de grafiek van de functie 
   f(x) = 1 / x (voor x > 0).
Op de grafiek van deze functie liggen de punten A(1,1) en B(t, 1/t).
De projecties van A en B op de x-as zijn A1 en B1.
We noemen nu de figuur begrensd door de lijnstukken AA1, A1B1, B1B en het deel AB van de grafiek van f een hyperbooltrapezium.

We kunnen nu de oppervlakte van dit hyperbooltrapezium (volgens de integraalrekening) schrijven als
   hypfuncf1
waarbij we B1 nu dus de coördinaten (x,0) geven.
We kunnen nu bewijzen (niet hier) of definiëren:
  hypfuncf2     voor x > 0
De functie ln(x) noemen we de natuurlijke logaritme van x.
Deze functie heeft ondermeer de volgende eigenschappen:
   ln(ab) = ln(a) + ln(b)
   ln(a/b) = ln(a) - ln(b)
Verder is
   ln(a) = b equivalent met e b = a.
De functie ln(x) is dus de inverse functie van de functie ex (voor het getal e zie ook de pagina "De functie ax en het getal e").

3.2. De vergelijking x2 - y2 = 1 wordt xy = ½
We roteren de grafiek van de relatie x2 - y2 =1 over een hoek van 45° in positieve richting.
Daardoor vallen de asymptoten samen met de x- en y-as. Het punt A gaat daardoor over in A' (zie figuur 5) met coördinaten (x', y').
We bepalen het verband tussen x' en y'.

figuur 5 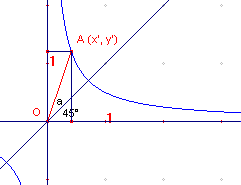hypfunc5 Nu is:
x' = cos(45° + a) OA = ½Ö2(cos a - sin a) OA
y' = sin(45° + a) OA = ½Ö2(cos a + sin a) OA
Vermenigvuldiging geeft dan
x'y' = ½(cos2 a - sin2 a)OA2 = ½(cosh2 U - sinh2 U) = ½

De vergelijking van de geroteerde orthogonale hyperbool is dus
     xy = ½

3.3. Verband tussen de oppervlakte van een hyperbooltrapezium en een hyperboolsegment

figuur 6 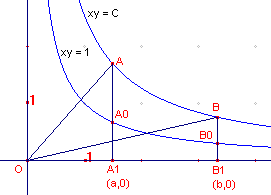hypfunc6 In figuur 6 zijn getekend de orthogonale hyperblen
   xy = C
   xy = 1
De punten A en B liggen willekeurig op xy = C.
Nu is de oppervlakte van het hyperbooltrapezium A1B1B0A0 gelijk aan
   ln(b) - ln(a) = ln(b/a)
De oppervlakte van het hyperbooltrapezium A1B1BA is dan gelijk aan
   C ln(b/a)
vanwege de verticale lijnvermenigvuldiging met factor C.

In verband met de ligging van A en B op de hyperbool xy = C hebben we verder
   OA1 . A1A = OB1 . B1B ( = C)
De oppervlaktes van de driehoeken OAA1 en OBB1 zijn dus aan elkaar gelijk.
Door optelling van de oppervlakte van OAA1 bij die van het hyperbooltrapezium en aftrekking van de oppervlakte van driehoek OBB1 vinden we dat
   Opp(hyperboolsector OAB) = Opp(hyperbooltrapezium A1B1BA)
Dus
   Opp(hyperboolsector OAB) = C ln(b/a)

4. Hyperbolische functies met e-machten

figuur 7 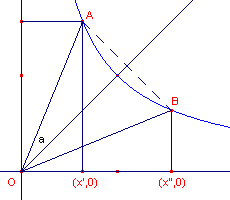hypfunc7 We leiden nu uitdrukking voor de hyperbolische functies af met e-machten.
In figuur 7 hebben we de hyperboolsector getekend op de hyperbool met vergelijking xy = ½.
Voor de coordinaten x' en x" geldt nu weer:
   x' = cos(45° + a)OA = ½Ö2(cos a - sin a) = ½Ö2(x - y)
   x" = sin(45° + a)OA = ½Ö2(cos a + sin a) = ½Ö2(x + y)
x en y zijn hierin de "oude" coördinaten van het punt A (dus voor de hyperbool x2 - y2 = 1).
Volgens de laatste formule in paragraaf 3.3 is nu
   U = Opp(hyperboolsector OAB) = ½ ln( (x+y)/(x-y) )

Hieruit volgt dan:
(4.1)....hypfuncf3
Maar x2 - y2 = 1 geeft
(4.2) ..... (x + y)(x - y) = 1
Vermenigvuldiging van (4.1) en (4.2) levert
               (x + y)2 = e 2U
en dus
               x + y = e U
               x - y = e-U
Door optelling en aftrekking vinden we uitdrukkingen van x ( = cosh U) en  y ( = sinh U)  in machten van e, zodat

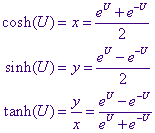
   hypfuncf4

Opmerking
De hyperbolische functies zijn voor het eerst geïntroduceerd door Vincenzo Riccati, 1707-1775, Italië.
[einde Opmerking]

5. Inverse hyperbolische functies
De inverse functies van de hyperbolische functies worden genoteerd als arcosh of arch (area cosinus hyperbolicus), arsinh of arsh (area sinus hyperbolicus) en artanh of arth (area tangens hyperbolicus).
"Area" betekent hierin "oppervlakte".

figuur 8 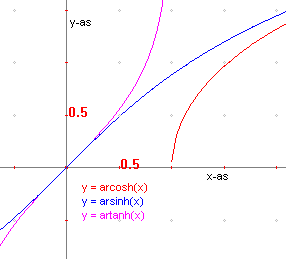hypfunc8 Vergelijk deze functies met die in figuur 3.

begin pagina

[hypfunc.htm] laatste wijziging op: 28-09-2003