Sinus, cosinus en tangens als functies Goniometrische functies Overzicht ][ DK & Analyse
Zie ook de pagina "Cyclometrische
functies"
Zie ook de pagina "Over de secans en cosecans"
- Sinus-functie

- Cosinus-functie

- Tangens-functie

- Eigenschappen
4.1. Goniometrische verhoudingen en goniometrische functies
4.2. Enkele eigenschappen van de sinus-functie
4.3. Enkele eigenschappen van de cosinus-functie
4.4. Enkele eigenschappen van de tangens-functie
4.5. Stelling van Pythagoras voor de goniometrie - Functiewaarden

- Vreemde woorden
- Afgeleiden
1.
Sinus-functie ![]()
We gaan uit van een cirkel met straal 1 waarvan het middelpunt op de x-as ligt (eenheidscirkel).
De omtrek van de cirkel is dus gelijk aan 2p.
Op de cirkel kiezen we een punt A dat tegen de wijzers van de klok in over de
cirkel beweegt. Het startpunt van A is het punt O (zie figuur 1).
We kiezen nu een punt X op de x-as waarvoor geldt dat OX = lengte van de boog OA.
Het punt X legt daardoor op de x-as dezelfde afstand af, als het punt A op de
cirkel.
| figuur 1 | 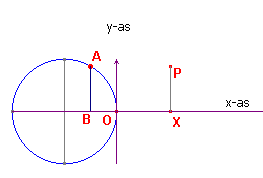 |
We meten nu de afstand van het punt A tot de horizontale middellijn van
de cirkel. Dat is dus de lengte van het lijnstuk AB, waarbij we de afstand negatief rekenen als A onder de horizontale middellijn ligt. P is nu het punt waarvan de x-coördinaat gelijk is aan die van het punt X en waarvan de y-coördinaat gelijk is aan AB (inclusief het teken). Het punt P beschrijft nu een kromme lijn, een zogenoemde sinusoïde. |
Dit is de grafiek van de functie f(x) = sin x.
Klik hier ![]() voor een animatie
van het bovenstaande.
voor een animatie
van het bovenstaande.
We hebben dus gevonden voor waarden van x tussen 0 en 2p:
| figuur 2a | 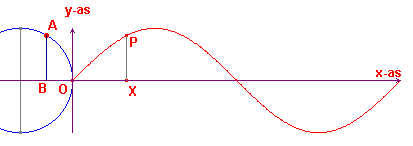 |
We breiden het domein van de sinusfunctie uit tot alle reële waarden van x door de
functie periodiek te maken.
Een dergelijke uitbreiding verkrijgen we door de definitie
sin(x + k . 2p) = sin x voor k = ±1, ±2, ±3, ...
Het getal 2p heet de periode van de functie.
De grafiek van sin x heeft daardoor dus de volgende gedaante
| figuur 2b | 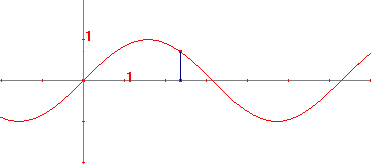 |
f(x) = sin x |
| figuur 3 | 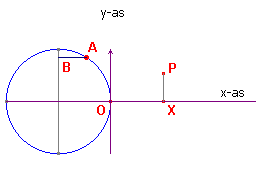 |
Voor het verkrijgen van de functie cos x gaan we op
dezelfde manier te werk als bij de sinusfunctie. Echter nu nemen we voor AB de afstand van het punt A tot de verticale middellijn van de cirkel. Daarbij kiezen we deze afstand positief als A rechts van die middellijn ligt en negatief als A er links van ligt (zie figuur 3). In dit geval beschrijft het punt P ook een kromme lijn. Deze is gelijkvormig met die welke we gevonden hebben bij de sinusfunctie. Het is dus eveneens een sinusoïde. |
Het is in dit geval echter de grafiek van de functie f(x) = cos x.
Klik hier ![]() voor een animatie
van deze functie.
voor een animatie
van deze functie.
Hier vinden we dus, eveneens voor waarden van x tussen 0 en 2p:
| figuur 4a | 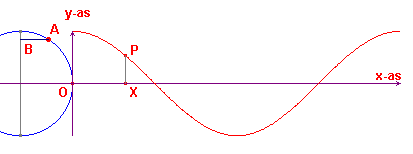 |
Ook van deze functie breiden we het domein uit tot alle reële getallen met
cos(x + k . 2p) = cos x voor k = ±1, ±2, ±3, ...
De cosinus-functie is dus eveneens een periodieke functie. Het getal 2p heet de periode van de functie.
Daardoor heeft de grafiek van cos x de volgende gedaante:
| figuur 4b | 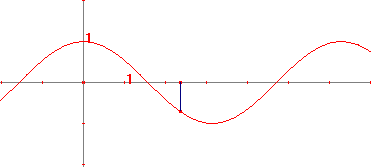 |
f(x) = cos x |
Opmerking
De sin-functie en de cos-functie behoren tot de verzameling zogenoemde goniometrische
functies.
[einde Opmerking]
3.
Tangens-functie ![]()
Naast de sin- en cos-functie definiëren we op dezelfde manier als hierboven nog een derde
goniometrische functie, nl. de tangens-functie of kortweg de tan-functie.
| figuur 5 | 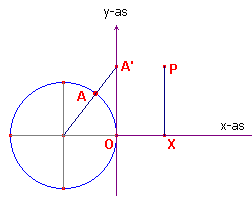 |
We trekken nu een lijn door het middelpunt van de eenheidscirkel
en het variabele punt A. Deze lijn snijdt de yas in het punt A'. Als y-coördinaat
van het punt P nemen we dit keer de lengte van het lijnstuk A'O. Als A' boven de x-as ligt
nemen we de positieve waarde; ligt A' daarentegen onder de x-as dan kiezen nemen we de y-coördinaat
negatief. Ook nu beschrijft het punt P een kromme lijn (dit is echter geen sinusoïde!).. |
Dit is de grafiek van de functie f(x) = tan x.
Klik hier >![]() <
voor een animatie van deze functie.
<
voor een animatie van deze functie.
We hebben dus gevonden voor waarden van x tussen 0 en 2p:
| figuur 6a | 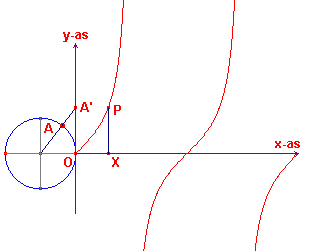 |
Merk echter op, dat voor de waarden x = ½p (A
heeft een kwart cirkel doorlopen) en x=1½p (A heeft driekwart
cirkel doorlopen) de lijn door het middelpunt en A evenwijdig loopt met de y-as.
In dit geval bestaat het punt A' dus niet.
De tan-functie is niet gedefinieerd voor de waarden x = ½p en x=1½p.
Ook van de tan-functie breiden we het domein uit voor alle reële waarden van x. Dit keer met
tan(x + k . p) = tan x voor k = ±1, ±2, ±3, ... en uiteraard x + k . p ¹ ½p en ¹ 1½p.
De tangens-functie is dus een periodieke functie met een periode gelijk aan p.
Daardoor heeft de grafiek van tan x de volgende gedaante:
| figuur 6b | 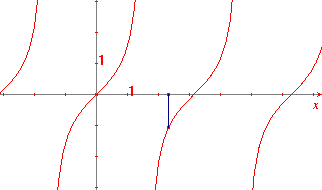 |
f(x) = tan x |
4.
Eigenschappen ![]()
4.1. Verband tussen goniometrische verhoudingen en
goniometrische functies ![]()
We zullen hieronder nagaan welk verband er bestaat tussen
de goniometrische verhoudingen die gedefinieerd zijn in een rechthoekige driehoek en de
hierboven besproken functies.
Deze goniometrische verhoudingen, die dezelfde namen hebben als de beschouwde functies,
geven we aan met SIN, COS en TAN.
| figuur 7 | 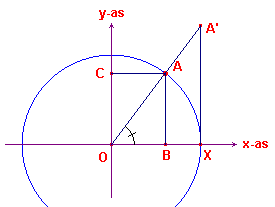 |
In figuur 7 is de eenheidscirkel getekend met middelpunt O. De omtrek van de cirkel is dus 2p. A is een punt van deze cirkel. We stellen de grootte van hoek AOX gelijk aan x (radialen). Nu is de lengte van boog AX gelijk aan x/2p . 2p = x. In driehoek AOB is nu SIN x = AB/OA = AB/1 = AB |
In de functies hebben we de lijnstukken AB, AC en A'X opvolgend gebruikt als
functiewaarden voor de sinus, cosinus en tangens.
Dus voor waarden van x uit het interval [0, ½p]
geldt:
SIN x = sin x
COS x = cos x
TAN x = tan x
De goniometrische verhoudingen en de goniometrische functies geven dus voor scherpe hoeken
bij O dezelfde waarden.
Ook voor andersoortige hoeken (A ligt dan in het 2e, 3e of 4e kwadrant van de cirkel)
kunnen we goniometrische verhoudingen definiëren.
We doen dat met behulp van de coördinaten (p, q) van het punt A op
de eenheidscirkel.
| Definitie Als de grootte van de hoek AOX gemeten wordt over de boog die XA in tegenwijzerrichting waarbij bg(XA) = x, dan is SIN AOX = q COS AOX = p TAN AOX = q / p |
Uit deze definities dat ook nu steeds geldt
SIN x = q = sin x
COS x = p = cos x
TAN x = q/p = tan x
Hieruit volgt tevens, dat tan x = sin x / cos x.
4.2. Enkele eigenschappen van de sinus-functie ![]()
| figuur 8a | 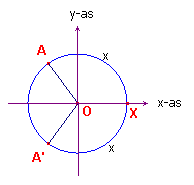 |
Zie figuur 8a. Hierin is bg(XA) = x. Omdat A' gekozen is als spiegelbeeld van A in de x-as is ook bg(XA') = x. Daardoor is bg(XAA') = 2p - x. Nu is
Dus: sin(- x) = - sin x |
||||
| figuur 8b | 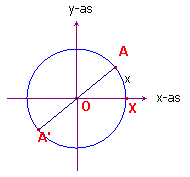 |
Zie figuur 8b. Hierin is bg(XA) = x. Omdat A' gekozen is als spiegelbeeld van A in het punt O is bg(XAA') = x + p. Nu is sin(x + p) = - sin x Verder is sin(x + p) = sin(x + p - 2p) = sin(x - p) = - sin x Dus: sin(x ± p) = - sin x. |
4.3. Enkele eigenschappen van de
cosinus-functie ![]()
| figuur 9a | 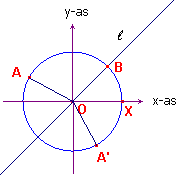 |
Het punt B komt overeen met x = ¼p. Verder is bg(BA) = a. Het punt A komt dus overeen met x = ¼p + a. Het punt A' is het spiegelbeeld van A in de lijn l. Het punt A' komt dus overeen met x = 2¼p - a Nu is y(A) = x(A'),
dit volgt uit de spiegeling, zodat
|
||||
| figuur 9b |  |
Zie figuur 9b. Voor het punt A geldt x(A') = x(A), terwijl verder bg(XAA') = 2p - x. Dus cos(2p -x ) = cos(-x) = cos x We hebben dus gevonden cos(-x) = cos x |
||||
| figuur 9c |  |
Zie figuur 9c. Hierin is bg(XA) = x. Omdat A' gekozen is als spiegelbeeld van A in het punt O is bg(XAA') = x + p. Nu is cos(x + p) = - cos x Verder is cos(x + p) = cos(x + p - 2p) = cos(x - p) = - cos x Dus: cos(x ± p) = - cos x. |
4.4. Een eigenschap van de tangens-functie
![]()
Door gebruik te maken van de onder 3 genoemde eigenschap van de tangens-functie, tan x = sin x / cos x,
kunnen we eenvoudig via de eigenschappen van de sinus- en cosinus-functie layen zien, dat
tan(- x) = - tan x
Immers, tan(-x) = sin(-x) / cos(-x) = - sin x / cos x = - tan x.
4.5. Stelling van Pythagoras voor de
goniometrie ![]()
| figuur 10 | 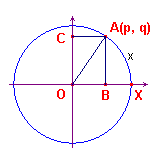 |
Voor elk punt A (p, q) van de eenheidscirkel geldt dat p
= cos x en q = sin x, waarbij bg(XA) = x. Zie figuur 10. Voor de afstand van A tot O geldt dus volgens de stelling van Pythagoras, dat p2 + q2 = 1; zodat sin2x + cos2x = 1 |
5.
Functiewaarden ![]()
In het volgende overzicht staan enkele belangrijke functiewaarden voor de goniometrische
functies en de tekens van de functieaarden voor x in de verschillende kwadranten.
| Tabel van functiewaarden en tekenoverzicht | ||||||||||||
| x = (in radialen) | 0 | 1/6p | 1/4p | 1/3p | 1/2p | |||||||
| x = (in graden) | 0 | 30 | 45 | 60 | 90 | x in kwadrant | I | II | III | IV | ||
| sin x | 0 | 1/2 | 1/2 Ö2 | 1/2 Ö3 | 1 | sin x | + | + | - | - | ||
| cos x | 1 | 1/2 Ö3 | 1/2 Ö2 | 1/2 | 0 | cos x | + | - | - | + | ||
| tan x | 0 | 1 / Ö3 | 1 | Ö3 | ? | tan x | + | - | + | - | ||
De waarden kunnen worden afgeleid met behulp van de stelling van Pythagoras een
driehoek met hoeken van 45, 45 en 90 graden en in een driehoek met hoeken van 30, 60 en 90
graden.
De tekens volgen onmiddellijk uit de definities van de functies.
![]()
Klik hier >![]() < voor een Cabri-applet
die voor hoeken tussen 0º en 360º de waarden van de sinus, cosinus
en tangens geeft (Nb. Cabri Plus Plug-in
vereist!).
< voor een Cabri-applet
die voor hoeken tussen 0º en 360º de waarden van de sinus, cosinus
en tangens geeft (Nb. Cabri Plus Plug-in
vereist!).
6. Vreemde woorden ![]()
In ' Vreemde woorden in de wiskunde' (Dr. E.J. Dijksterhuis, P.
Noordhof, 1948) vinden we:
Sinus (Lat. = plooi, bocht, boezem). In de Indische wiskunde heette de helft van de koorde van het dubbele van een cirkelboog de ardhâ-jyâ (ardha = half; jyâ = koorde) van dien boog. Dit werd, afgekort tot jyâ of jîv, door de Arabieren als vgîb geschreven en wegens overeenstmming in de alleen neergeschreven consonaten geidentificeerd met Arab. vgaib = plooi of opening van een kledingstuk; fig. boezem. Dit werd daarna in het Lat. lett. vertaald als sinus. Deze vertaling komt het eerst voor bij Gerard van Cremona (1114-1187). Mv. sinussen.
Cosinus. Afkorting voor complimenti sinus = sinus van het complement. Mv. cosinussen.
Tangens (sc. linea = raaklijn; Lat. part. praes. van tangere = raken). Eerst in de 16e eeuw wordt het woord ook gebruikt voor een goniometrische functie. Deze heette voor dien tijd umbra versa of umbra stans (gedraaide of staande schaduw). Zij werd namelijk beschouwd als de schaduw, die een lichtend punt in het middelpunt van een cirkel van een sinus op de daaraan evenwijdige raaklijn werpt. Dat zij « gedraaide schaduw » heette, kwam hieruit voort, dat de naam umbra reeds in gebruik was voor de horizontale schaduw, die de zon van een verticaal geplaatste staaf werpt (de cotangens van de hoogte). Mv. tangenten.
7. Afgeleiden ![]()
Voor de afgeleiden van de functies sin, cos en tan zie het artikel
"Over de afgeleide van de
functie sin(x)" (PDF-bestand, ca. 60Kb).