Cyclometrische functies
Overzicht ][ Goniometrische functies | Analyse
- Inleiding
- Cyclometrische functies
2.1. Sinus en arcsin
2.2. Cosinus en arccos
2.3. Tangens en arctan - Afgeleiden
- Eigenschappen
1. Inleiding:
inverse functie 
Een functie f is niets meer dan een voorschrift dat aan ieder element x
van een verzameling (het domein) D precies één element y van een
verzameling (het codomein of bereik) B toevoegt.
Daarbij is het niet uitgesloten, dat aan twee (of meer) verschillende elementen van D
hetzelfde element van B wordt toegevoegd.
Voorbeeld
y = f(x) = x² met D = [-1, 1]
Is echter ieder element y van B het beeld van precies één
element x van D, dan is door het geven van zo'n y het origineel
x van D eenduidig bepaald.
We kunnen dan eveneens spreken van een functie g(y) = x.
De functie g noemen we de inverse functie van f. We
noteren die als f inv.
Er zijn geen algemene voorwaarden op te stellen voor de eis dat een willekeurige
functie een inverse heeft.
Er geldt echter wel de volgende stelling (hier verder niet bewezen):
| Stelling Als f een functie is die gedefinieerd is op [a, b] en daar monotoon stijgt (daalt), terwijl f(a) = A en f(b) = B, dan heeft f een inverse functie f inv, die gedefinieerd is op [A, B] en monotoon stijgt (daalt). |
We zullen deze stelling in de volgende paragrafen volgt gebruiken.
2.
Cyclometrische functies
2.1. Sinus en arcsin
 |
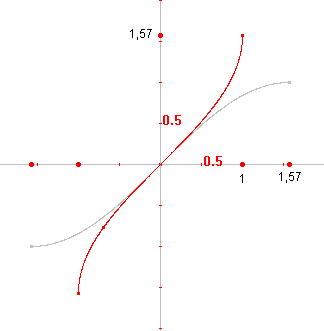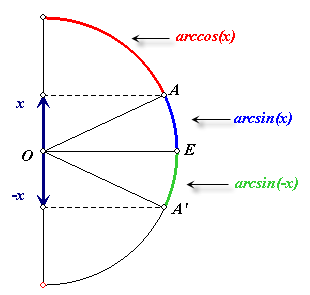
We bekijken allereerst de functie f(x) = sin x
op het interval [-½p. ½p]. Er geldt: f ´(x) = cos x, waarbij op het bedoelde domein geldt cos x ³ 0. De functiewaardenverzameling van f (het bereik) is [-1, 1]. f heeft dus een inverse functie g gedefinieerd op [-1, 1] met als bereik [-½p, ½p]. Deze inverse functie noemen we arcus sinus. We schrijven sininv = arcsin = bgsin. Spreek uit als: arcsinus resp. boogsinus. In de figuur hiernaast is de
grijze lijn de grafiek van f(x) = sin(x); de rode lijn is de
grafiek van De arcsin (of bgsin) behoort tot de familie van zogenoemde cyclometrische
functies. Zie ook de Opmerking na paragraaf 2.3 |
 |
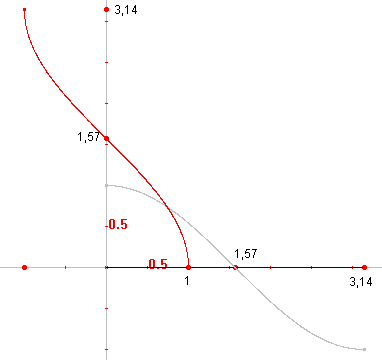De functie f(x) = cos x
bekijken we op het interval [0, p]. Voor de inverse van f op dit interval hebben we, eveneens vanwege de monotonie (maar nu dalend): g(x) = cosinv(x) = arccos(x) Inplaats van arccos schrijven we ook wel bgcos. Het domein van arccos is [-1,1]; het bereik is [0, p]. In de figuur hiernaast is de grijze lijn de grafiek van f(x) = cos(x); de rode lijn is de grafiek van g(x) = arccos(x). Zie ook de Opmerking na paragraaf 2.3 |
 |
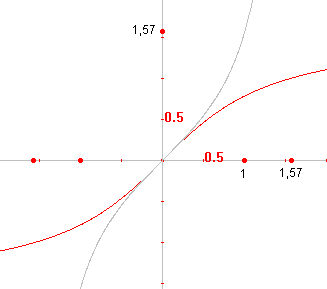De functie f(x) = tan x
bekijken we weer op het interval <-½p. ½p>. Voor de inverse van f op dit interval hebben we dan: g(x) = taninv(x) = arctan(x) In plaats van arctan schrijven we ook bgtan. Het domein van arctan is < - ¥, + ¥ >; het bereik is <-½p. ½p>. In de figuur hiernaast is de grijze lijn de grafiek van f(x) = tan(x);
de rode lijn is de grafiek van |
Opmerking
Op de in Nederland en Vlaanderen in gebruik zijnde (grafische) rekenmachines vinden we in
plaats van arcsin, arccos, arctan de
onjuiste notatie:
sin-1, cos-1, tan-1
[einde Opmerking]
3. Afgeleiden
Voor de volledigheid vermelden we ook de afgeleiden van de hierboven behandelde cyclometrische functies.
 |
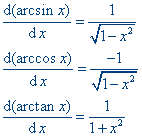
Zie voor het bewijs van deze afgeleiden het artikel "Over de functies arcsin, arccos en arctan"
(PDF-formaat, ca. 170 kB). In het artikel wordt ook de lengtemeting van een cirkel (met integraalrekening) behandeld. |
| Stelling Voor alle x in [-1 ; 1] geldt: arcsin(x) + arccos(x) = p/2 |
Bewijs:
 |
Klik hier > <voor
een 'aanschouwelijk bewijs' van deze stelling via een Cabrijavapplet.Uit
de figuur hiernaast blijkt dat voor x > 0: Voorts is verder onmiddelijk duidelijk, dat |
| . |
| Stelling arctan(1) + arctan(2) + arctan(3) = p |
Bewijs:
| Zie nevenstaande figuur, waarin: tan(A1) = 1, tan(A2) = 2, tan(A3) = 3. | .gif) |
[cyclomfunc.htm] laatste wijziging op: 15-02-06