Over de secans en de cosecans
Overzicht ][ Sinus, cosinus, tangens | Analyse
1. Definities ![]()
Op de pagina "Sinus, cosinus en tangens
als functies" zijn de sinus en de cosinus gedefinieerd als functie van een reŽle
variabele met behulp van de eenheidscirkel.
De omgekeerden van deze functies (niet te verwarren met de inverse
functies van sinus en cosinus) werden vroeger ook nog wel in het Nederlandse middelbaar
onderwijs behandeld. De omgekeerde functies komen mogelijk nog wel voor in het Vlaamse
onderwijs.
| Definities De functie secans wordt op de verzameling van de reŽle getallen gedefinieerd als: secans(x) = sec(x) = sc(x) = 1/cos(x) De functie cosecans wordt op de verzameling van de reŽle getallen gedefinieerd als: cosecans(x) = cosec(x) = csc(x) = 1/sin(x) |
Gevolg
Sec(x) is niet gedefinieerd voor x = Ĺp + k∑p (met k geheel).
Cosec(x) is niet gedefinieerd voor x = kp (met
k geheel),
immers voor die waarden van x is de noemer van de betreffende definiŽrende functie gelijk
aan 0.
[einde Gevolg]
2. Grafieken ![]()
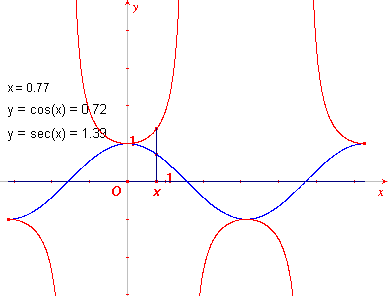
De grafieken kunnen door hun definitie direct uit de definiŽrende
functie worden afgeleid. Zie daarvoor onderstaande figuren waarin in rood
de grafieken van de functies zijn getekend op het interval [-Ĺp ;
2p]. De grafieken van de definiŽrende functies zijn blauw.
| f (x) = sec(x) | f (x) = cosec(x) |
 |
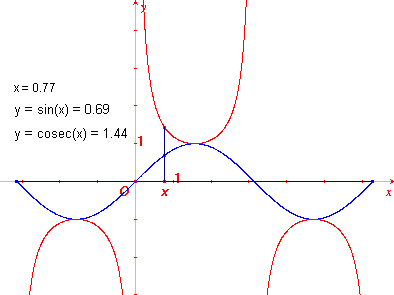 |
Duidelijk is dat beide functies een periode hebben van 2p.
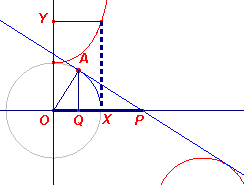
![]() Meetkundige eigenschap
- Beweegt het punt A over de eenheidscirkel, dan is de cosinus van de hoek tussen OA en de
positieve x-as gelijk aan de (van tekenvoorziene) afstand van A tot de y-as (zijnde de
x-coŲrdinaat van A). Zie definitie van de cosinus-functie op
de pagina "Sinus, cosinus, ...".
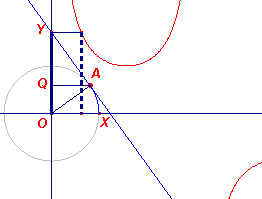
Meetkundige eigenschap
- Beweegt het punt A over de eenheidscirkel, dan is de cosinus van de hoek tussen OA en de
positieve x-as gelijk aan de (van tekenvoorziene) afstand van A tot de y-as (zijnde de
x-coŲrdinaat van A). Zie definitie van de cosinus-functie op
de pagina "Sinus, cosinus, ...".
We kunnen ook de waarde van de secans op de x-as
aflezen.
![]() Vreemde woorden - In
'Vreemde woorden in de wiskunde' (Dr. E.J. Dijkerhuis, P. Noordhoff, 1948) vinden we:
Vreemde woorden - In
'Vreemde woorden in de wiskunde' (Dr. E.J. Dijkerhuis, P. Noordhoff, 1948) vinden we:
Secans (sc. linea = snijdende lijn; Lat. part. praes. van secare = snijden). De goniometrische functie secans ontleent haar naam aan de wijze, waarop het lijnstuk secans in de figuur van den goniometrische cirkel [dk: de eenheidscirkel] voorkomt, nl. op een lijn door het middelpunt. Mv. secanten.
Cosecans. Afkorting voor complementi secans = secans van het complement. Mv. cosecanten.
3. Gebuik van de
functie h(x) = 1 / x ![]()
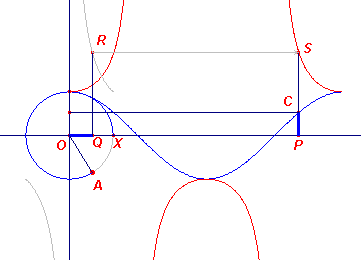 |
We kunnen beide functies ook opvatten als een samengestelde
functie. We laten dat hieronder alleen zien voor de functie f(x) = sec(x). Zij
h de functie gedefinieerd door h(x) = 1 / x. In de hiernaast staande figuur geldt: |
Klik hier >![]() <
voor een CabriJavapplet die dit illustreert.
<
voor een CabriJavapplet die dit illustreert.