Inversie en de Stelling van Feuerbach
Inleiding | Bewijs ][ Inversie | Cirkel van Feuerbach | Meetkunde
1. Inleiding ![]()
De stelling van Feuerbach (Karl Feuerbach, 1800-1834, Duitsland) luidt
| Stelling De negenpuntscirkel van een driehoek raakt aan de ingeschreven cirkel en aan de aangeschreven cirkels van die driehoek. |
Hierbij zijn de bedoelde negen punten:
- de middens van de zijden van de driehoek
- de voetpunten van de hoogtelijnen van de driehoek
- de middens van de lijnstukken die het hoogtepunt van de driehoek verbinden met de hoekpunten.
Deze stelling kan op elementaire wijze eveneens worden bewezen.
Klik hier voor een dergelijk bewijs (maar
dan alleen voor raking van de incirkel en de negenpuntscirkel).
Hieronder laten we het bewijs van de stelling volgen gebaseerd op de theorie der inversie.
Opmerking
De negenpuntscirkel wordt ook wel cirkel van Feuerbach of cirkel van
Euler genoemd.
[einde Opmerking]
2. Bewijs ![]()
We gaan uit van de incirkel en de aan zijde a (BC) aangeschreven cirkel (zie
figuur 1).
| figuur 1 |  |
I is het middelpunt van de incirkel; Ia is het het middelpunt
van de beschouwde aancirkel. Deze in- en aancirkel bepalen een in- en uitwendig gelijkvormigheidspunt, te weten het hoekpunt A en het snijpunt K van de centraal van de cirkels (de bissectrice van hoek A) met de zijde BC. Verder is de dubbelverhouding (A K I Ia) = -(IA/IK) : (IaA/IaK) = -(IA/IaA) : (IK/IaK) = -v : v = -1 Zijn X en Xa opvolgend de raakpunten en D de projectie van A op de (drager van de) zijde BC, dan is wegens het feit, dat de dubbelverhouding bij project invariant is, ook (D K X Xa) = -1 |
Er is dus sprake van hamonische ligging.
Zij nu A' het midden van de zijde BC (A' ligt dus op de negenpuntscirkel).
Omdat CXa = BX ( = s - c ), is A' dus ook het midden
XXa. Met andere woorden A'X = A'Xa.
Uit de eigenschap van het midden van een lijnstuk bij de
dubbelverhouding (D K X Xa), volgt
(A'X)2 = (A'Xa)2 = A'K
x A'D
Op basis van deze overweging kiezen we voor een inversie met centrum A' en
macht A'X ( = A'Xa).
Zie nu figuur 2.
| figuur 2 | 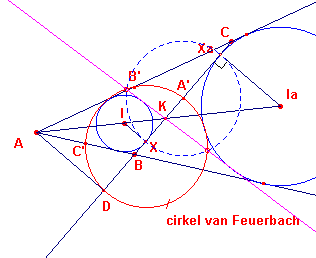 |
De cirkels I en Ia gaan door deze inversie over in zichzelf. Omdat de negenpuntscirkel door A' gaat, gaat deze over in een rechte lijn door het punt K. Immers K is de inverse D (zie bovenstaande dubbelverhouding) en D ligt als voetpunt van de hoogtelijn uit A ook op de negenpuntscirkel. Als we nu kunnen aantonen, dat deze lijn
(het beeld van de negenpuntscirkel) raakt aan de cirkels I en Ia zijn we klaar. |
| figuur 3 | 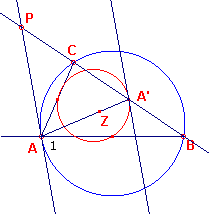 |
In figuur 3 zijn de raaklijn in A aan de omcirkel en de raaklijn in A'
aan de negenpuntscirkel getekend. Deze beide lijnen zijn evenwijdig omdat de negenpuntscirkel uit de omcirkel ontstaat door vermenigvuldiging met -½ met centrum Z. De raaklijn in A is antiparallel met BC (tov. hoek A), immers hoek C = hoek A1 (staan op dezelfde bg AB). De raaklijn in A' aan de negenpuntscirkel is dus eveneens antiparallel met BC. Omdat deze raaklijn bij de gebruikte inversie op zichzelf wordt afgebeeld, en dus evenwijdig is met het beeld van de negenpuntscirkel, is deze laatste ook antiparallel met BC. |
| Rest ons aan te tonen, dat de tweede door K gaande inwendige raaklijn van I en Ia ook antiparallel is met BC. |
| figuur 4 | 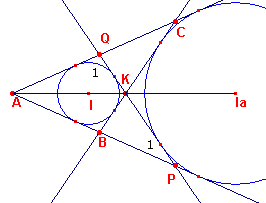 |
In figuur 4 zijn de gemeenschappelijke raaklijnen aan I en Ia
nogmaals getekend. Vanwege de symmetrie (in AIa) geldt: hoek P1 = hoek C Hieruit volgt dan, dat BC en PQ antiparallel zijn (tov. hoek A). De lijn PQ en de inverse van de negenpuntscirkel zijn dus evenwijdig en gaan beide door K (zie ook figuur 2). Hiermee is dus de stelling van Feuerbach bewezen. ¨ |
Opmerkingen
[1]
Een bewijs, anders dan het bovenstaande, staat in het artikel "De stelling van
Feuerbach, een bewijs met inversie" (PDF-bestand, ca. 13 Kb).
Klik hier
om dat bestand te downloaden.
[2]
De Stelling van Feuerbach kan ook met complexe getallen worden bewezen. Klik hier voor dat bewijs.
[einde Opmerking]
[feuerinv.htm] laatste wijziging op: 04-08-2008