Duale kegelsnede

Definitie cabrisignal | Toepassing | Download  ][  Proj.Meetkunde | Pooltransformaties | Cabri

Definitie terug

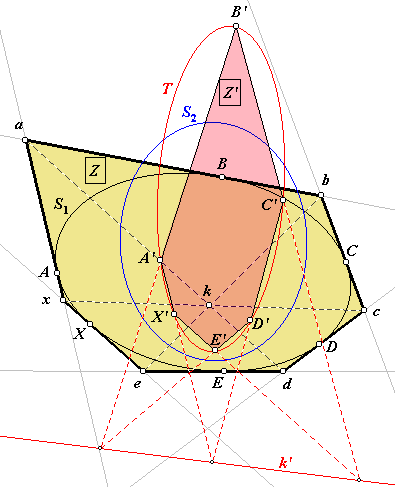duaalkeg1 We gaan uit van twee kegelsneden S1 en S2.

We kunnen de kegelsnede S1 opvatten als een lijn-kegelsnede, dwz. dat we S1 beschouwen als de omhullende van de raaklijnen.

Op S1 kiezen we de vaste punten A, B, ..., E. Op S1 ligt ook een variabel punt X.
S1 wordt dus bepaald door de vijf punten A, B, ..., E.
De zeshoek Z = abcdex wordt bepaald door de raaklijnen aan S1 in de punten A, ..., E, X.

Volgens de stelling van Brianchon (*) gaan van Z de verbindingslijnen van overstaande hoekpunten door hetzelfde punt k.

De punten A', B', ..., E', X' zijn de polen van de zes raaklijnen aan S1 ten opzichte van S2.

Van de zeshoek Z' = A'B'C'D'E'X' liggen nu de snijpunten van de overstaande zijden op dezelfde lijn k'; dit op basis van dualiteitsoverwegingen.

De punten A, ..., E zijn vaste punten. De punten A', ..., E' zijn dus eveneens vaste punten.
Wegens de omgekeerde stelling van Pascal (*) liggen de punten A', ..., E' op een kegelsnede T.

Als het punt X de kegelsnede S1 doorloopt, doorloopt het punt X' dus de kegelsnede T.

Afspraak: T heet de duale kegelsnede van S1 tov. S2.

(*) Opmerking
Zie de pagina "De stellingen van Pascal en Brianchon voor cirkels".
[einde Opmerking]

Klik hier >Animatie< voor een CabriJavapplet die het bovenstaande illustreert.

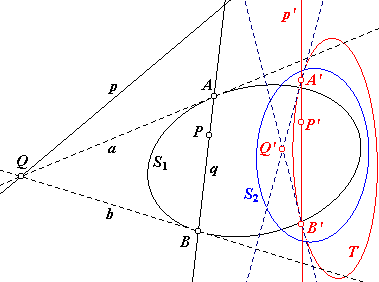duaalkeg2b In nevenstaande figuur is de dualiteit T van S1 tov. S2 nog eens algemeen weergegeven.
Hierbij is P een willekeurig punt en de lijn AB (= q) een willekeurige snijlijn van S1 waarop het punt P gelegen is.
De lijn p is de poollijn van P tov. S1.
De overige duale elementen zijn met accenten aangegeven.

Toepassing: gemeenschappelijke raaklijn aan twee kegelsneden terug

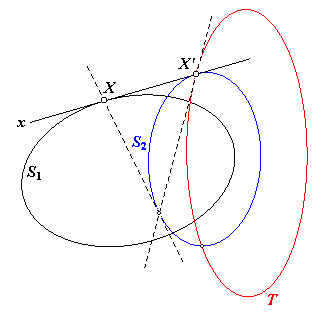duaalkeg2 In nevenstaande figuur zijn S1 en S2 willekeurige kegelsneden.
T is de duale kegelsnede van S1 tov. S2.
X en X' zijn 'toegevoegde' punten.
Het punt X ligt zo op S1, dat het punt X' samenvalt met één van de snijpunten van S2 en T.

De raaklijn x in het punt X aan S1 is nu poollijn van het punt X' tov. S2 (per definitie: X' is de pool van x tov. S2; zie de paragraaf Definitie).

Dus:
Omdat X' op S2 ligt, is die poollijn de raaklijn in X' aan S2.

We hebben hiermee een constructie gevonden voor de gemeenschappelijke raaklijnen aan twee kegelsneden.

Opmerking. De poollijn van X tov. S2 is (steeds) raaklijn aan T, vanwege de dualiteit tussen S1 en T.

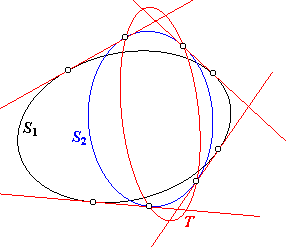duaalkeg3 Omdat twee kegelsneden (in casu S2 en T) elkaar in ten hoogste vier punten snijden, hebben twee kegelsneden dus ten hoogste vier gemeenschappelijke raaklijnen.

Download terug
Klik hier voor het downloaden van een bestand waarin Cabri-macro's zijn opgenomen voor de constructie van de duale kegelsnede van twee kegelsneden (DUALCONIC.ZIP; ca. 8 Kb). Het bestand bevat macro's voor Cabri Geometry II, vs. 1.0 (Windows) en vs. 1.2.5 (Windows).
In het bestand is ook opgenomen de figuur die gebruikt is voor bovenstaande CabriJavapplet.

up
[dualekegelsnede.htm] laatste wijziging op: 16-jul-05