Apollonius-hyperbool en normalen van een kegelsnede
Overzicht ][ ProjMeetkunde | AnalMeetkunde
Definitie (min of meer):
De Apollonius-hyperbool van een punt bij een kegelsnede is een
orthogonale hyperbool door dat punt en door het middelpunt van die kegelsnede.
 |
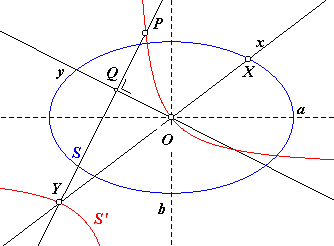In nevenstaande figuur is X een variabel punt op de
kegelsnede S. P is een vast punt. De lijnen x en y zijn toegevoegde middellijnen. Het snijpunt van de loodlijn uit P op y snijdt x in Y. De Apollonius-hyperbool is de meetkundige plaats S' van de punten Y. Klik hier
> |
We leiden het ontstaan van de Apollonius-hyperbool af en bespreken enkele eigenschappen
(oa. die welke samenhangen met normalen bij een kegelsnede).
Zie verder Download.
Definitie:
Een normaal in een punt van een kegelsnede is een lijn die loodrecht staat op de
raaklijn in dat punt aan een kegelsnede.
 |
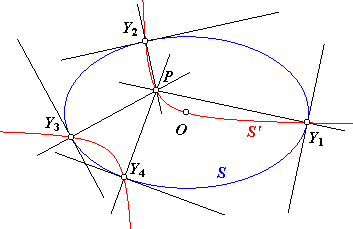In nevenstaande figuur is P een willekeurig vast punt. De punten Yi zijn de snijpunten van de kegelsnede S met de Apollonius-hyperbool S' van P bij S. Klik hier > |
We onderzoeken het aantal normalen dat gaat door een vast punt (niet
noodzakelijk een raakpunt) bij een kegelsnede.
Zie verder Download.
Download
Bovenbedoelde beschouwingen zijn opgenomen in een PDF-bestand (apolhyp.pdf, ca. 45 kB).
Klik hier om dat bestand te downloaden.
Nb. Een PDF-bestand kan met Adobe Reader® worden
gelezen 
De hierboven in de applets gebruikte Cabri-figuren kunnen in één
bestand worden gedownload.
Klik hier om het downloaden daarvan te
starten (ZIP-bestand, apolhyp(fig).zip; ca. 4 kB)
[p: apolhyp.htm] laatste wijziging op: 16-jul-05