Hyperbolische meetkunde [9]: Cabri-macro's

Pagina-overzicht ][ Complexe afbeeldingen | Andere Cabri-macro's | Meetkunde

Begin

0. Overzicht

Macro's
Beschrijving van de macro's
Download

1. Macro's

	Naam	Omschrijving

o	d-Lijn	Constructie van een lijn door twee d-punten
	Halve d-Lijn	Constructie van een halve d-lijn bepaald door het beginpunt en een d-punt (op de lijn)
o	d-Lijnstuk	Constructie van een lijnstuk door twee d-punten
o	d-Middellijn	Constructie van de middellijn van de disk bepaald door één d-punt
	d-Driehoek	Constructie van een driehoek bepaald door drie d-punten
	d-Vierhoek	Constructie van een vierhoek
o	d-Midden	Constructie van het midden van een lijnstuk
o	d-Loodlijn	Constructie van de loodlijn uit (in) een punt op een lijn
o	d-Middelloodlijn	Constructie van de middelloodlijn van een lijnstuk
o	bi-Parallel	Constructie van de twee lijnen door een punt parallel aan een lijn
o	bi-Loodlijn	Constructie van de gemeenschappelijke loodlijn van twee ultra-parallelle lijnen
o	SpiegelasCentrum	Constructie van de spiegelas die een punt op het centrum van de disk afbeeldt
o	Horocykel	Constructie van de horocykel van een oneigenlijk punt en een d-punt Een horocykel is een d-cirkel met middelpunt op de horizon door een 'echt' d-punt
o	Hypercykel	Constructie van de hypercykel van een d-punt bij een d-lijn Een hypercykel is de verzameling equidistante punten bij het gegeven d-punt en de gegeven d-lijn
o	d-Afstand overbrengen	Overbrengen van een afstand op een d-lijn in een punt
o	d-Cirkel	Constructie van een cirkel bepaald door het d-middelpunt en een d-punt op de omtrek
	d-Horizon	Constructie van de horizon, samen met coördinaatsassen (nodig voor Afstand-berekeningen)
o	d-Afstand	Berekening van de afstand van twee punten (assenstelsel nodig; zie macro:d-Horizon)
o	d-AfstandCentrum	Berekening van de afstand van een punt tot het centrum (assenstelsel nodig; zie macro:d-Horizon)

o	H₁(z)	Hyperbolische (standaard) afbeelding: H(z) = (z - m) / (1 - m_z)
o	H₁inv(z)	Inverse van de afbeelding H₁(z)
o	Middelpunt d-lijn	Constructie van het Euclidisch middelpunt van de drager van een d-lijn

2. Beschrijving van de macro's
In deze paragraaf staat een beschrijving van de belangrijkste macro's die vermeld zijn in paragraaf 1.
Van de meeste macro's is ook de (Euclidische) constructie opgenomen.

2.1. Macro: d-Lijn
Beschrijving
De macro tekent een d-lijn bepaald door twee d-punten.

figuur 1.1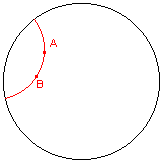

Helptekst:
"Constructie d-lijn
- Selecteer twee punten (evt. grenspunten) en de horizon"

Bijzonderheden
Indien de beide punten op een middellijn van de disk liggen, dan wordt geen d-lijn getekend.
In dit geval kan gebruik gemaakt worden van de gebruikelijke functies van Cabri of van de macro:d-middellijn.

Constructie

figuur 1.2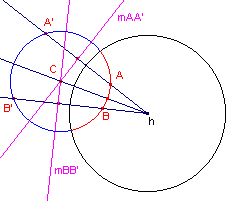

A' = Inversie(A, h)
B' = Inversie(B, h)
mAA' = Loodlijn op hA door midden van AA'
mBB' = Loodlijn op hB door midden van BB'
C = Snijpunt(mAA', mBB')
Cirkel(C, A)
P, Q (niet vermeld) = Snijpunten(Cirkel, h)
M (niet vermeld) = Snijpunt(hC, Cirkel)
Cirkelboog(P,M,Q)

2.2. Macro: d-Lijnstuk
Beschrijving
De macro tekent het lijnstuk bepaald door twee d-punten.

figuur 2.1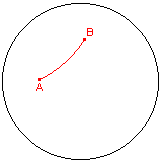

Helptekst:
"Constructie van een d-lijnstuk
- Selecteer twee punten (evt. grenspunten) en de horizon"

Bijzonderheden
Het middelpunt van de disk kan niet als eindpunt geselecteerd worden.
Gebruik hiervoor de gebruikelijke functie van Cabri.
Zie ook de macro:d-Middellijn.

2.3. Macro: d-Middellijn
Beschrijving
De macro tekent de middellijn van de disk bepaald door één d-punt.

figuur 3.1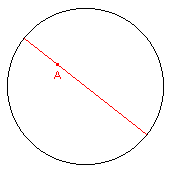

Helptekst:
"Constructie van een middellijn van de disk
- Selecteer een d-punt en de horizon"

Bijzonderheden
Een punt van de horizon kan niet gebruikt worden om een d-middellijn te tekenen.

2.4. Macro: d-Midden
Beschrijving
De macro tekent het d-midden van een d-lijnstuk.

figuur 4.1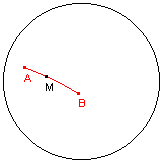

Helptekst:
"Constructie van het midden van een d-lijnstuk
- Selecteer het d-lijnstuk (of de eindpunten) en de horzion"

Bijzonderheden
Oneigenlijke punten kunnen niet als eindpunt worden geselecteerd.

Constructie

figuur 4.2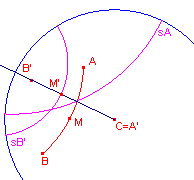

We beelden A (het ene eindpunt van het lijnstuk) af op C. We gebruiken hiervoor een spiegeling (de spiegelas is sA; zie macro:SpiegelasCentrum).
B' is dan het beeld van B. We moeten nu het d-midden van A'B" vinden. We construeren de spiegelas die B' op C (= A') afbeeldt (de d-lijn SB'). M' (het snijpunt van CB" en sB') is dan het d-midden van A'B'.
Spiegelen we M' nu weer in sA dan hebben we het punt M.

2.5. Macro: d-Loodlijn en macro: d-Middelloodlijn
Beschrijving
d-Loodlijn: De macro tekent de loodlijn uit (cq. in) een punt op een d-lijn.
d-Middelloodlijn: De macro tekent de d-lijn door het midden van een d-lijnstuk, loodrecht op dat d-lijnstuk.

figuur 5.1a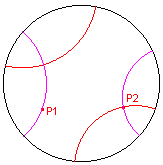

Helptekst:

d-Loodlijn:

"Constructie loodlijn in cq uit een punt op een d-lijn
- Selecteer het punt, de d-lijn en de horizon"

figuur 5.1b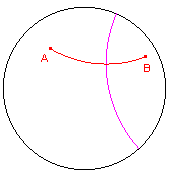

Helptekst:

d-Middelloodlijn:

"Middelloodlijn van een d-lijnstuk
- Selecteer het d-lijnstuk (of de eindpunten ervan) en de horizon"

Bijzonderheden
d-Loodlijn: Ook uit een oneigenlijk punt kan een loodlijn op een d-lijn worden getekend.
d-Middelloodlijn: De middelloodlijn is tevens de spiegelas van de spiegeling waarbij het punt A op het punt B (en omgekeerd) wordt afgebeeld (zie ook macro:SpiegelasCentrum).

Constructie d-Loodlijn

figuur 5.2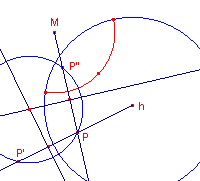

De drager van de gezochte d-lijn moet loodrecht staan op de gegeven d-lijn en door P gaan.
Het middelpunt van deze drager ligt dus op de middelloodlijn van P" (met P" is de inverse van P bij de inversie tov. de gegeven drager met middelpunt M).
De gezochte d-lijn staat ook loodrecht op de horizon, dus moet het middelpunt van de drager liggen op de middelloodlijn van PP' (P' is de inverse van P bij de inversie tov. de horizon).

Constructie d-Middelloodlijn
De middelloodlijn van een lijnstuk kan worden geconstrueerd met behulp van macro:d-Midden en macro:d-Loodlijn.

2.6. Macro: bi-Parallel
Beschrijving
De macro tekent de beide parallelle d-lijnen door een punt buiten een gegeven d-lijn.

figuur 6.1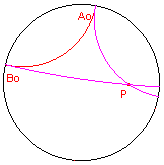

Helptekst:
"Constructie van twee lijnen door een d-punt evenwijdig aan een d-lijn
- Selecteer het d-punt, de d-lijn en de horizon"

Bijzonderheden
Geen.

Constructie

figuur 6.2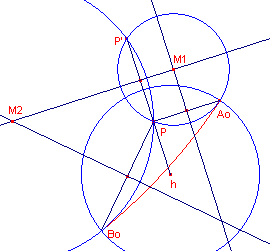

De gezochte d-lijnen staan loodrecht op de horizon. Ze gaan dus door het inverse punt van P' tov. de horizon.
De beide middelpunten. M₁ en M₂, liggen dus op de (Euclidische) middelloodlijn van PP'.
A_o en B_o zijn de oneigenlijke punten van de gegeven d-lijn. De middelpunten liggen dus ook op de (Euclidische) middelloodlijnen van PA_o en PB_o.

2.7. Macro: bi-Loodlijn
Beschrijving
De macro tekent de unieke d-lijn die loodrecht staat op twee ultra-parallelle d-lijnen.

figuur 7.1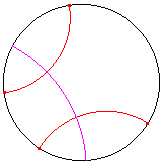

Helptekst:
"Constructie van de gemeenschappelijke loodlijn van twee (ultra-parallelle) d-lijnen
- Selecteer twee d-lijnen en de horizon"

Bijzonderheden
Geen.

Constructie

figuur 7.2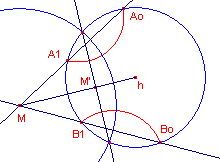

Het Euclidische middelpunt M van de gezochte cirkel ligt op de machtlijn van A_oA₁ en h en op de machtlijn van B_oB₁ en h.
M' is het inverse punt van tov. de horizon. De loodlijn in M' snijdt de horizon in de oneigenlijke punten van de gezochte d-lijn.

2.8. Macro: SpiegelasCentrum
Beschrijving
De macro tekent de spiegelas die een gegeven d-punt afbeeldt op het centrum van de disk.

figuur 8.1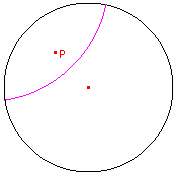

Helptekst:
"Spiegelas bij een spiegeling F waarbij F(P) = O
- Selecteer het d-punt P en de horizon"

Bijzonderheden
Spiegeling in een d-lijn wordt bewerkstelligd door inversie ten opzichte van de drager van die d-lijn.
In Cabri kan de inversie ook ten opzichte van een cirkelboog worden uitgevoerd.

Constructie

figuur 8.2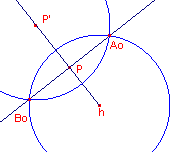

P' is het beeld van P bij inversie tov. de horizon.
De drager van de gezochte d-lijn is dus de boog van de cirkel met middelpunt P' die gaat door de snijpunten A_o en B_o van de loodlijn in P op hP' met de horizon.

2.9. Macro: Horocykel
Beschrijving
De macro tekent een d-cirkel met d-middelpunt op de horizon en door een gegeven d-punt (grenscirkel).

figuur 9.1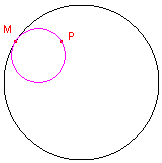

Helptekst:
"Constructie van een horocykel (grenscirkel)
- Selecteer een punt op de horizon (middelpunt), een d-punt (in deze volgorde) en de horizon"

Bijzonderheden
De volgorde van het selecteren van d-middelpunt en d-punt op de omtrek is duidelijk van belang!
Indien de selectievolgorde wordt omgekeerd, wordt de drager van de d-lijn getekend door het 'echte' d-punt die het punt op de horizon als oneigenlijk punt heeft.

Constructie

figuur 9.2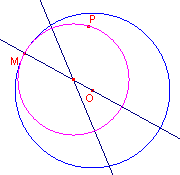

De horocykel is een Euclidische cirkel die de horizon in M (het d-middelpunt) raakt. Het Euclidische middelpunt ligt dus op de lijn OM.
De gezochte E-cirkel gaat door P; het E-middelpunt ligt dus ook op de E-middelloodlijn van het linstuk PM.

2.10. Macro: Hypercykel
Beschrijving
De macro tekent de hypercykel van een d-punt tov. en een d-lijn.
Een hypercykel is de verzameling van punten die dezelfde afstand tot de d-lijn hebben als het gegeven d-punt.

figuur 10.1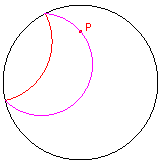

Helptekst:
"Constructie van een hypercykel
- Selecteer een d-lijn, een d-punt en de horizon"

Bijzonderheden
De hypercykel is geen d-lijn!

Constructie

figuur 10.2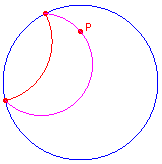

Op basis van de theorie kan de hypercykel worden geconstrueerd als Euclidische cirkelboog door de oneigenlijke punten van de d-lijn en het d-punt.

2.11. Macro: Afstand overbrengen
Beschrijving
De macro tekent twee d-punten op een lijn die een gegeven d-afstand (bepaald door een d-lijnstuk) hebben tot een gegeven d-punt op die d-lijn.

figuur 11.1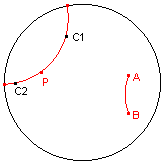

Helptekst:
"Overbrengen van een gegeven afstand op een d-lijn
- Selecteer een d-punt, de d-lijn waarop dit punt ligt, de afstand (als d-lijnstuk) en de horizon"

Bijzonderheden
Geen.

Constructie

figuur 11.2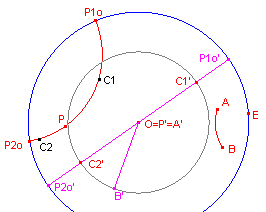

We beelden het punt P met de H-afbeelding F af op het punt O.
Hierdoor gaat de d-lijn zelf over in de d-middellijn P1_o'P2_o'.
Vervolgens beelden we A via een andere H-afbeelding G af op het punt O. Het punt B gaat hierbij over in B'.
Nu is OB' (d)= AB.
De verzameling van de punten die deze afstand tot O (= P') hebben is nu de Euclidische cirkel met middelpunt O en straal OB'.
Deze cirkel snijdt het beeld van de d-lijn in de punten C₁' en C₂'. Dit zijn de beelden van de gezochte punten C₁ en C₂.
Deze punten kunnen dus worden gevonden met de inverse afbeelding van de afbeelding F.

2.12. Macro: d-Cirkel
Beschrijving
De macro tekent de d-cirkel (een Euclidische cirkel) bij gegeven d-middelpunt en gegeven d-punt van de omtrek.

figuur 12.1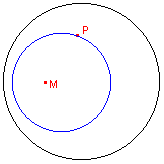

Helptekst:
"Constructie van een d-cirkel
- Selecteer het middelpunt, dan een punt van de omtrek en tenslotte de horizon"

Bijzonderheden
Geen.

Constructie

figuur 12.2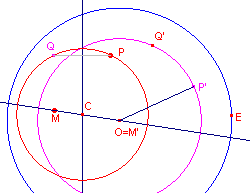

We kiezen weer een H-afbeelding F die het punt afbeeldt op het centrum O van de disk.
Hierdoor is OP', met P' = F(P), gelijk aan MP.
De verzameling van de punten P' is dus de cirkel (O, OP').
Het beeld van deze cirkel onder F^-1 is dan de gezochte cirkel.
We bepalen dit beeld door op de geconstrueerde cirkel een punt Q' te kiezen waarvan we Q = F^-1(Q') construeren.
Het snijpunt van de Euclidische middelloodlijn van PQ met de lijn OM is dan het middelpunt C van de gezochte cirkel.

2.13. Macro: d-Afstand en macro: d-AfstandCentrum
Beschrijving
d-Afstand: Deze macro berekent de afstand tussen twee d-punten, cq. de lengte van een d-lijnstuk.
d-AfstandCentrum: Deze macro berekent de afstand van een d-punt tot het centrum van de disk.

figuur 13.1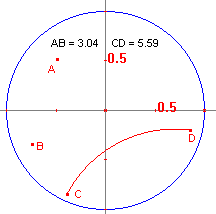

Helptekst:

d-Afstand:	"Berekening afstand tussen twee d-punten - Selecteer de punten (of het d-lijnstuk), de horizon en een d-as"
d-AfstandCentrum:	"Berekening van de afstand van een d-punt tot het d-centrum - Selecteer een d-punt en een d-as"

Een d-as is hier een as van het (Euclidische) assenstelsel dat op het Cabri-werkblad is vastgelegd. De horizon dient te gaan door het punt E(1,0).
Dit assenstelsel kan samen met de horizon via de macro:d-Horizon worden getekend.

Bijzonderheden
Omdat bij het berekenen van de afstand (cq. lengte) gebruik gemaakt wordt van coördinaten, is het noodzakelijk een zichtbaar assenstelsel te gebruiken. Dit stelsel moet samen met de horizon worden geselecteerd.
Na het uitvoeren van de macro moet de uitkomst door de gebruiker op het Cabri-werkblad worden geplaatst.
Zie ook Opmerking.

Constructie

figuur 13.2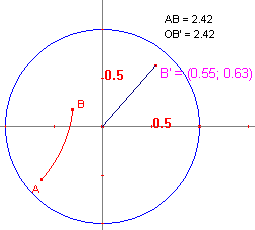

We beelden het punt A via een H-afbeelding af op het centrum O van de disk.
Hierdoor geldt AB (d)= OB'.
De lengte van AB kan dan met behulp van de coördinaten van het punt B' worden berekend.
Volgens de definitie is nu d(A, B) = 2artanh(a² + b²)^½.
In de illustratie hiernaast is a=0,56 en b=0,63, zodat
d(A,B) = 2artanh(0,8363) = 2 x 2,21 = 2,42.
Cabri berekent deze waarde eveneens, en maakt daarbij gebruik van dezelfde formule (zie echter Opmerking).

Opmerking
In het Engelstalige handboek bij Cabri (Getting Started with Cabri Geometry II, pg 11-9) ) staan, wiskundig gezien niet geheel juist, de volgende syntax-mogelijkheden om artanh als functie te gebruiken in Cabri's "Rekenmachine":
Arc Hyperbolic Tangent: ARCTH(value), arcth(value), ArcTh(value).
De juiste omschrijving van de functie is echter "area hyperbolic tangent" (Ned. area tangens hyperbolicus of area hyperbolische tangens).
Ook kunnen ARTH(value) en ARCTANH(value) worden gebruikt.
[einde Opmerking]

2.14. Macro: H₁(z) en macro: H₁inv(z)
Beschrijving
H₁(z): De macro tekent het beeld van een d-punt (z) bij de H-afbeelding die een gegeven d-punt (m) afbeeldt op het centrum O van de disk.
H₁inv(z): De macro tekent het beeld van een d-punt (z') bij de inverse van de H-afbeelding H₁(z).

figuur 14.1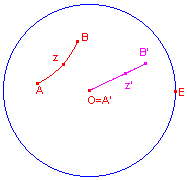

Helptekst:

H₁(z):	"Constructie H1(z)=(z-m)/(1-m_z) - Selecteer z, m, O en E (in deze volgorde)"
H₁inv(z):	"Constructie H1inv(z)=(z+m)/(1+m_z) - Selecteer z, m, O en E (in deze volgorde)"

In de figuur hiernaast is de afbeelding H₁(z) geïllustreerd.
Het punt A is afgebeeld op O; het punt z (Punt op object) is afgebeeld op z'.
Het beeld van het d-lijnstuk AB is bepaald met de functie "Meetkundige plaats".

Bijzonderheden
Voor de constructie (zie Helptekst) is een punt op de horizon nodig, dat fungeert als het punt E (z = 1).

2.15. Macro: Middelpunt d-lijn
Beschrijving
De macro tekent het Euclidisch middelpunt van de drager van een gegeven d-lijn.

figuur 15.1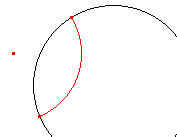

Helptekst:
"Constructie middelpunt van de drager van een d-lijn
- Selecteer de d-lijn"

Bijzonderheden
Deze macro kan van pas komen bij constructies in de P-meetkunde waarbij het middelpunt van de Euclidische boog (de d-lijn) nodig is.
Dit Euclidisch middelpunt ligt dus steeds buiten de disk en is dus geen d-punt!

3. Download
Alle bovengenoemde macro's zijn in één bestand te downloaden via deze website.
De macro's die in het bestand zijn opgenomen, zijn voor het merendeel nog onderhevig aan kleine wijzigingen, vandaar dat het bestand van een versienummer is voorzien. In het bestand lees_dit.txt wordt aangegeven welke macro's gewijzigd zijn ten opzichte van de vorige versie(s).
Vanaf versie 3.0 zijn in het bestand ook enkele macro's opgenomen die hierboven niet behandeld (of genoemd) zijn.
Klik hier om het downloaden te starten [ZIP-formaat, versie 3.1, ca. 24Kb].

Op de meeste pagina's over het Poincaré-model zijn animaties met CabriJava opgenomen.
De daarvoor gebruikte Cabri-figuren zijn eveneens te downloaden via deze website.
Klik hier om het downloaden van de figuren te starten [ZIP-formaat, ca. 48Kb].

Begin

[hypm9.htm] laatste wijziging op: 03-06-2000