Hyperbolische meetkunde [10]: een halfvlak-model

Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde

Begin

Overzicht

Een functie die de disk afbeeldt op een halfvlak
     1.1. De functie en het beeld van de disk
     1.2. d-Middellijnen
     1.3. d-Lijnen
Enkele eigenschappen

1. Een functie die de disk afbeeldt op een halfvlak
1.1. De functie en het beeld van de disk
Het is via een Möbius transformatie mogelijk de disk van het Poincaré-model van de hyperbolische meetkunde af te beelden op een deel van het complexe vlak.
In dit geval bekijken we de afbeelding van de disk op het deel van het vlak met Im(z) > 0.

We gebruiken daartoe de Möbius-transformatie:

Hieruit zien we onmiddellijk
   G(0) = i
   G(1) = ¥
   G(-1) = 0
   G(i) = (i - 1) / (1 - i) = -1
Voor reële a hebben we nu G(a) = i (1+a) / (1-a).
De reële as van de disk (met |a| < 1) wordt dus afgebeeld op het positieve deel van de imaginaire as.

Voor punten z = a+bi op de horizon geldt: a² + b² = 1.
Nu is:
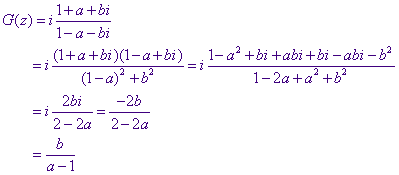
hypm012
De waarde van G(z) is dus in dit geval reëel. De horizon wordt dus afgebeeld op de reële as.

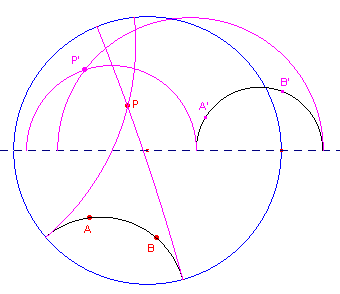
figuur 1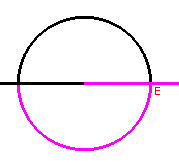

We hebben
   G(1) = ¥
   G(i) = i(1 + i) / (1 - i) = (i - 1)/(1 - i) = -1
   G(-1) = 0
De "bovenhorizon" wordt dus afgebeeld <-¥, 0]; de "onderhorizon" op [0,¥ >.
Uit de oriëntatie op de cirkel (tegenwijzerichting) volgt dat de disk wordt afgebeeld op het bovenhalfvlak.
De oneigenlijke punten van d-lijnen hebben dus punten op de reële as als beeld.
De reële as is dus in dit model de horizon.

1.2. d-Middellijnen
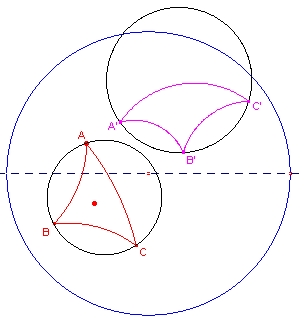
We hebben reeds gezien dat G(0) = i.

figuur 2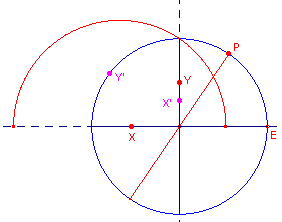

Middellijnen van de disk worden dus afgebeeld op halve cirkels door z = i, waarvan het middelpunt op de x-as ligt, met uitzondering van de "reële" middellijn.
Deze wordt afgebeeld op de halve rechte door O loodrecht op de x-as.
Voor de "imaginaire" middellijn hebben we
G(i) = -1
G(0) = i
G(-i) = i(1 - i)/(1 + i) = (i + 1)/(1 + i) = 1
Het beeld is dan de "bovenhorizon".

Klik hier voor een animatie van figuur 2.

1.3. d-Lijnen

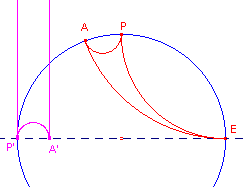
figuur 3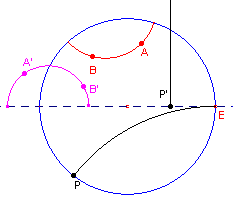

d-Lijnen uit het disk-model van Poincaré worden in het algemeen afgebeeld op halve cirkels waarvan het middelpunt op de x-as ligt., echter met uitzondering van de d-lijnen die E als oneigenlijk punt hebben. Deze laatste d-lijnen worden afgebeeld op halve lijnen loodrecht op de x-as.

Klik hier voor een animatie van figuur 3.

2. Enkele eigenschappen
De hyperbolische meetkunde in het bovenhalfvlak heeft veel eigenschappen die overeenkomen met die in het disk-model:

de som van de hoeken van een driehoek is kleiner dan 180°;
twee driehoeken zijn congruent als hun (overeenkomstige) hoeken gelijk zijn;
de oppervlakte van een driehoek is gelijk aan p - (A + B + C);
cirkels in het bovenhalfvlak zijn Euclidische cirkels.

Voorbeelden

figuur 4		[1] Hiernaast is AB een willekeurige d-lijn en P een willkeurig d-punt. Door P zijn de beide lijnen getekend die parallel zijn aan AB. De beelden van deze figuren onder de afbeelding G hebben dezelfde eigenschappen. Klik hier voor een animatie van figuur 4.
figuur 5		[2] Driehoek ABC is een regelmatige d-driehoek. Ook is de omgeschreven cirkel van ABC getekend. Deze cirkel is Euclidisch. De omgeschreven cirkel van driehoek A'B'C' is eveneens een Euclidische cirkel. Klik hier voor een animatie van figuur 5.
figuur 6		In figuur 6 is: E: z = 1 P: z = i Het punt A ligt op de horizon. Verder is E' = G(E) = ¥ Driehoek AEP wordt dus afgebeeld op een "oneindige" strook. Klik hier voor een animatie van figuur 6.

[einde Voorbeelden]

Begin

[hypm01.htm] laatste wijziging op: 03-06-2000