Hyperbolische meetkunde [5]: Cirkels, ed.

Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde

Begin

0. Overzicht

Cirkels in de H-meetkunde
Grenscirkel (horocykel of grenscirkel)
Equidistante krommen bij een d-lijn (hypercykel)
2.1. Inleiding
2.2. Onderzoek

1. Cirkels in de H-meetkunde
We definiëren een cirkel op de gebruikelijke manier:

Definitie
Een d-cirkel met straal r en centrum A is de verzameling punten X, waarbij de d-afstand d(A,X) = r.

Het blijkt dat een d-cirkel een Euclidische cirkel is. Echter het middelpunt van de d-cirkel valt in het algemeen niet samen met het Euclidische middelpunt. We zullen dat zien in de volgende stelling.

Stelling 1
Een d-cirkel met middelpunt A is een Euclidische cirkel die loodrecht staat op alle d-lijnen die door het d-punt A gaan.

Bewijs:
Alle d-lijnen die door A gaan, gaan ook door het punt A', dat het inverse punt is van A bij inversie tov. de horizon (zie figuur 1).

figuur 1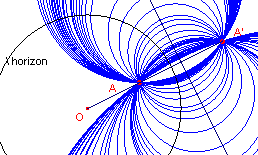

figuur 2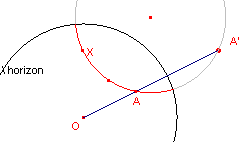

Zij nu X een d-punt van de omtrek van de d-cirkel met d(A,X) = r. Zij verder m de d-lijn door de punten A en X. De drager van m gaat nu door A' (zie figuur 2).
De lijn m is dus een exemplaar uit de coaxiale bundel cirkels (cirkels met de machtlijn AA') met as AA'.
We kiezen nu een inversiecirkel met middelpunt A' die loodrecht staat op de horizon (zie figuur 3).

figuur 3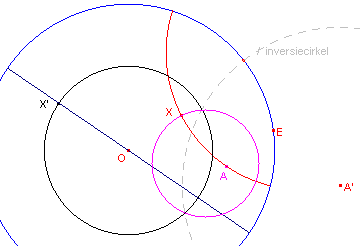

Onder deze inversie wordt de horizon (niet-puntsgewijs) op zichzelf afgebeeld. De d-lijn AX wordt dan afgebeeld op een middellijn van de disk, omdat de drager van AX door het punt A' gaat. En dit geldt dus voor alle d-lijnen door A.
Het beeld van A is dan het punt O.
Onder de H-afbeelding F, waarbij A op O wordt afgebeeld, wordt X op X' afgebeeld.
Omdat d-afstanden onder F invariant zijn, is nu d(O,X') = d(A,X) = r.
De verzameling van de punten X' (als beeld van de punten X waarvoor d(A, X) = r) is dus de Euclidische cirkel C ' met middelpunt O en straal OX'.
C ' staat loodrecht op alle middellijnen die door O gaan. Het origineel van C ' onder de inversie staat dan dus loodrecht op alle d-lijnen die door A gaan en is dus een Euclidische cirkel. ¨

Gevolg
Als het d-punt A op de horizon ligt, dan raakt de d-cirkel met middelpunt A en straal r in A aan de horizon.
De cirkel heet dan horocykel (Eng. horocycle), of ook wel grenscirkel (zie figuur 4a).

figuur 4a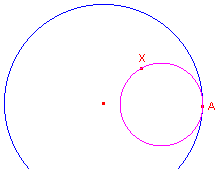

Klik hier

voor een animatie.
Deze animatie illustreert het verband tussen een cirkel door een punt en de horocykel van dat punt.

[einde Gevolg]
Opmerking
In het geval dat A' (A' is het beeld van A bij de inversie tov. de horizon) een eindig punt is, valt het Euclidische middelpunt van de cirkel NIET samen met het punt A.
We kunnen dit als volgt nagaan.
De d-cirkel behoort tot de bundel B₂ van Euclidische cirkels die orthogonaal zijn met de bundel B₁ van Euclidische cirkels door de punten A en A' (de horizon behoort tot de bundel B₂). Zie figuur 1 voor de bundel B₁.
De beperking die we aan deze d-cirkel opleggen, is dat hij geheel gelegen is op de disk (dus binnen de horizon, immers alle punten van de cirkel moeten d-punten zijn).
Het (Euclidische) middelpunt M van de d-cirkel moet nu liggen op de lijn AA'.
Er zijn nu vier mogelijkheden voor de positie van het punt M (zie figuur 4b):

figuur 4b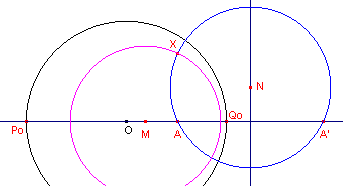

(i) ligt M links van O, dan ligt de d-cirkel buiten de disk (als M = O, dan valt de d-cirkel samen met de horizon);
(ii) ligt M tussen O en A dan is voldaan aan de voorwaarde: de d-cirkel ligt op de disk;
(iii) ligt M tussen A en Q_o, dan bestaat de d-cirkel niet;
(iv) ligt M rechts van Q_o, dan bestaat de d-cirkel niet, of de d-cirkel ligt buiten de disk.
Valt M met A samen dan is sprake van een punt cirkel (de straal van de d-cirkel is gelijk aan 0).
[einde Opmerking]

Stelling 2
Twee grenscirkels beide rakend aan de horizon in punt P_o snijden van alle d-lijnen die Po als oneigenlijk punt hebben, gelijke lijnstukken af.

Klik hier voor een animatie van Stelling 2.

Bewijs:
Zijn m en n de bedoelde grenscirkels, en zijn A₁B₁ en A₂B₂ d-lijnen met P_o als oneigenlijk punt, waarbij A_i en B_i de snijpunten zijn met die grenslijnen (zie figuur 5a).
We kiezen nu een inversie van de figuur tov. een cirkel met middelpunt P_o.
De dragers van beide d-lijnen gaan daardoor over in rechte lijnen.
De beelden h', m', n' van h (de horizon), m, n zijn dan evenwijdig.
De beelden van de beide d-lijnen staan loodrecht op die evenwijdige lijnen (zie figuur 5b).
Het beeld van Po is het punt ¥ van het uitgebreide Euclidische vlak.
Nu is A₁'Q₁' = A₂'Q₂' en ook B₁'Q₁'=B₂'Q₂' (Euclidisch gezien).
De dubbelverhouding (A₁,B₁;Q₁,P_o) is gelijk aan (A₁',B₁';Q₁',¥ ) = Q₁'A₁'/Q₁'B₁', omdat de inversie de dubbelverhoudig invariant laat. Dit geldt ook voor de dubbelverhouding (A₂,B₂;Q₂,P_o).
De d-afstanden A₁B₁ en A₂B₂ zijn dus gelijk. ¨

figuur 5a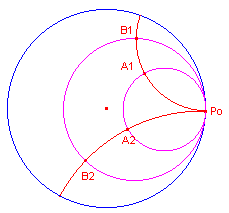

figuur 5b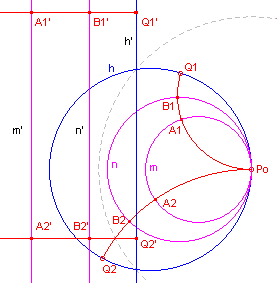

Klik hier voor een animatie van Figuur 5b.

2. Equidistante krommen bij een d-lijn (hypercykel)
2.1. Inleiding
In de Euclidische meetkunde wordt de verzameling punten die een gegeven afstand r hebben tot een rechte lijn, gevormd door twee evenwijdige lijnen die evenwijdig zijn met die lijn (op afstand r).
Ook nu is de situatie in de H-meetkunde duidelijk anders.

Allereerst:

Definitie
De d-afstand van een d-punt X tot een d-lijn m is de d-lengte van het lijnstuk met eindpunten X en het voetpunt A van de d-loodlijn op de d-lijn m.
Notatie: d(X, m) = d(X, A).

figuur 6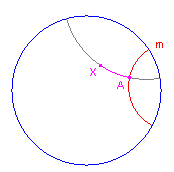

We gaan uit van een vast punt R waarvoor de afstand tot de lijn m dus bepaald is.
Zij nu d(R, m) = r.
Voor de verzameling van de equidistante (op gelijke afstand liggende) punten X moet nu (in de H-meetkunde) worden voldaan aan:
voor elk punt X van die verzameling moet gelden d(X, m) = r.

De d-dlijn m kan worden afgebeeld op een middellijn van de disk (door een willekeurig d-punt van m af te beelden op het centrum van de disk.
We kunnen dus voor het onderzoek naar de equidistante punten uitgaan van een middellijn van de disk

2.2. Onderzoek
We gaan uit van twee d-loodlijnen RA en SB op de middellijn. Zie figuur 7 voor de naamgeving van de verschillende punten.

figuur 7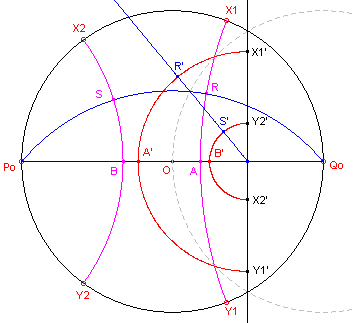

We kiezen een inversie ten opzichte van de cirkel door O met middelpunt Qo.
Hierdoor gaan de beide d-loodlijnen over in (delen van) concentrische cirkels met middelpunt Po' (het beeld van Po onder de inversie).
AB wordt dan afgebeeld op zichzelf.
Het beeld van de horizon is een lijn door Po' loodrecht op de lijn AB
De beelden R' en S' van R en S liggen op de concentrische cirkels.
Zoals bekend is de dubbelverhouding tussen vier punten invariant onder een inversie, dus
(A,R;X₁,Y₁) = (A',R';X₁',Y₁') en
(B,S;X₂,Y₂) = (B',S';X₂',Y₂')
Indien nu de d-afstanden d(A,R) en d(B,S) aan elkaar gelijk zijn, moeten de punten R' en S' op een rechte lijn liggen door het punt Qo'.
De gezochte verzameling is dus het inverse beeld van deze lijn ten opzichte van de gebruikte inversie, dat is een Euclidische cirkel.

De equidistante kromme (bepaald door R) is dus een deel van een (Euclidische) cirkel door R en door de oneigenlijke punten P_o en Q_o van de lijn AB.
We hebben dus bewezen:

Stelling 3
De equidistante kromme van het punt R ten opzichte van een d-lijn m is de (Euclidische) cirkelboog door R en de oneigenlijke punten van de lijn m.

Klik hier voor een animatie van stelling 3.

Opmerkingen

figuur 8a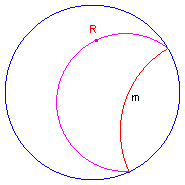

figuur 8b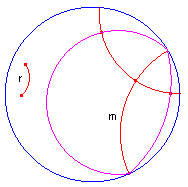

[1]
Deze equidistante kromme wordt ook wel de hypercykel (Eng. hypercycle) van R en m genoemd.
[2]
Vanwege de symmetrie bestaat de verzameling van punten die een gegeven afstand r hebben tot een d-lijn m dus uit twee hypercykels (zie figuur 8b)

[einde Opmerkingen]

We kunnen de afstand tussen een hypercykel en de bijbehorende lijn (de as van de hypercykel) ook uitdrukken in de hoek tussen de hypercykel en de lijn.
Zij a die bedoelde hoek (zie figuur 9a).

figuur 9a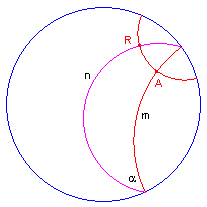

figuur 9b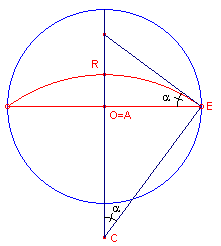

Dan is

Stelling 4
Gegeven is de d-lijn m, en is n de hypercykel die met m een hoek maak van a, dan is de d-afstand van de punten van n tot m gelijk aan
2arth(tan(½a)).

Klik hier voor een animatie van Stelling 4.

Bewijs: Zie figuur 9b.
We kunnen de lijn m afbeelden op een middellijn van de disk. Door een rotatie kunnen we dan een oneigenlijk punt van m' laten samenvallen met E (1,0). Daarna is het mogelijk het punt A af te beelden op het centrum van de disk. We krijgen dan figuur 9b.
Hierin is (Euclidisch) hoek OCE = a.
De d-afstand d(R,A) van figuur 9a is in figuur 9b gelijk aan de d-lengte van het lijnstuk RA.
Zij nu R: z = q i
en is r de (Euclidische) straal van de hypercykel.
Dan is (volgens de Euclidische goniometrie)
OE / CE = 1 / r = sin a, of r = 1 / sin a
zodat
   q = r - r cos a = (1 - cos a) / sin a
Toepassing van cos2x = 1-sin²x en sin2x = 2sin x cos x geeft dan (na overgang op halve hoeken):
   q = 2sin2(½a) / 2sin(½a)cos(½a)
      = tan(½a)
Voor de d-afstand d(R,A) hebben we dan
   d(R,A) = 2arth(tan(½a))
of ook, omgezet in logaritmen,
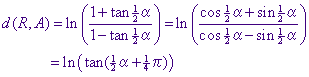    hypm5f1 ¨

Begin

[hypm5.htm] laatste wijziging op: 03-06-2000