Hyperbolische meetkunde [2]: Parallellen
Pagina-overzicht ][ Complexe afbeeldingen | Meetkunde
- Parallellen
Hulpstelling (E-meetkunde)
Stelling 1 (P-meetkunde)
Stelling 2 (P-meetkunde) - Euclides' 5e postulaat
- De hoekensom van een d-driehoek
Stelling 3 (E-meetkunde)
Stelling 4 (P-meetkunde)
Stelling 5 (P-meetkunde)
Stelling 6 (P-meetkunde)
1. Parallellen
We bewijzen allereerst een hulpstelling (uit de Euclidische meetkunde) waarvan de
toepassing in de P-meetkunde tot verrassende gevolgen aanleiding geeft (en heeft gegeven).
In de Euclidische bewijzen gebruiken we evenwel, daar waar dit verduidelijking geeft, ook
termen uit de P-meetkunde, zoals "horizon" en "oneigenlijk punt".
| Hulpstelling (Euclidisch) Als twee elkaar rakende cirkels orthogonaal zijn met een derde cirkel, dan ligt het raakpunt van die cirkels OP de derde cirkel. |
Bewijs:
We bewijzen uit het ongerijmde (zie figuur 1a).
| figuur 1a | 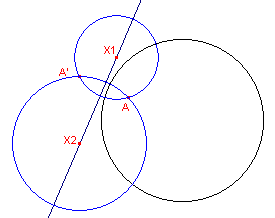 |
figuur 1b | 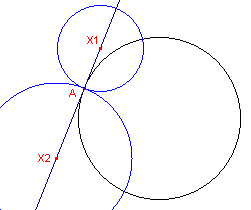 |
Stel het raakpunt A ligt NIET op de derde cirkel. Het inverse punt A' van A (tov. die
derde cirkel, de horizon van de P-meetkunde) ligt dan op beide orthogonaal
cirkels. Deze cirkels hebben dus twee verschillende punten gemeenschappelijk en
raken elkaar dus niet.
Dit is in strijd met het gegeven.
Met andere woorden: het raakpunt A ligt op de derde cirkel.¨
| Gevolg 1 (Euclidisch) Door een punt P buiten een cirkel die orthogonaal is met een andere cirkel (met oneigenlijke punten A en B op de horizon) gaan in het algemeen twee orthogonaal cirkels die aan de gegeven cirkel raken. |
Bewijs:
| figuur 2 | 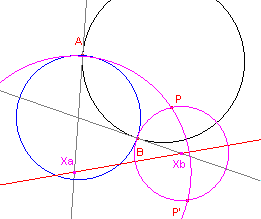 |
(zie figuur 2) Allereerst raking in A. Het middelpunt Xa van de gezochte raakcirkel ligt op de raaklijn in A aan de horizon, en ook op de middelloodllijn van PP' (waarbij P' inversie-beeld is van bij in de horizon; dit vanwege het loodrecht snijden). Er is dus één cirkel door P die in A raakt. Evenzo is er slechts één cirkel door P die in B raakt. Dus: door het punt P gaan twee cirkels ¨ Opmerking |
| figuur 3 | 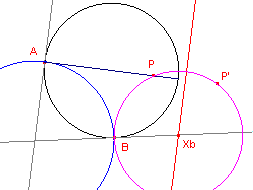 |
De middelloodlijn van PP' is nu evenwijdig met de raaklijn in
A aan de horizon. Er is dan geen raakcirkel in het punt A. De middelllijn door A (waarop
P ligt) snijdt de horizon echter wel loodrecht. |
| Gevolg 2 (E-meetkunde) Er zijn oneidig veel cirkels door zo'n punt P en orthogonaal met de horizon, die een andere orthogonaal cirkel niet snijden. |
| figuur 4 |  |
Op basis van bovenstaande resultaten kunnen we nu definities geven mbt. evenwijdigheid
van d-lijnen (in de P-meetkunde).
We introduceren hierbij de termen "parallel" en "ultra-parallel".
| Definities (P-meetkunde) Twee d-lijnen zijn parallel als ze elkaar snijden in een oneigenlijk punt. Twee d-lijnen zijn ultra-parallel als ze elkaar niet snijden. Twee d-lijnen zijn evenwijdig als ze parallel of ultra-parallel zijn. |
| Stelling 1 (P-meetkunde) Door een d-punt buiten een gegeven d-lijn gaan precies twee d-lijnen die parallel zijn met die gegeven d-lijn. |
| figuur 5 | 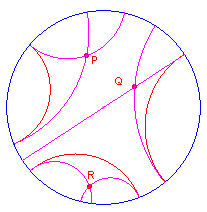 |
Bewijs: Zie Gevolg 1 van de hulpstelling en de Opmerking daarbij. ¨ In figuur 5 zijn enkele d-parallelen getekend. |
Een gevolg van deze definitie is
| Stelling 2 (P-meetkunde) Twee d-lijnen snijden elkaar in ten hoogste één punt. |
Bewijs: (zie figuur 5)
De dragers van twee verschillende d-lijnen (twee cirkels die beide orthogonaal zijn met de
horzon) snijden elkaar in 2, 1 of 0 punten.
Snijden de dragers elkaar in 1 of 0 punten, dan zijn de d-lijnen evenwijdig. De d-lijnen
hebben dan geen punt gemeenschappelijk.
Snijden de dragers elkaar in 2 punten, dan behoort slechts één van die punten tot de
disk D. Deze snijpunten zijn immers elkaar
beeld bij inversie tov. de horizon). De d-lijnen hebben dan 1 punt gemeenschappelijk. ¨
2. Euclides' 5e postulaat
In paragraaf 1 is in stelling 1 een eigenschap van de P-meetkunde bewezen.die ten nauwste
samenhangt met het 5e postulaat van Euclides (zie ook de pagina "Elementen").
We geven hieronder deze samenhang kort weer.
Het 5e postulaat luidt:
En [laat geëist zijn] dat, als een rechte, die twee rechten treft, de binnenhoeken aan dezelfde kant kleiner dan twee rechte [hoeken] maakt, de twee rechten, tot in het oneindige verlengd, elkaar ontmoeten aan de kant, waar de hoeken kleiner zijn dan twee rechte [hoeken]
John Playfair
(1748-1819, Schotland) heeft aangetoond, dat Euclides' 5e postulaat equivalent is met:Door een punt buiten een rechte gaat precies één rechte lijn die met die rechte parallel is
Voor een bewijs van deze equivalentie zie de uiteenzetting over Propositie I, 27 (Elementen) op deze website.
De P-meetkunde is blijkbaar een meetkunde waarin Playfair's axioma niet geldt.
Dat we de eigenschap van twee parallele lijnen door een punt buiten een lijn in de
P-meetkunde als stelling kunnen bewijzen, is gelegen in het feit, dat we de
P-meetkunde binnen de Euclidische meetkunde hebben gedefinieerd.
Willen we de P-meetkunde afzonderlijk opbouwen, dan dienen we het 5e postulaat van Euclides te vervangen door
Door een punt buiten een rechte gaan ten minste twee rechte lijnen die met die rechte parallel zijn
3. De hoekensom van een d-driehoek
We kijken nu eerst naar de hoekensom in de Euclidische meetkunde. Bij het bewijs in de
E-meetkunde wordt gebruik gemaakt van het axioma van Playfair (dus van
het 5e postulaat van Euclides).
| Stelling 3 (E-meetkunde) De som van de hoeken van een driehoek is gelijk aan twee rechte hoeken (is dus 180°). |
| figuur 6 | 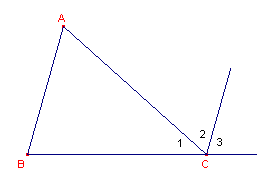 |
Bewijs: Trek door het hoekpunt C van driehoek ABC de lijn die evenwijdig is met de zijde AB (5e axioma). Dan is Ð C2 = Ð A en Ð C3 = Ð B (eigenschappen bij evenwijdige lijnen in de E-meetkunde: F- en Z-hoeken). Nu is Ð A + Ð B + Ð C = Ð C2 + Ð C3 + Ð C1 = 180°.¨ |
Gevolg
Aangezien in de P-meetkunde het in stelling 3 gebruikte axioma niet
geldt, is dus duidelijk, dat de hoekensom van een d-driehoek in de P-meetkunde niet
gelijk is aan 180°.
Voordat we deze hoekensom bekijken, geven we eerst de volgende (noodzakelijke) definitie:
| Definitie (P-meetkunde) De hoek tussen twee snijdende d-lijnen (of d-lijnstukken) is de hoek tussen de raaklijnen in het snijpunt aan de dragers van die d-lijnen (d-lijnstukken). |
Opmerkingen
[1]
H-transformaties zijn conform. Bovenstaande definitie is dus "toegestaan" in de
P-meetkunde.
[2]
De hoek tussen twee parallelle d-lijnen is hiermee niet gedefinieerd.
Indien we deze toch willen vastleggen, dan is de volgende definitie op zijn plaats:
| Definitie (P-meetkunde) De hoek tussen twee evenwijdige d-lijnen is 0°. |
Kijken we naar twee parallele d-lijnen, dan is de hoek tussen de dragers gelijk aan 0°. De definitie is dus conform hetgeen we in de E-meetkunde kunnen vaststellen: de hoek tussen twee raken cirkels is 0° (zie figuur 6b).
| figuur 6b | 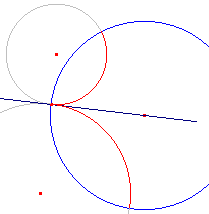 |
[einde Opmerkingen]
| Stelling 4 (P-meetkunde) De som van de hoeken van een d-driehoek is kleiner dan 180°. |
Klik hier ![]() voor een animatie
van Stelling 4.
voor een animatie
van Stelling 4.
Bewijs:
We zullen, vanwege de "inbedding" van de P-meetkunde in de E-meetkunde, wel
gebruik maken van die "Euclidische" middelen, die eigenschappen van figuren in
de P-meetkunde invariant laten (met name de inversie).
We bekijken allereerst een d-driehoek ABC waarvan C samenvalt met het middelpunt van de
horizon, het d-centrum (zie figuur 7a).
| figuur 7a | 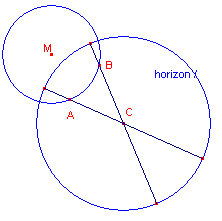 |
figuur 7b | 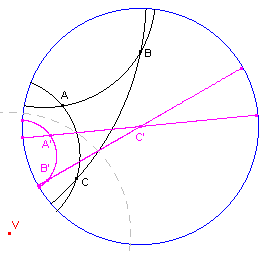 |
Omdat de cirkel M (de drager van de zijde AB van d-driehoek ABC) orthogonaal is met de
horizon, ligt het punt M buiten cirkel C.
De boog AB is dus convex ten opzicht van C.
De som van de hoeken van bij A en B van de d-driehoek ABC is dus kleiner dan de som van de
hoeken bij A en B van de (niet getekende) E-driehoek. Dus kleiner dan 180°.
Indien het hoekpunt C niet samenvalt met het d-centrum passen we een inversie
(die conform is) toe.
Als centrum van inversie kiezen we het punt V (zie figuur 7b), dat het
beeld is van het punt C bij inversie tov. de horizon.
Als inversie cirkel kiezen we de cirkel met middelpunt V die orthogonaal is met de
horizon.
Hierdoor gaat de drager van AC over in de middellijn A'C' van de horizon (C' valt samen
met het d-centrum).
BC gaat over in de middellijn B'C'.
AB wordt afgebeeld op een d-lijn A'B'.
Omdat deze inversie conform is, is de hoekensom van driehoek ABC gelijk aan de hoekensom
van driehoek A'B'C'.
Wegens het eerste deel van het bewijs (C' valt samen met het d-centrum) is de hoekensom
dus kleiner dan 180°.¨
Een direct gevolg van deze stelling is:
| Stelling 5 (P-meetkunde) In een d-driehoek is een buitenhoek groter dan elk van de niet-aanliggende binnenhoeken. |
Bewijs:
Via inversie kan steeds een figuur verkregen worden als in figuur 7a.
Daarbij zijn de hoekgroottes invariant.
Omdat de boog AB convex is tov. C is bijvoorbeeld de p-buitenhoek bij B groter dan de
e-buitenhoek bij B.
Deze e-buitenhoek is groter dan de e-binnenhoek bij A, die evenwel weer groter is dan de
d-binnenhoek bij A.
Dus de d-buitenhoek bij B is groter dan de niet-aanliggende d-binnenhoek bij A.
Eenzelfde bewijs kan worden gegeven voor de andere buitenhoeken. ¨
| Stelling 6 (P-meetkunde) In een d-driehoek is een buitenhoek groter dan de som van de beide niet-aanliggende binnenhoeken. |
Bewijs: (zie figuur 8)
| figuur 8 | 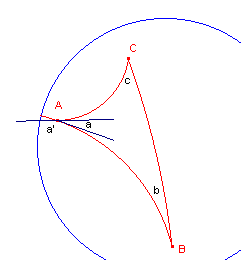 |
In d-driehoek ABC zijn de d-(binnen)hoeken bij A, B en C opvolgend a, b
en c. De buitenhoek bij A (bij verlenging van BA) zij a'. Nu is a + b + c < 180° (zie stelling 4). Verder is a + a' = 180°, zodat a + b + c < a + a' of b + c < a' ¨ |
[hypm2.htm] laatste wijziging op: 03-06-2000