Gelijkvormigheid bij cirkels

Overzicht  ][  Draaivermenigvuldiging | Apollonius-cirkels | Meetkunde

Overzicht terug

  1. Gelijkvormigheidscentra
  2. Gelijkvormigheidscirkel
  3. Machtlijn
  4. Constructie machtlijn

1. Gelijkvormigheidscentra terug
Gegeven zijn twee cirkels (A, a) en (B, b).
Er zijn nu twee punten, S1 en S2, die het centrum zijn van een gelijkvormigheidsafbeelding van de ene cirkel op de andere.
Het ene centrum (S1) wordt wel uitwendig gelijkvormigheidspunt genoemd.
Het is het snijpunt van de centraal van beide cirkels en de lijn door de eindpunten van twee gelijkgerichte stralen van elk van de cirkels.
Het andere centrum (S2) heet inwendig gelijkvormigheidspunt. Het is het snijpunt van de centraal met de lijn door de eindpunten van twee tegengesteld gerichte stralen van beide cirkels.

gelijkv1 Gevolg
De punten S1, S2 en A, B zijn de paren van een harmonisch viertal, immers
(S1,S2,A,B) = AS1/BS1 : AS2 / BS2 = (a/b) : -(a/b) = -1.
[einde Gevolg]

Opmerking
Zie Bijzondere punten van de driehoek: X55 en X56: de gelijkvormigheidscentra van de in- en omcirkel van een driehoek.
[einde Opmerking]

2. Gelijkvormigheidscirkel terug

Stelling 1
Twee cirkels, (A,a) en (B,b) kunnen door oneindig veel draaivermenigvuldigingen (O, j, k) op elkaar worden afgebeeld.
De meetkundige plaats van de punten O is een cirkel, de gelijkvormigheidscirkel van de cirkels A en B.

Bewijs:

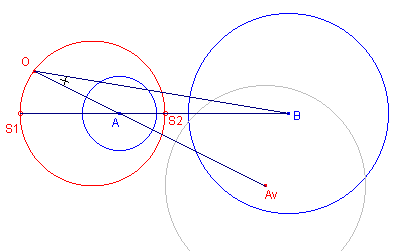gelijkv2 We beelden cirkel A op cirkel B af.
Voor k moet natuurlijk gelden: k = b / a.
De hoek j hangt af van de plaats van het punt O.
O moet zo gelegen zijn, dat OB = k . OA;
zodat OA / OB = 1/k = a / b.
De meetkundige plaats van de punten O is dan de Apollonius-cirkel bij de verhouding a/b.
Deze cirkel gaat door de in- en uitwendige gelijkvormigheidspunten van de cirkels A en B (deze punten zijn tegenpunten van de gelijkvormigheidscirkel). ¨
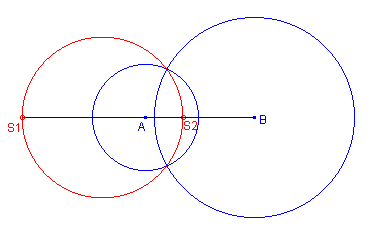gelijkv3 Opmerking
Snijden de cirkels elkaar, dan gaat de gelijkvormigheidscirkel door de snijpunten van de beide cirkels.
[einde Opmerking]

Zie ook "Apollonius-cirkels" en "Draaivermenigvuldiging"

3. Machtlijn terug

We bewijzen allereerst een hulpstelling, betrekking hebbend op inversie.

Stelling 2
Als twee punten van een cirkel elkaars inverse zijn tov. een tweede cirkel, dan zijn die cirkels orthogonaal.

Bewijs:

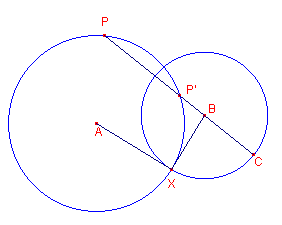gelijkv4 Hiernaast zijn P en P' elkaars inversen tov. de cirkel (B,b).
De punten P en P' zijn beide gelegen op de cirkel (A,a).
Nu zijn B, P en P' collineair (per definitie).
Er geldt:
BP · BP' = b2 = BC2, zodat ook
BP · BP' = BX2
waaruit volgt dat BX raakt aan cirkel A.
Dus AX _|_ BX, hetgeen wil zeggen, dat de beide cirkels orthogonaal zijn. ¨
.
Stelling 3
De inversen van een punt van de gelijkvormigheidscirkel van twee cirkels ten opzichte van die cirkels liggen symmetrisch tov. van de machtlijn van die cirkels.

Bewijs:

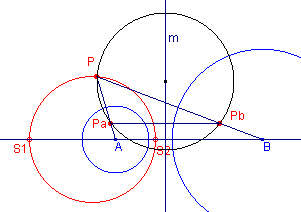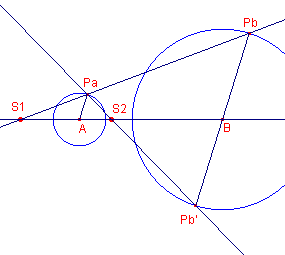
gelijkv5 Hiernaast zijn (A,a) en (B,b) de gegeven cirkels. De cirkel door S1 en S2 is de gelijkvormigheidscirkel van die cirkels.
Pa is het beeld van P bij inversie in de cirkel A; Pb is het beeld van P bij de inversie in de cirkel B.
De lijn m is de machtlijn van de cirkels A en B.
Nu geldt, vanwege de inversie:
AP · APa = a2 ...... (1)
BP · BPb = b2 ...... (2)
Omdat P op de gelijkvormigheidscirkel ligt, is
PA : PB = a : b

Deling van (1) en (2) geeft:
APa / BPb = a / b = PA / PB
waaruit volgt dat PaPb // AB.
De omcirkel van PPaPb is nu orthogonaal met de beide cirkels A en B (volgende bovenstaande hulpstelling).
Het middelpunt van deze omcirkel ligt dus op de lijn m, de machtlijn van de cirfkels.
Zodat ook m _|_ PaPb.
Omdat PaPb een koorde is van de omcirkel, is wordt PaPb door m loodrecht middendoor gedeeld.
Hetgeen bewezen moest worden. ¨

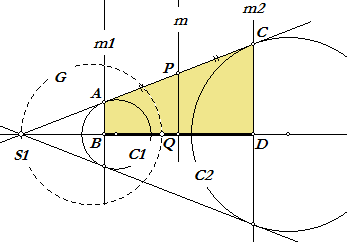gelijkvopm Opmerking. De eigenschap van Stelling 3 geldt natuurlijk ook voor bijvoorbeeld het punt S1 (het uitwendige gelijkvormigheidspunt van beide cirkels).
De inverse punten B en D van S1 bij beide cirkels zijn dan snijpunten van de poollijnen m1 en m2 van S1 bij C1 en C2.
De lijnen m1 en m2 gaan door de raakpunten A en C van een gemeenschappelijke raaklijn aan de cirkels (die ook door S1 gaat).
Het midden P van AC ligt dan op de machtllijn m van de cirkels (immers PA = PC).
En er geldt ook m // m1 // m2.
In trapezium ABDC is dan het snijpunt Q van m met de centraal het midden van het lijnstuk BD.
Waarmee de machtlijn van C1 en C2 de middenparallel is van de lijnen m1 en m2.
Op de eigenschap kunnen we een constructie van de machtlijn m baseren (zie echter paragraaf 4).
(einde Opmerking)
.
 gelijkv6
Gevolg (van Stelling 3)
De poollijn van B tov. cirkel A en de poollijn van A tov. cirkel B liggen symmetrisch tov. de machtlijn van de cirkel A en cirkel B.

 

4. Constructie machtlijn terug
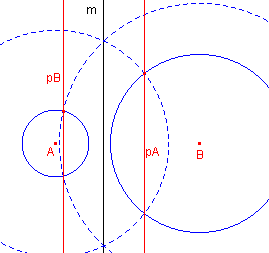
Uit het Gevolg van Stelling 3 kunnen we een eenvoudige constructie afleiden voor de machtlijn van twee cirkels.
Immers, het snijpunt van de machtlijn van (bijvoorbeeld) A met de centraal AB is de inverse van A bij inversie tov. de cirkel B.
En omgekeerd. Zodat:

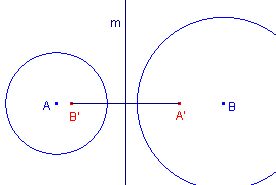gelijkv7
Stelling 4
De machtlijn van twee cirkels is de middelloodlijn van het lijnstuk tussen de inversen elk van de middelpunten van die cirkels tov. de andere cirkel.

Opmerking
Zie ook de constructie op pagina "Macht van een punt"
[einde Opmerking]

begin pagina
[gelijkv.htm] laatste wijziging op: 18-dec-08 (27-2-2003)