Diametraalcirkel, antimacht, antimachtlijn

Overzicht  ][  Macht(lijn) | Meetkunde

Opm. Voor machtlijnen zie ook "Machtlijn van twee cirkels" (Cabri-werkblad) en de pagina "Gelijkvormigheid bij cirkels"

Overzicht terug

  1. Diametraalcirkel, antimacht
  2. Antimachtlijn, antimachtpunt

1. Diametraalcirkel, antimacht terug

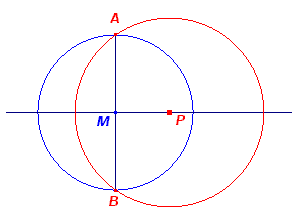antim1 In nevenstaande figuur is (P) een diametraalcirkel van cirkel (M).
Definitie
Een cirkel waarvan een koorde samenvalt met een middellijn van een tweede cirkel, heet diametraalcirkel van die tweede cirkel.
Men zegt ook wel (zie figuur hierboven), dat cirkel (P) de cirkel (M, r) halveert (middendoor deelt).

Gevolg
In driehoek MPA (zie bovenstaande figuur) geldt: PA2 = PM2 + AM2
Of ook
PA2 = PM2 + r2

Definitie
Het kwadraat van de straal van een diametraalcirkel (P) van een cirkel heet de antimacht van P tov. die (gehalveerde) cirkel

Gevolg
Als (P, PA) een diametraalcirkel van (M, r) is, dan is macht(M, cirkel P) = PM2 - PA2 = PM2 - (PM2 + r2) = -r2
[einde Gevolgen]

Stelling 1
De meetkundige plaats van de middelpunten van cirkels die door twee gegeven cirkels gehalveerd worden, bestaat uit het binnen die cirkels gelegend deel van de machtlijn van die gegeven cirkels.

Bewijs:

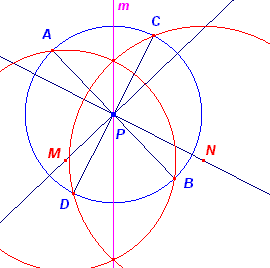antim1a Hiernaast wordt (P, p) gehalveerd door (M, R) en door (N, r).
P kan dan niet buiten die laatste twee cirkels liggen.

De snijpunten A, B van (P) met (M) zijn tegenpunten van (P), evenzo de snijpunten C, D van (P) met (N).
De macht van P tov. elk van die cirkels is dan gelijk aan -p2. P heeft dus gelijke machten tov. (M) en (N).
P ligt dus op de machtlijn m van (M) en (N).
Omgekeerd.
Ligt P op de machtlijn m van (M) en (N). Dan is
m(P,M) = PM2 - R2 = -PA2
m(P,N) = PN2 - r2 = -PC2
Zodat PA = PC (halve koorden).
(P) wordt dus door (M) en (N) gehalveerd.

2. Antimachtlijn, antimachtpunt terug

Stelling 2
De meetkundige plaats van de punten die gelijke antimachten hebben tov twee gegeven cirkels, is een lijn loodrecht op de centraal van die gegeven cirkels.
Deze lijn heet antimachtlijn van de beide gegeven cirkels.

Bewijs:

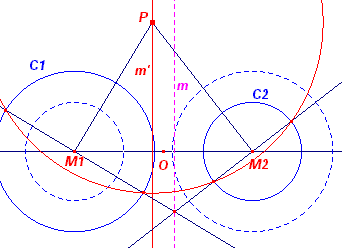antim2 (M1, r1) en (M2, r2) zijn de gegeven cirkels.

P is een punt van de gezochte meetkundige plaats m', als
PM12 + r12 = PM22 + r22
Of:
PM12 - r22 = PM22 - r12
P ligt dus op de machtlijn van de cirkels (M1, r2) en (M2, r1)
Daar deze cirkels ontstaan uit de gegeven cirkels door vermenigvuldiging V met -1 tov het midden O van M1M2, is m' het V-beeld van de machtlijn m van de gegeven cirkels.

Stelling 3
De meetkundige plaats van de middelpunten der diametraalcirkels van twee gegeven cirkels is hun antimachtlijn.

Bewijs:
(zie figuur hierboven)
Voor het middelpunt P van een diametraalcirkel van M1 en M2 geldt dat P gelijke antimachten heeft tov. die cirkels.
P ligt dan op de antimachtlijn.
Omgekeerd, zijn de antimachten van P gelijk, dan is P het middelpunt van een diametraalcirkel.

Stelling 4
De antimachtlijnen van drie cirkels waarvan de middelpunten niet-collineair zijn, zijn concurrent.
Het concurrentiepunt heet het antimachtpunt van de drie cirkels.

Bewijs:

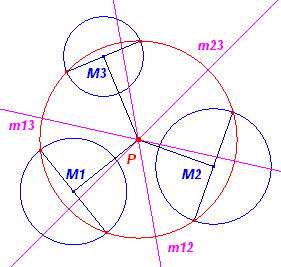antim3 De antimachtlijnen m12 en m13 snijden elkaar in het punt P.
Voor P geldt nu:
am(P, M1) = am(P, M2)
am(P, M1) = am(P, M3)
waaruit volgt:
am(P, M2) = am(P, M3)
P ligt dus ook op de antimachtlijn m23.

Opmerking
P is dus het middelpunt van de gemeenschappelijke diametraalcirkel van de drie gegeven cirkels.
[einde Opmerking]

begin pagina
[antimacht.htm] laatste wijziging op: 31-05-03