Cabri-werkblad
Overzicht ][ Alle werkbladen | Meetkunde | Cabri
Overzicht - Scheve lijnspiegeling
Opdracht 1
Opdracht 2
Opdracht 3 (macro:SchSpiegeling)
Opdracht 4
Opdracht 5
Opdracht 6
Opdracht 7
Opdracht 8
Opdracht 9
Opdracht 10
Opdracht 11
1. Inleiding
Opdracht 1
Teken op een nieuw werkblad een horizontale lijn m en een
driehoek ABC (in het bovenste halfvlak).
Construeer het spiegelbeeld A’B’C’ van driehoek ABC bij spiegeling in de
lijn m (gebruik de functie "Spiegeling", 
in het Afbeeldingen-menu,
het 6e menu van links).
Teken de lijnen AA’, BB’, CC’. Deze lijnen snijden de lijn m
opvolgend in de punten Am, Bm, Cm.
Opdracht 2
 |
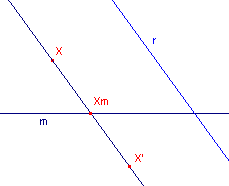Teken op een leeg werkblad opnieuw een (horizontale) lijn m en een lijn r die niet loodrecht staat op m; zie de figuur hiernaast. |
- Beschrijf kort hoe je bij een gegeven punt X het beeldpunt X’ kunt construeren.
- Bewijs: de punten X en X’ hebben gelijke afstand tot de lijn m.
Opmerking
Deze eigenschap zullen we in Opdracht 6 kunnen gebruiken.
De constructie die hierboven is uitgevoerd, noemen we een "scheve spiegeling in
de lijn m in de richting van de lijn r".
We zullen dit vaak kort schrijven als "scheve spiegeling in m(r)"
of ook wel als "lijnspiegeling m(r)".
De lijn m heet ook hier de spiegelas. De lijn r bepaalt de "spiegelrichting".
Opdracht 3 (macro:SchSpiegeling)
Je zal in hetgeen volgt een dergelijke constructie vaker moeten uitvoeren. Het is daarom handig een macro samen te stellen die een scheve spiegeling van een punt uitvoert.
Ga uit van bovenstaande figuur (zie Opdracht 2) en pas de volgende "constructiestappen" toe.
Kies de functie "Beginobjecten",
in het Macro-menu.
Selecteer het punt X, vervolgens de lijn m en dan de lijn r (de volgorde van m en r is belangrijk).
Kies de functie "Eindobjecten",in het Macro-menu.
Selecteer het punt X’.
Kies de functie "Definieer macro",in het Macro-menu.
Geef de macro de naam SchSpiegeling.
Bewaar de macro op disk (selecteer het vakje naast de tekst "Opslaan in bestand").
 |
Construeer met de macro:SchSpiegeling het
beeld A’B’C’ van een driehoek ABC. Opmerking Teken de beide driehoeken met de functie "Driehoek",  .[einde Opmerking]
Ga door verplaatsing van driehoek ABC op het tekenblad na, dat dit ook geldt voor de andere zijden van de driehoeken. Klik hier |
In de meetkunde zijn eigenschappen die bij een afbeelding niet veranderen, van belang (het onderzoeken waard).
Je hebt bij de gewone spiegeling (zie Opdracht 1) gezien, dat driehoek en beelddriehoek congruent zijn; anders gezegd: de lengtes van lijnstukken en de grootte van hoeken veranderen niet (lengte en hoekgrootte zijn invariant).
Bij de scheve spiegeling is dat overduidelijk anders.
Maar ook bij de scheve spiegeling zijn enkele invariante grootheden!
Je hebt er hierboven zelfs al enkele ontdekt (zie Opdracht 2 en Opdracht 4).
Ga uit van de figuur in Opdracht 4.
Kies de functie "Oppervlakte",
in het Reken-menu (3e menu van rechts).Bepaal de oppervlakte van driehoek ABC en die van driehoek A’B’C’.
Als het goed is heb je nu een illustratie van de volgende stelling:
| Stelling Bij een lijnspiegeling m(r) is de oppervlakte van een driehoek invariant. |
We zullen deze invariantie in de volgende opdracht bewijzen.
 |
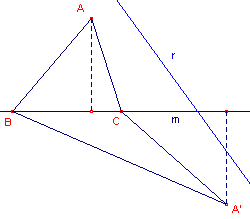Ga eerst uit van een driehoek ABC waarvan de
hoekpunten B en C op de lijn m liggen. We gebruiken de letter ‘V’ om de oppervlakte van een figuur aan te geven.
|
 |
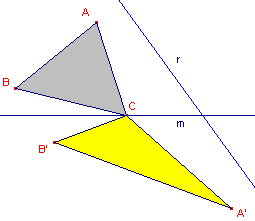Kies vervolgens een driehoek waarvan slechts
één hoekpunt (in dit geval het hoekpunt C) op de lijn m ligt.
|
4. Het beeld van
een cirkel
Opdracht 7
 |
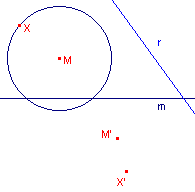Teken op een leeg tekenblad een cirkel met
middelpunt M en willekeurige straal. Kies op de cirkel een punt X (met de functie "PuntOpObject",  in het Punt-menu).Gebruik de macro:SchSpiegeling voor de constructie van de punten M’ en X’.
Gebruik de functie "MeetkundigePlaats", |
in het Constructie-menu, om het beeld van de
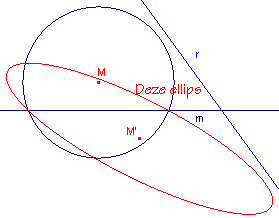
cirkel bij de lijnspiegeling m(r) te bekijken.Het beeld van de cirkel bij de lijnspiegeling m(r) is een ellips.
Verplaats het punt M en wijzig ook de lengte van de straal van de cirkel.
Bekijk daarbij de verandering van de ellips.
Opmerking
Zie ook de CabriJavapplet bij Opdracht 8.
[einde Opmerking]
Een ellips heeft twee symmetrie-assen.
Deze symmetrie-assen gaan door het middelpunt M’ van de ellips.
Probeer de lijnen p en q te vinden (beide gaan door het middelpunt M van de cirkel; waarom?) die als beeld bij de lijnspiegeling m(r) de symmetrie-assen van de ellips opleveren.
Aanwijzing
Verplaats de cirkel zo, dat het punt M samenvalt met het snijpunt van de lijnen m en r.
[einde Aanwijzing]
Construeer de lijnen p en q en de beeldlijnen p’ en q’.
- Geef een (korte) beschrijving van de constructie.
Klik hier 
voor een CabriJavapplet (figuur: schspiegel5a) bij Opdracht
8 (zie eventueel ook Opdracht 7).
 |
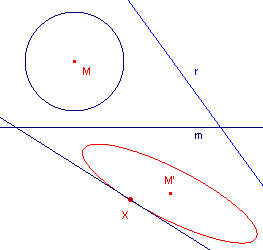
Cabri herkent de meetkundige plaats (zie Opdracht 7) niet als een ellips. Echter, een ellips is bepaald door 5 punten. Kies daarom op de cirkel 5 punten waarvan je ook het beeld bij de lijnspiegeling m(r) bepaalt. Je zou 4 van deze punten kunnen kiezen op basis van hetgeen je in Opdracht 8 hebt gevonden. Gebruik vervolgens de functie "Kegelsnede",  in het Cirkel-menu, om een ellips door de 5
beeldpunten te tekenen. |
- Ga nu met de functie "Oppervlakte" na, dat ook de cirkel en de ellips een gelijke oppervlakte hebben.
 |
Kies op de ellips uit Opdracht
9 een willekeurig punt X (met "PuntOpObject"). Construeer in het punt X een raaklijn aan de ellips.
Klik hier |
De straal van de cirkel geven we aan met R.
De assen van de ellips zijn de delen van de symmetrie-assen die binnen de ellips gelegen zijn. De lengte van de grootste halve as is a; de lengte van de kleinste halve as is b.
Er is een verband tussen R en ab.
- Welk verband is dat?
- Leid daaruit een formule af voor de oppervlakte van een ellips.
5. Download
De meeste figuren van deze pagina, de figuren die gebruikt zijn bij
de CabriJavapplets, en de genoemde macro kunnen in één bestand via
deze website worden gedownload.
Klik hier om het downloadproces te
starten (ZIP-bestand, ca. 12Kb).
Dit werkblad is NIET MEER als PDF-bestand beschikbaar.
[schspiegel.htm] laatste wijziging op: 19-jan-18