Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Kijkhoek

Probleemstelling
Opdracht 1
Op weg naar een constructie
Opdracht 2
Opdracht 3
Constructie
     Opdracht 4a
     Intermezzo
     Opdracht 4b
Naschrift
Download

Probleemstelling
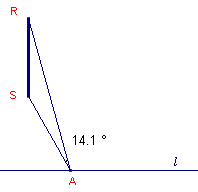
Boven rijstroken op de grote autowegen in ons land hangen op sommige plaatsen (bijna) verticaal verkeersborden. Als je veraf bent is de hoek waaronder je de boven- en onderkant van het bord ziet, de kijkhoek, erg klein. Ook als je er dichtbij (er vlak voor, bijna eronder) bent, is die kijkhoek klein.
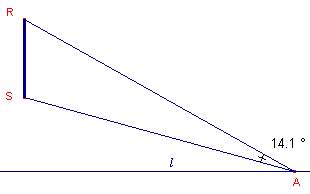
We hebben beide situaties hieronder schematisch weergegeven. A is de positie van een auto op de weg l; RS is het verkeersbord boven de weg, dat we nu echt verticaal hebben geplaatst.

figuur 1		figuur 2

Vraag:

Wat is de positie van de auto (het punt A) waarbij de kijkhoek zo groot mogelijk is.
Opdracht 1

Neem een nieuw tekenblad en neem daarop de gegevens ongeveer als in figuur 1 over.
Het lijnstuk RS staat loodrecht op de horizontale lijn (de weg).
Bepaal de positie van het punt A waarvoor de kijkhoek maximaal is.

Klik hier

voor een CabriJavapplet bij Opdracht 1.

Vermoedelijk heb je de oplossing van Opdracht 1 (gewoon) gevonden door de positie van het punt A op de lijn l te veranderen, aldoor lettend op de grootte van hoek RAS.
Je hebt eigenlijk niets anders gevonden dan een benadering van de positie van A.
Op weg naar een constructie

Het zou "echt" anders geweest zijn, als je gevraagd werd de positie van het punt A op de lijn l te construeren. Immers, construeren houdt ook hier in dat je uitsluitend gebruik maakt van Cabri-functies uit het Teken-, Cirkel- en Constructie-menu (en eventueel het Afbeeldingen-menu).
Opdracht 2

Teken de omcirkel van driehoek RAS (gebruik eventueel de standaard macro:Omcirkel3P).
Zoek nu nog eens naar de grootste hoek door het punt A te verplaatsen op de lijn l.
Valt je bij het vinden van de grootste hoek nu iets op? Zo ja, wat?

Klik hier

voor een CabriJavapplet bij Opdracht 2.

Wellicht heb je ook gevonden, dat
De kijkhoek is maximaal als de omcirkel van driehoek RAS aan de lijn l raakt.
Opdracht 3

Bewijs de conclusie uit Opdracht 2.
Aanwijzing
Probeer eens te bewijzen, dat boog RS dan (als l raakt aan de omcirkel) de grootste boog is op het lijnstuk RS.
Immers, hoek RAS is gelijk aan ….
[einde Aanwijzing]
Constructie

Maar nu de echte constructie nog!
Opdracht 4a

Kijk eens naar figuur 3.

figuur 3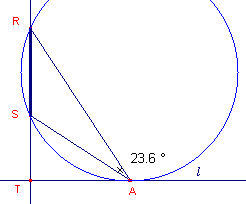

In figuur 3 is de situatie weergegeven waarbij de lijn l aan de omcirkel van driehoek RAS raakt. We hebben ook het snijpunt T van de drager van RS met de lijn l getekend.
Wat weet je nu van het product van de lengtes van de lijnstukken TS en TR?

Klik hier voor een CabriJavapplet bij Opdracht 4a.

Als je dit juist hebt geformuleerd, weet je dat TA middelevenredig is tussen TS en TR.

Intermezzo

figuur 4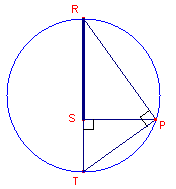

In figuur 4 is een in P rechthoekige driehoek PRT getekend, waarin PS de hoogtelijn is op RT.
De getekende cirkel is de omcirkel van driehoek PRT.
Bewijs nu dat geldt: TP² = TS x TR.
Aan welk lijnstuk in figuur 3 is het lijnstuk TP dus gelijk?

[einde Intermezzo]

Opdracht 4b

Construeer nu het punt A zo op de lijn l, dat hoek RAS maximaal is.
Beschrijf deze constructie kort.
Naschrift

Zie ook de pagina "Maximale kijkhoek" op deze website. Op die pagina wordt met behulp van een functie en diens afgeleide bewezen, dat bij de oplossing van het vraagstuk gebruik gemaakt kan worden van het lijnstuk dat middelevenredig is tussen TR en TS (zie Opdracht 4a hierboven).
Zie ook de pagina "Kijkhoek vanaf een cirkel". Op deze pagina wordt hetzelfde probleem als hierboven behandeld, maar dan als het punt A (het punt van waaruit gekeken wordt) op een cirkel ligt.

Op de pagina "Optimaliseren" van de website van Henk Pfaltzgraff staat een goniometrische oplossing van het probleem met behulp van een programma voor de TI-83, onder de naam "De grootste kijkhoek berekenen".

Download
De figuren op deze pagina kunnen samen met de figuren van de CabriJavapplets via deze website in één bestand worden gedownload.
Klik hier om het downloaden te starten [ZIP-formaat, ca. 9Kb].

Deze pagina is NIET MEERbeschikbaar in PDF-formaat.
kijkhoeks.pdf (ca. 108 Kb)
Een PDF-bestand kan met Acrobat^® Reader worden gelezen:

[kijkhoek.htm] laatste wijziging op: 19-01-18