Een maximaliseringsprobleem [2]

Probleem | Oplossing | Applet | Naschrift ][ Analyse

Zie ook het Cabri-werkblad: Kijkhoek.
Zie ook de pagina "Kijkhoek vanaf een cirkel"

Probleemstelling - Maximale kijkhoek terug
Boven rijstroken op de grote autowegen in ons land hangen op sommige plaatsen (bijna) verticaal verkeersborden. Als je veraf bent is de hoek waaronder je de boven- en onderkant van het bord ziet, de kijkhoek, erg klein. Ook als je er dichtbij (er vlak voor, bijna eronder) bent, is die kijkhoek klein.

We hebben een dergelijke situatie hieronder (zie figuur 1) schematisch weergegeven. A is de positie van een auto op de weg l; RS is het verkeersbord boven de weg, dat we nu echt verticaal hebben geplaatst.

figuur 1 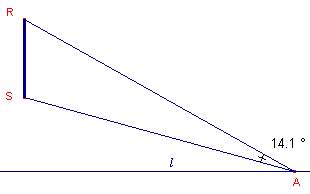kijkhoek1a Vraag:
Wat is de positie van de auto (het punt A) waarbij de kijkhoek zo groot mogelijk is.

Oplossing terug
Zie ook de paragraaf Naschrift.

figuur 2 kijkhoeka2 We brengen een assenstelsel aan met l als x-as en de drager van RS als y-as.
De positie van het punt A op de x-as is nu variabel (zie figuur 2).

Stel OA = x (met x > 0).

Dan is
   tan RAO = OR/OA = OR / x
   tan SAO = OS/OA = OS / x
zodat

   hoek RAS = arctan(OR/x) - arctan(OS/x)

Voor gegeven (positieve) waarden van OR = a en OS = b (met a > b) kunnen we nu de maximale waarde van hoek RAS berekenen.

Zij f(x) = arctan(a/x) - arctan(b/x).
Dan is:
kijkhoekf1
Het tekenschema van f ' is nu voor x > 0:

f '(x) ?+++++++++ 0 ----------
x 0 Ö(ab)

Het maximum vinden we dus voor x = Ö(ab).

De maximale waarde van de hoek is dan arctanÖ(a/b) -arctanÖ(b/a).

Opmerking
Uit x2 = ab volgt, dat x middelevenredig is tussen a en b.
Dit leidt dan tot een meetkundige constructie van de plaats van het punt A (met maximale kijkhoek) op de x-as (de lijn l). Zie de paragraaf Naschrift.
[einde Opmerking]

Applet terug

figuur 3 kijkhoeka3 Figuur 3 is gegenereerd met een CabriJavapplet.
In die figuur is a = 4,00 en b = 0,99.
Uit x2 = ab vinden we x = 1,99 (zie het punt A in figuur 3).

Klik hier Animatie voor het uitvoeren van deze applet.

Opmerking
In figuur 3 is (in rood) de meetkundige plaats getekend van de punten (x, g), waarbij g gelijk is aan de kijkhoek (in graden).
De waarde van g wordt op de y-as gerepresenteerd als y = g/10.
De grafiek is niet de grafiek van de functie f uit paragraaf 2.
[einde Opmerking]

Naschrift terug
Op het Cabri-werkblad "Kijkhoek" wordt een meetkundige behandeling gegeven van het bovenstaande probleem.
Zie ook de pagina "Kijkhoek vanaf een cirkel".

Op de pagina "Optimaliseren" van de website van Henk Pfaltzgraff staat een oplossing van het probleem met behulp van een programma voor de TI-83, onder de naam "De grootste kijkhoek berekenen".
Deze oplossing komt overeen met het hierboven behandelde.

begin pagina

[maxkijkhoek.htm] laatste wijziging op: 24-03-02