Cabri-werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

---

Overzicht - Coördinaten in Cabri

• Inleiding
       Opdracht 1
       Opdracht 2
• Een macro
       Opdracht 3
• Grafieken
       Opdracht 4
       Opdracht 5
• Download

---

Inleiding
Als je een nieuw Cabri-tekenblad kiest, dan gebeurt er op de achtergrond al heel wat, waarvan we (gelukkig?) niets zien.
Eén van die dingen is, dat Cabri (in eerste instantie voor eigen gebruik) een assenstelsel creëert.
Teken je nu bijvoorbeeld een punt op het tekenblad, dan voegt Cabri daaraan direct (en vooralsnog onzichtbaar) de coördinaten toe.
Maar, we kunnen die coördinaten zichtbaar maken en er ook mee werken.
We zullen zien dat Cabri vergelijkingen van lijnen kan bepalen en grafieken van functies kan tekenen.
De Cabri-functies die hierbij gebruikt worden, bevinden zich in twee menu’s: in het Layout-menu ("Toon assenstelsel") en in het Reken-menu ("Vergelijking en coördinaten"); zie figuur 1.

figuur 1
	Layout-menu		Reken-menu

Opdracht 1

Kies dus maar een nieuw tekenblad en teken daarop een punt P.

Ga naar het Layout-menu en kies de functie "Toon assenstelsel"; kies vervolgens in het Reken-menu de functie "Vergelijking en coördinaten".

Selecteer nu het reeds getekende punt P.

Je ziet dan iets als:

figuur 2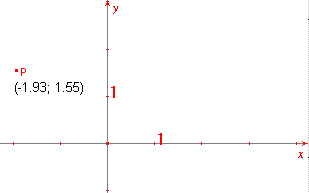

De coördinaten van P hangen af van het zichtbare assenstelsel. Opmerking Het feit, dat de coördinaten in figuur 2 in twee decimalen worden weergeven, is afhankelijk van de (door je docent) gekozen instellingen. [einde Opmerking]

Verplaats nu de oorsprong van het assenstelsel en kijk wat er met de coördinaten van P gebeurt.

Verplaats ook het punt P.

Kijk eens wat er gebeurt als je het punt op de x-as dat met een 1 is aangegeven (Deze eenheid), naar rechts of naar links verplaatst. Geef een korte beschrijving.

Opdracht 2

Teken op hetzelfde tekenblad nu ook een punt Q.

Teken de lijn door P en Q.

Kies nu in het Reken-menu weer "Vergelijking en coördinaten" en selecteer dan de lijn PQ.

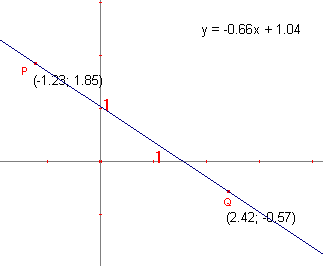
Cabri bepaalt nu dus de vergelijking van de lijn ten opzichte van het weergegeven assenstelsel (zie figuur 3a).

figuur 3a		figuur 3b

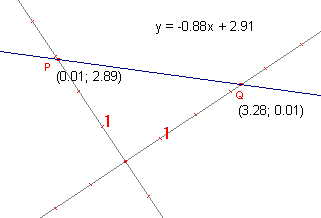• Verplaats nu het punt Q zo, dat PQ loodrecht staat op de y-as.
• Kan je aan de vergelijking zien, dat er inderdaad sprake is van loodrechte stand? Verklaar je antwoord.
• Verplaats nu het punt P zo, dat PQ loodrecht staat op de x-as.
• Kan je aan de vergelijking zien, dat er sprake is van loodrechte stand? Verklaar je antwoord.
• Verplaats nu de oorsprong horizontaal en/of verticaal.
• Welke waarde in de vergelijking van de lijn blijft nu onveranderd? Waarom is dat?
• Selecteer nu de x-as (Deze assen), houd je linker muisknop ingedrukt en draai de as in tegenwijzerrichting (zie figuur 3b).
• Verklaar nu waarom beide getallen in de vergelijking van de lijn PQ veranderen.

Een macro

In het Layout-menu staat nog een functie die we kunnen gebruiken als we met een assenstelsel werken: "Definieer rooster" (zie figuur 4a).

figuur 4a		figuur 4b
Layout -menu		Constructie -menu

Opdracht 3

Alleen als je een assenstelsel hebt gekozen (gedaan met "Toon assenstelsel"), kan je de functie "Definieer rooster" gebruiken.

Kies de functie "Definieer rooster" en selecteer daarna (klik op) éen van de assen van het assenstelsel (Deze assen).

Alle punten met gehele coördinaten worden nu op het tekenblad zichtbaar. Dit zijn dus de roosterpunten.

• Kies in het Punt-menu de functie "Punt".
• Beweeg dan de Wijzer over het tekenblad. Wat merk je op, als je met de Wijzer in de buurt van een roosterpunt komt?
• Teken het punt met coördinaten (3 ; 1).

Het is niet mogelijk op deze manier het punt met coördinaten (3½ ; 1½) te tekenen. Immers dat is geen roosterpunt.

We zullen voor deze toepassing een macro ontwerpen.

• Kies een nieuw tekenblad en maak het assenstelsel zichtbaar ("Toon assenstelsel").
• Gebruik de functie "Wijzig getallen" in het Extra-menu om twee getallen (voor de x- en y-coördinaat van het te tekenen punt) op het tekenblad te zetten (zie figuur 5: de getallen 3.5 en 1.5).

figuur 5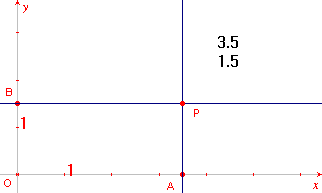

Aanwijzing
Na het kiezen van de functie moet je ergens op het tekenblad klikken; dan opent zich een speciaal venstertje, , waarin je "drie punt vijf" typt.
Daarna klik je op een andere plaats op het tekenblad en je typt "1.5" in eenzelfde venstertje.
[einde Aanwijzing]

We leggen nu de x-coördinaat op de x-as vast met de functie "Maat overbrengen" uit het Constructie-menu (zie figuur 4b).

• Kies deze functie, selecteer het getal 3.5 en klik daarna op de x-as. Op de x-as staat nu een punt (A in figuur 5) op de positie 3,5.
• Doe hetzelfde met het getal 1.5 (zie het punt B in figuur 5).
• Teken nu een loodlijn door A op de x-as, en een loodlijn door B op de y-as.

Het snijpunt van beide loodlijnen is het punt P.

Je kan nu de macro:PuntCoord vastleggen.

• Kies in het Macro-menu de functie "Beginobjecten".
• Selecteer het getal 3.5 (Dit getal), dan het getal 1.5 en tenslotte éen van de assen (Deze assen).
• Kies in het Macro-menu de functie "Eindobjecten".
• Selecteer het punt P.
• Kies in het Macro-menu de functie "Definieer macro".
• Bewaar de macro op disk (aangeven bij "Opslaan in bestand").

Opmerking

We zullen deze macro in Opdracht 4 gebruiken.
[einde Opmerking

Grafieken
De methode die hierboven is weergegeven, kunnen we, enigszins gewijzigd, ook gebruiken om grafieken van functies te tekenen.
Kortweg gezegd:
een functie is een voorschrift waarmee bij een (willekeurige) waarde van x de bijbehorende waarde van y wordt vastgelegd.
De "meetkundige plaats" van alle punten (x, y) is dan de grafiek van de functie.

Opdracht 4

We willen nu de grafiek tekenen van y = ½x² + 1/x.

• Kies een nieuw tekenblad met daarop het assenstelsel. Zorg ervoor, dat de macro:PuntCoord beschikbaar is.

Kies nu een willekeurig punt X op de x-as (met "Punt op object"; Op deze as).

Toon de coördinaten van dat punt (met de functie "Vergelijking en coördinaten").

De x-waarde van het punt X gebruiken we om met de "Rekenmachine" (zie ook het Cabri-werkblad "Rekenmachine") de bijbehorende y-waarde te bepalen.

• Voer de bedoelde berekening met Cabri’s Rekenmachine uit (zie figuur 6).

figuur 6

Opmerking Selecteer telkens als de waarde van x nodig is, de x-coördinaat van het punt X, die door Cabri geplaatst is in de variabele a. [einde Opmerking]

De y-waarde zetten we, na het klikken op de knop [=] van de Rekenmachine, op het tekenblad (klik op de uitkomst en dan op de gewenste positie op het tekenblad).

Kies nu de macro:PuntCoord; deze staat onderaan in het Macro-menu.

Selecteer de x-coördinaat van het punt X (Dit getal), selecteer dan het getal achter "Resultaat:" en klik tot slot op éen van de assen.

Het punt met coördinaten (x, y) wordt dan op het tekenblad geplaatst (zie punt Y in figuur 7).

figuur 7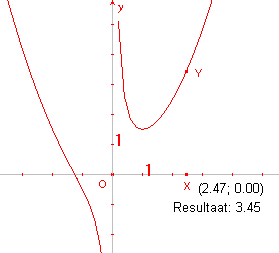

Kies dan de functie "Meetkundige plaats" in het Constructie-menu. Selecteer het punt Y en vervolgens het punt X. De door Cabri getekende meetkundige plaats is de grafiek van de functie y = ½x2 + 1/x.

Opdracht 5

a.	Teken in dezelfde figuur ook de grafiek van y = ½x2.
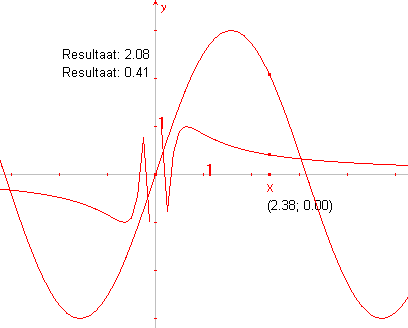
b.	Teken ook de grafieken van de functies y = 3 sin x en y = sin(1/x) in éen figuur (zie figuur 8a).

.

figuur 8a		figuur 8b

De grafiek van y = sin(1/x) heeft in de buurt van x = 0 een wat eigenaardig gedrag.
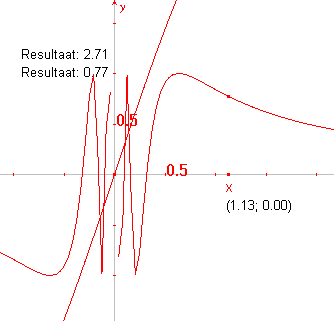Je kan daarin wat meer inzicht krijgen, als je de grafiek vergroot.
Dat kan door verplaatsing van de eenheid op de x-as.

c.	Selecteer het punt op de x-as dat is aangegeven met 1 (Deze eenheid). Sleep dit punt wat meer naar rechts (zie figuur 8b). Opmerking Tijdens het verslepen van de eenheid wijzigt de waarde! [einde Opmerking]
d.	Experimenteer ook eens met enkele andere functies (naar eigen keuze).

---

Download
Dit werkblad is NIET MEER in PDF-formaat beschikbaar.
coords.pdf (ca. 420 Kb)
Een PDF-bestand kan met Acrobat^® Reader worden gelezen:

---

[coord.htm] laatste wijziging op: 19-01-18