Overzicht ][ Alle werkbladen | Meetkunde | Cabri
0. Overzicht - Cabri's rekenmachine
- Inleiding
Opdracht 1
- Wijzigen van de uitdrukking
Opdracht 2 - Gebruik van de functietoetsen
Opdracht 3
Opdracht 4 - Sinus-functie
Opdracht 5 - Download
1. Inleiding
In het Reken-menu van Cabri (het derde menu van rechts) vinden we de functie "Rekenmachine":
Met behulp van deze (beperkte) rekenmachine kunnen we berekeningen uitvoeren, waarvan
het resultaat op het Cabri-werkblad kan worden geplaatst.
We werken eerst een eenvoudige opdracht uit.
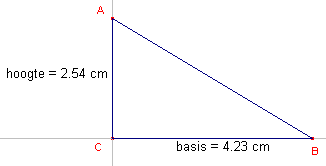
| a. | Teken een rechthoekige driehoek ABC en meet daarvan de
lengte van de beide rechthoekszijden. Aanwijzing Teken eerst twee lijnen die in C loodrecht op elkaar staan. Kies de punten A en B op deze lijnen met de functie "Punt op object". Je hoeft de lijnstukken CA en CB niet te tekenen (maar het mag wel). Kies dan de functie "Rekenmachine". |
In het grote venster (we noemen het in hetgeen volgt "rekenvenster") van de
Rekenmachine kunnen uitdrukkingen worden geplaatst. Dat kunnen getallen zijn, maar ook
getalwaarden die op het werkblad staan (zoals de lengtes van de beide rechthoekszijden).
Deze getalwaarden worden door Cabri zelf toegevoegd aan variabelen (aangegeven met
letters: a tot en met z).
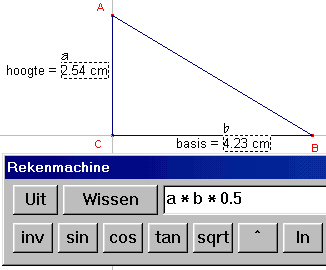
| b. | Klik om te beginnen in het rekenvenster (hiermee maak je
de rekenmachine actief). Selecteer nu de waarde van de hoogte (je ziet dan "Dit getal"). Op het werkblad wordt dan boven het getal de variabele zichtbaar (een a). Deze a zie je ook terug in het rekenvenster. Klik dan op de [x] toets van de rekenmachine en selecteer dan de lengte van de basis (nu wordt de variabele b gebruikt). Klik dan weer op [x] en type vervolgens 0.5 (nul punt vijf). |
We hebben dan
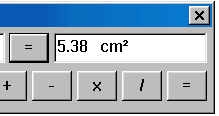
| c. | Klik nu op de [=] knop van de Rekenmachine (of gebruik de
[Enter] toets). Het antwoord van de uitdrukking komt dan in het antwoordvenster. Klik vervolgens op het antwoord en beweeg de wijzer nu naar het werkblad. Kies daarop een positie en klik met de linker muisknop. Het antwoord wordt nu (achter de tekst "Resultaat:") op het werkblad geplaatst. |
| . |
 |
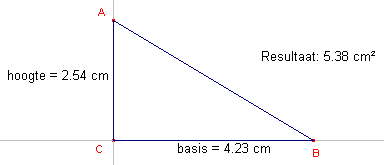Nb. De tekst "Resultaat:" kan worden gewijzigd. |
| . |
| d. | Ga na, door verplaatsing van de punten A en B, dat het resultaat van de berekening wordt aangepast. |
voor een CabriJavapplet bij Opdracht 1.
2. Wijzigen van de
uitdrukking
De rekenkundige uitdrukking waarop een resultaat is gebaseerd, kan ook worden gewijzigd.
Ga daartoe als volgt te werk.
Opdracht 2
| a. | Kies de functie "Rekenmachine" en klik in het rekenvenster. |
| b. | Dubbelklik nu op het getal achter
"Resultaat:". Je ziet dan de gebruikte uitdrukking weer in het rekenvenster (de gebruikte variabelen worden eveneens op het werkblad aangegeven). Wijzig nu het getal 0.5 in bijvoorbeeld 120/240 en bekijk het gevolg. |
3. Gebruik van de functietoetsen
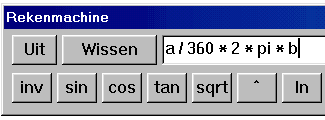
De functietoetsen op de Rekenmachine spreken wel voor zichzelf.
De toets [inv] bepaalt de inverse van de functies [sin], [cos], [tan], [ln] en [log]; de inverse functies zijn opvolgend arcsin, arccos, arctan, exp(x) = ex, 10^(x) = 10x.
Je moet bij het gebruik van haakjes ook de afsluitende haakjes gebruiken.
Voorkomende foutmeldingen hierbij zijn:
Er is een fout gevonden bij de analyse van de uitdrukking
Deling door 0.
Ga weer uit van bovenstaande rechthoekige driehoek (zie Opdracht 1).
| a. | Meet de hoeken bij A en B. |
| b. | Bereken daarna met de Rekenmachine sin2A+cos2A. |
| c. | Bepaal met Cabri de lengte van de zijde AB. |
| d. | Controleer Cabri’s lengteberekening met de stelling van Pythagoras (gebruik ook nu de Rekenmachine; in één uitdrukking?). |
| e. | Bereken ook: ½ AB·BC·sinB. Klopt dit met een eerder berekend resultaat? |
| a. | Waaruit kan je afleiden dat de goniometrische functies van
Cabri werken met graden? De reden daarvan is, dat het in de meetkunde gebruikelijk is de grootte van hoeken uit te drukken in graden. |
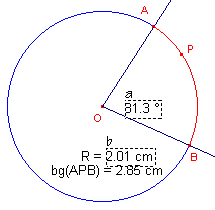
Er is een verband tussen de grootte van de middelpuntshoek AOB van een cirkel en de bijbehorende boog APB.
| b. | Welk deel van de totale omtrek van de cirkel is een boog bij een hoek van x°? |
In bovenstaande figuur is de boog AB bepaald via het punt P. De lengte van de boog (en van de straal R) is berekend met de functie "Afstand en lengte".
| c. | Levert de uitdrukking die in het rekenvenster (zie boven) staat, nu ook de gewenste lengte (in cm)? |
voor een CabriJavapplet bij Opdracht
4c.
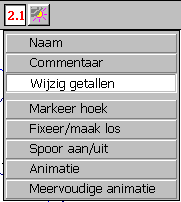
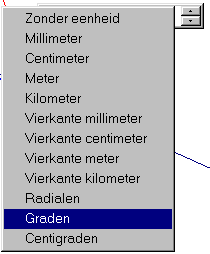
| d. | Kies de functie "Wijzig getallen" in het Extra-menu,
en klik op het werkblad. Het is nu (oa.) mogelijk een getal dat is voorzien van
eenheden, op het werkblad te plaatsen. Type 360 en druk op [Ctrl+U] (dit betekent:
houd de control-toets ingedrukt en druk dan op de U-toets. Geheugensteuntje: de U van
"unit"). Er verschijnt dan een menu waarin je "Graden" kiest (zie boven). |
| e. | Voer hierna nog eens een berekening uit als in onderdeel c. die de lengte van boog APB oplevert. |
| f. | Bereken op dezelfde manier de oppervlakte van het vlakdeel (de sector) OAPB. Je kan daarbij ook de functie "Oppervlakte" uit het Reken-menu gebruiken voor de oppervlakte van de cirkel. |
Opdracht 5
In onderstaande figuur zijn de lengtes van OP en PQ vastgesteld met de functie "Afstand en lengte".
Hoek AOP is omgerekend naar radialen.
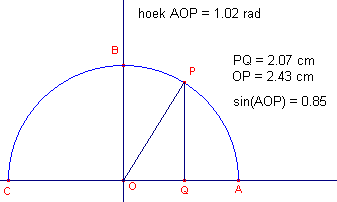
De sinus van hoek AOP, in de figuur geschreven als sin(AOP), is berekend volgens de definitie van de sinus (PQ/OP).
| a. | Kies een nieuw werkblad en maak daarop bovenstaande
figuur, inclusief alle teksten. Opmerkingen De halve cirkel is geconstrueerd door middel van cirkelboog ABC. P is een punt van die boog ("Punt op object"). Enkele noodzakelijke gegevens zijn op het werkblad verborgen (met de functie "Verberg/toon" uit het Layout-menu). |
| b. | Geef aan welke elementen op het werkblad zijn verborgen. |
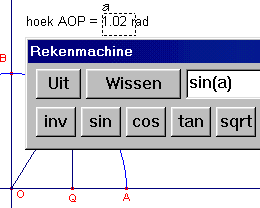
| c. | Zoals uit de laatste figuur blijkt, is nu de grootte van
hoek AOP in radialen in het rekenvenster geplaatst (zie het gebruik van de
variabele a). Welke waarde geeft Cabri nu voor sin(AOP)? Geef een mogelijke verklaring van het resultaat. |
voor een CabriJavapplet bij Opdracht
5c.
5. Download
Dit werkblad is NIET MEER beschikbaar in
PDF-formaat.
cabricalc.pdf (ca. 365 Kb)
Een PDF-bestand kan met Acrobat® Reader worden gelezen: 
Ook de op deze pagina gebruikte figuren kunnen in een
bestand worden gedownload.
Klik hier om het downloaden te starten (ca.
3Kb, ZIP-formaat).
[calc.htm] laatste wijziging op: 19-01-18