Cabri-FAQ (23)

Vorige

Begin

Volgende

Vraag 23
Waarom heeft een meetkundige plaats soms een "vreemde" vorm?

Antwoord

Meetkundige plaatsen worden door Cabri (standaard) benaderd met een gebroken lijn. De nauwkeurigheid van die benadering wordt vastgelegd door het aantal deelpunten van die gebroken lijn. De standaard waarde in Cabri is 50 punten (Windows) of 30 punten (Mac).
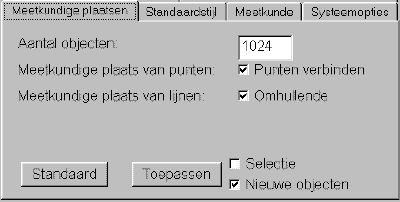
Het aantal deelpunten (objecten) kan worden gewijzigd in het menu Opties | Voorkeuren | Meetkundige plaatsen (zie figuur).
Er kan dan tevens worden aangegeven of de wijziging van toepassing moet zijn op de geselecteerde en/of op de nieuw te construeren meetkundige plaatsen (objecten).

Indien het opgegeven aantal deelpunten "klein" is, kan een meetkundige plaats een niet verwachte gedaante krijgen (zie figuur 23a).
Hoe groter het aantal deelpunten is, des beter is de benadering van de meetkundige plaats.

Voorbeeld

figuur 23a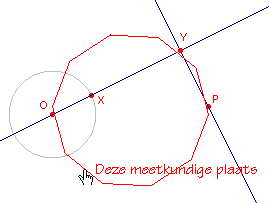

figuur 23b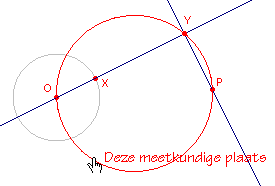

De lijn OX draait (via het punt X) om het punt O.
Y is het voetpunt van de loodlijn op OX uit het punt P.
De meetkundige plaats van Y getekend, in figuur 23a op basis van 10 deelpunten; in figuur 23b op basis van 50 deelpunten.

[einde Voorbeeld]

Daarnaast kan het voorkomen, dat een meetkundige plaats "limietpunten" (eindig of oneindig) heeft of discontinuïteiten vertoont. In zo'n geval wordt soms het eerste punt met het laatste punt (bij limietpunten) of het "linker" met het "rechter" discontinuïteitspunt door een deellijnstuk verbonden.
Dit kan in ieder geval worden voorkomen door in het menu Opties | Voorkeuren de optie "Punten verbinden" Uit te zetten (zie figuur hierboven).
In dit geval moet het aantal deelpunten "groot" worden gekozen om een goede indruk te krijgen van de meetkundige plaats.

Voorbeelden
[1]

figuur 23c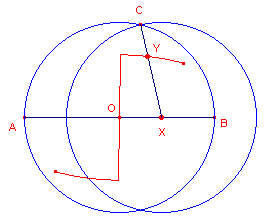

figuur 23d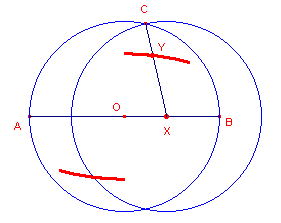

X is een punt van het lijnstuk AB (met midden O).
De cirkels O(OA) en X(OA) snijden elkaar in een punt C. Het punt Y ligt "ergens" op het lijnstuk XC.
De meetkundige plaats van het punt Y (bij variabele X) is in figuur 23c weergeven met de optie Verbinden Aan. In figuur 23d staat die optie Uit.

Opmerking
De constructie in dit voorbeeld vormt de basis van een ellipsconstructie (de Ellipsograaf van Van Schooten).
[einde Opmerking]

[2]

figuur 23e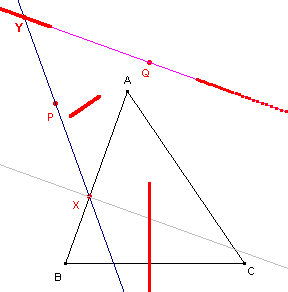

figuur 23f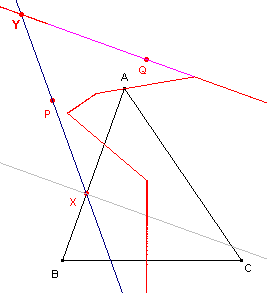

Op de omtrek van driehoek ABC ligt een variabel punt X.
Door het punt Q gaat een lijn die evenwijdig is met de loodlijn in X op de zijde (waarop X ligt).
Y is het snijpunt van de lijn PX met deze lijn.
In figuur 23e is de meetkundige plaats van Y getekend met de optie "Punten verbinden" Uit.
In figuur 23f staat die optie Aan.

Klik hier voor een CabriJavapplet bij figuur 23e (niet-verbonden punten).
Klik hier voor een CabriJavapplet bij figuur 23f (verbonden punten).
[einde Voorbeelden]

Zie Download

Vorige

Begin

Volgende

[faq23.htm] laatst wwijziging op: 09-07-01