Ruimtemeetkunde - Enkele (basis)stellingen

Overzicht ][ Axioma's | Definities | Overzicht stereo

Overzicht

Hieronder volgen enkele eigenschappen (min of meer direct volgend uit de axioma's) die gerekend kunnen worden tot de basisstellingen van de ruimtemeetkunde.
Voor eigenschappen van andere figuren wordt verwezen naar de pagina "Overzicht stereo".

St 1:	Door een lijn l en een niet daarop gelegen punt P gaat precies één vlak.	.		St 6:	*(Drievlaksstelling)* Als drie vlakken U, V, W drie snijlijnen hebben, dan gaan die snijlijnen door hetzelfde punt OF zijn alle drie evenwijdig.
St 2:	Door twee snijdende rechten l en m gaat precies één vlak.		.	St 7:	Als twee snijdende rechten in een vlak evenwijdig zijn met twee rechten in een ander vlak, dan zijn die vlakken evenwijdig.
St 3:	Door twee evenwijdige rechten l en m gaat precies één vlak.		.	St 8:	Als twee rechte lijnen beide evenwijdig zijn met een derde rechte lijn, dan zijn ze evenwijdig met elkaar.
St 4:	Als twee evenwijdige vlakken V en W gesneden worden door een derde vlak U, dan zijn de snijlijnen l en m van die vlakken evenwijdig.		.	St 9:	*(Drie-lijnen-stelling)* Als drie lijnen die niet in hetzelfde vlak liggen, elkaar snijden dan gaan ze door hetzelfde punt.
St 5:	Als l // V en W is een vlak door l dat V snijdt, dan is l evenwijdig met de snijlijn s van V en W.		.

Stelling 1
Door een lijn l en een niet daarop gelegen punt P gaat precies één vlak.

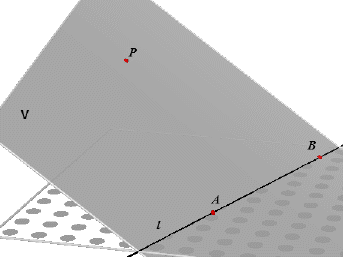Bewijs. Kies op de lijn l twee verschillende punten A en B. Volgens Axioma 2 (Door drie vrijgelegen punten gaat precies één vlak) bepalen deze punten samen met het gegeven punt P precies één vlak.

Stelling 2
Door twee snijdende rechten l en m gaat precies één vlak.

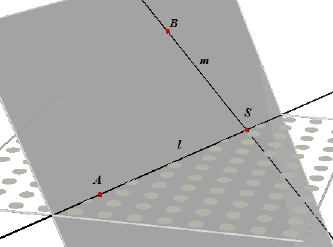Bewijs. Kies op l een punt A en op m een punt B. Samen met het snijpunt S van de lijnen bepalen die punten dus precies één vlak (Stelling 1).
Volgens Axioma 3 (een rechte lijn waarvan twee punten in een vlak liggen, ligt geheel in dat vlak) liggen de lijn l en de lijn m geheel in dat vlak.

Stelling 3
Door twee evenwijdige rechten l en m gaat precies één vlak.

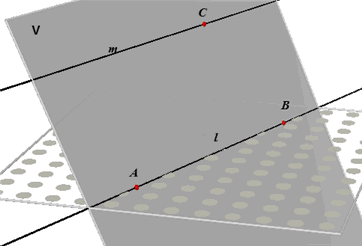Bewijs. Per definitie liggen de lijnen l en m in hetzelfde vlak V. Stel er is een tweede vlak W door l en m. Kies nu in dat vlak W op l de punten A en B en op m het punt C. Volgens Axioma 1 vallen de vlakken V en W dan samen.

Stelling 4
Als twee evenwijdige vlakken V en W gesneden worden door een derde vlak U, dan zijn de snijlijnen l en m van die vlakken evenwijdig.

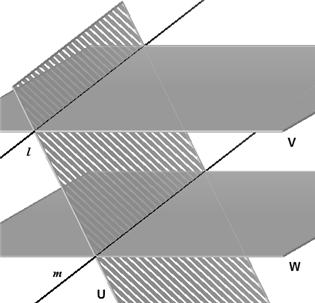Bewijs. De lijnen l en m liggen in ieder geval in hetzelfde vlak U.
Er zijn nu slechts twee mogelijkheden:
(1) l en m snijden elkaar, of
(2) l en m zijn evenwijdig.

(Bewijs uit het ongerijmde) Als de lijnen elkaar zouden snijden in het punt S (mogelijkheid 1), dan ligt S ook in vlak V en ook in vlak W. Die vlakken zijn dan niet evenwijdig.
Dus in dit geval: tegenspraak met het gegeven dat V en W evenwijdige vlakken zijn.

De lijnen l en m zijn daarmee evenwijdig.

Stelling 5
Als l // V en W is een vlak door l dat V snijdt, dan is l evenwijdig met de snijlijn s van V en W.

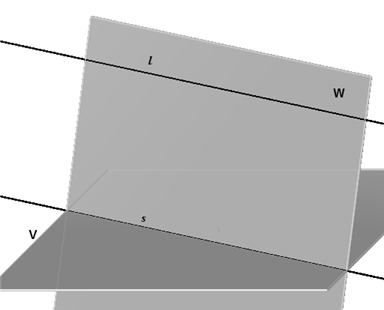Bewijs. Er zijn drie mogelijkheden:
(1)   l kruist s;
(2)   l snijdt s:
(3)   l // s.

Ad (1). Dit is onmogelijk, omdat l en s in hetzelfde vlak W liggen.
Ad (2) De lijnen l en s liggen beide in W. De lijn l snijdt s niet, omdat l geen punt gemeenschappelijk heeft met V en s in het vlak V ligt.

Blijft over: (3) l // s.

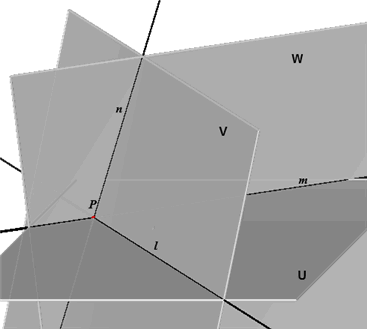
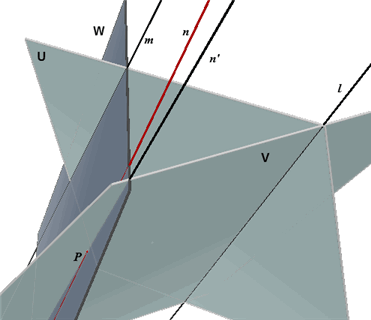
Stelling 6 (Drievlaksstelling)
Als drie vlakken U, V, W drie snijlijnen hebben, dan gaan die snijlijnen door hetzelfde punt OF zijn alle drie evenwijdig.

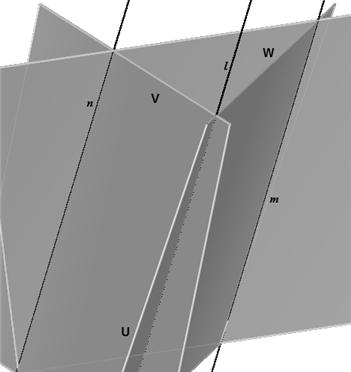Bewijs. U&V = l, U&W = m, V&W = n.

Omdat de snijlijnen twee aan twee in een vlak liggen, is het uitgesloten dat twee snijlijnen elkaar kruisen.

(1)
Stel nu dat de lijnen l en m elkaar snijden in het punt P (zie linker figuur).
Het punt P ligt dan op l, en dus ook in V en op m en dus ook in W.
Het punt P ligt daarmee dus op de snijlijn n van de vlakken V en W.
De lijnen l, m, n gaan dan door hetzelfde punt, namelijk door P.

(2)
Blijft alleen over het geval dat geen twee van de drie lijnen elkaar snijden (zie rechter figuur). Omdat de snijlijnen elkaar ook niet kruisen, zijn ze evenwijdig. Dus l // m, l //n en m // n.

Opmerking. Het punt P wordt wel eens het drievlakspunt of drievlakkenpunt van U, V, W genoemd.
De Drievlaksstelling (en ook het drievlakspunt) wordt gebruikt bij de constructie van doorsneden van ruimtelijke lichamen met een plat vlak.
Zie ook Stelling 9, Drie-lijnen-stelling).
[einde Opmerking]

¤ Zie ook Cabri3D applets:
Drie vlakken en hun snijlijnen (1) - klik hier >< (opent in een nieuw Venster / Cabri3D plug-in noodzakelijk)
Drie vlakken en hun snijlijnen (2) - klik hier >< (opent in een nieuw Venster / Cabri3D plug-in noodzakelijk)

Klik hier >< om beide Cabri3D-figuren te downloaden (ZIP-bestand, ca. 15 Kb).

Stelling 7
Als twee snijdende rechten in een vlak evenwijdig zijn met twee rechten in een ander vlak, dan zijn die vlakken evenwijdig.

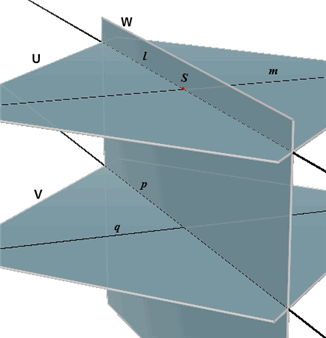Bewijs. De lijnen l en m in het vlak U snijden elkaar in S. Voor de lijnen p en q in V geldt dat p // l en q // m.

(Bewijs uit het ongerijmde) Veronderstel dat de vlakken U en V een snijlijn s hebben.
We brengen nu een vlak W aan door de evenwijdige lijnen p en l. De drie vlakken U, V, W hebben nu drie snijlijnen, waarvan er twee, namelijk p en l, evenwijdig zijn. Volgens Stelling 6 geldt dan voor de lijn s: s // l.
Op dezelfde manier is aan te tonen dat ook s // m.
Maar de snijdende lijnen l en m kunnen niet beide evenwijdig zijn met s. De veronderstelling dat U en V elkaar snijden leidt dus tot een tegenspraak.

Dus: U // V.

Stelling 8

Als twee rechte lijnen beide evenwijdig zijn met een derde rechte lijn, dan zijn ze evenwijdig met elkaar.

Bewijs. Er is gegeven: l // m en m // n; we willen bewijzen dat l // n.

We brengen nu drie vlakken aan:
-  U door l en m ;
-  V door m en n ;
-  W door m en een punt P op n.
Deze drie vlakken hebben drie snijlijnen, namelijk l, m en n' = V&W waarvan er twee evenwijdig zijn (te weten l en m).
Merk op dat P ook gelegen is op de lijn n' (immers P ligt in V, namelijk op n, en n ligt in W).
Volgens Stelling 6 zijn de lijnen l, m en n' evenwijdig, en dus is n' // m (en n' // l).
Maar gegeven is dat ook n // m.
Door het punt P gaat er slechts één lijn die evenwijdig is met m. De lijnen n' en n vallen dus samen.
Met andere woorden: l // n.

Stelling 9 (Drie-lijnen-stelling)

Als drie lijnen die niet in hetzelfde vlak liggen, elkaar snijden dan gaan ze door hetzelfde punt

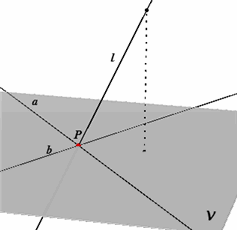Gegeven: a snijdt b in het punt P, b snijdt l en l snijdt a. De lijnen a, b, l liggen niet in hetzelfde vlak
Te bewijzen: ook l gaat door P.
Bewijs. Door a en b wordt het vlak V bepaald. De lijn l ligt niet in het vlak V.
Voor de lijn l zijn er nu 2 mogelijkheden:
(1) l snijdt a in A en b in B waarbij A en B verschillend zijn;
(2) l snijdt a en b in het punt P.
Ad (1). Nu heeft l twee verschillende punten (A en B) met V gemeenschappelijk. Volgens Axioma 3 ligt l dan in V. Dit is in tegenspraak met het gegeven.
Dus mogelijkheid (2) blijft over: l snijdt a en b in het punt P.

Gevolg. Als er meer dan drie lijnen zijn die elkaar twee aan twee snijden (en niet in hetzelfde vlak liggen), dan zijn er zeker drie lijnen a, b, l te vinden die niet in hetzelfde vlak liggen). Alle lijnen die a, b, l snijden gaan nu door P, want zou er een lijn m zijn die a en b in verschillende punten snijdt, dan moet m in V liggen en zouden l en m kruisende lijnen zijn (tegenspraak).

[p: stellingen.htm] laatste wijziging op: 15-10-2008 (05-10-2008)