Omgeschreven bol van een viervlak

Zie ook : De bol
Zie ook : Ingeschreven bol van een viervlak

Stelling
Door vier punten A, B, C, D die niet in hetzelfde vlak liggen, gaat precies één bol (de omgeschreven bol van viervlak ABCD).

Bewijs:

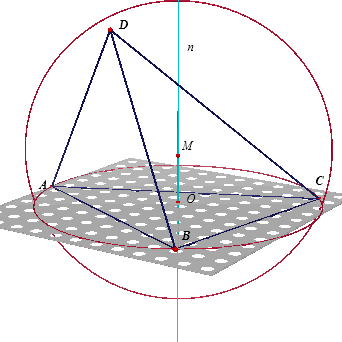ABCD is een viervlak.

De middelpunten van de bollen door A en B liggen in het middelloodvlak van het lijnstuk AB.
De middelpunten van de bollen door B en C liggen in het middelloodvlak van het lijnstukBC.
Beide vlakken snijden snijden elkaar volgens de lijn n (de as van de omcirkel van driehoek ABC; middelpunt daarvan is het punt O, het snijpunt van n met vlak ABC).
De lijn n is de meetkundige plaats van de middelpunten van de bollen door A, B, C.
Het middelloodvlak van (bijvoorbeeld) het lijnstuk CD snijdt n in het punt M.
Het punt M is het middelpunt van de bol door A, B, C, D.

Dat de lijn n het middelloodvlak van CD snijdt is vanzelfsprekend. Was dit namelijk niet het geval, dan zou het middelloodvlak van CD loodrecht op vlak ABC staan en CDzou dan in vlak ABC liggen.

Er is dus steeds een punt M op gelijke afstand van A, B, C, D.¨

Klik hier >< voor een Cabri 3D applet () die het bovenstaande, via drie middelloodvlakken, illustreert (opent in een Nieuw venster).
Klik hier >< voor een Cabri 3D applet waarin de doorsneden met de zijvlakken zijn opgenomen (opent in een NieuwVenster).

Opmerking
De zes middelloodvlakken van de ribben van het viervlak snijden elkaar drie aan drie volgens de as van de omcirkel van een zijvlak.
De vier assen van het viervlak ABCD gaan dus alle door het punt M.
Klik hier >< voor een Cabri 3d applet met de vier assen van een viervlak ABCD (opent in een NieuwVenster).
[einde Opmerking]

[p : ombol.htm] laatste wijziging op: 14-09-2008