De bol
Definitie en hoofdeigenschap | Twee bollen ][ Overzicht stereo | Cabri 3D
Zie ook : Omgeschreven bol van een viervlak
Zie ook : Ingeschreven bol van een viervlak
| Definitie De meetkundige plaats van de punten die een gegeven afstand r tot een gegeven punt M hebben, heet een bol. M heet het middelpunt, r de straal van de bol. Notatie: bol(M, r) of bol(M). |
| . |
| Stelling 1 Een vlak heeft met een bol een cirkel, een punt of niets gemeen of Een vlak snijdt een bol volgens een cirkel, raakt een bol in een punt of snijdt een bol niet. |
Klik hier >
< voor een Cabri 3D applet bij deze stelling
(automatische draaiing; opent in een NieuwVenster)
Bewijs:
 |
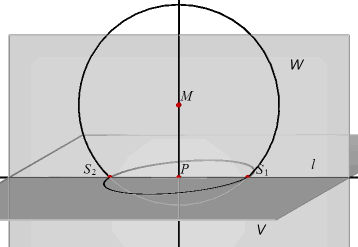Gaat het vlak V door M, dan is de doorsnede van V en de bol de meetkundige plaats van
de punten in V die een afstand r tot M hebben. De doorsnede is dan een cirkel. Gaat het
vlak V niet door M, dan laten we een loodlijn MP neer op V. Een vlak W door MP (dat is een
loodvlak op V) gaat dus door M. De doorsnede van V en de bol is dan dus een cirkel met
straal r. W snijdt V volgens een lijn l. Merk op dat alle doorsneden van bollen met vlakken door MP (cirkels met gelijke straal, r) congruent zijn. |
Hieruit volgt nu voor bovenstaande gevallen:
(1) alle lijnstukken PS1, PS2 zijn bij elk vlak door MP aan elkaar
gelijk. De meetkundige plaats van de snijpunten S1, S2 is dus een
cirkel met middelpunt P en straal (bijv.) PS1;
(2) het vlak V heeft met de bol alleen het punt P gemeenschappelijk;
(3) het vlak V snijdt de bol niet.¨
| Definities (1) De snijcirkel van een bol en een vlak dat door het middelpunt van de bol gaat, heet grote cirkel van de bol. De overige cirkels heten kleine cirkels. (2) Een vlak dat met een bol precies een punt gemeenschappelijk heeft, heet raakvlak aan de bol. Het gemeenschappelijk punt heet raakpunt. |
Uit het bewijs van Stelling 1 volgt direct:
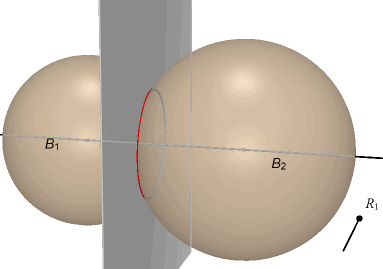
| Stelling 3 Twee bollen snijden elkaar volgens een cirkel, raken elkaar in een punt (er is één gemeenschappelijk punt) of snijden elkaar niet. |
| . |
 |
Klik hier >< voor een Cabri 3D applet van deze figuur
(automatische draaiing; opent in een NieuwVenster). |
Bewijs:
 |
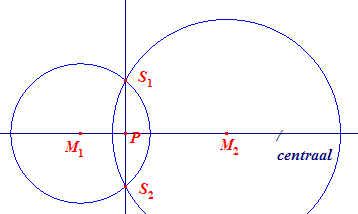We snijden de beide bollen met een willekeurig vlak door de centraal van de bollen (de
centraal is de lijn door de beide middelpunten). Dit vlak snijdt beide bollen volgens een cirkel (stelling 1), resp. met middelpunt M1 en middelpunt M2. Er zijn drie mogelijkheden: (1)...... de cirkels snijden elkaar in twee punten, S1 en S2; (2)...... de cirkels raken elkaar in een punt P (dat op de centraal ligt); (3)...... de cirkels snijden elkaar niet. Merk op dat alle doorsneden van de bollen met vlakken door M1M2 congruent zijn! Hieruit volgt dan voor bovengenoemde gevallen: |
(1) alle lijnstukken PS1 en PS2 zijn gelijk en staan in P
loodrecht op de centraal. Dus is de meetkundige plaats van S1, S2
een cirkel met middelpunt P in het vlak door P loodrecht op de centraal.
(2) de bollen hebben alleen punt P gemeenschappelijk;
(3) de bollen snijden elkaar niet.¨
| Definitie Als twee bollen elkaar raken, dan heet het gemeenschappelijk punt het raakpunt van die bollen. |
Uit het bewijs van stellling 3 volgt nu direct:
| Stelling 4 Het middelpunt van de snijcirkel van twee bollen ligt op de centraal; het snijvlak staat loodrecht op de centraal. Het raakpunt van twee bollen ligt op de centraal. |
Opmerking
Als de beide bollen elkaar raken, dan is het vlak door P loodrecht op de centraal het gemeenschappelijk
raakvlak van de bollen.
Liggen de bollen ter weerszijden van het raakvlak, dan zeggen we dat de bollen elkaar uitwendig
raken. Liggen de bollen aan eenzelfde kant van het raakvlak, dan is er
inwendige raking
Zie ook : Bol, raakvlak, omhullingskegel
[einde Opmerking].
[p : bol.htm] laatste wijziging op: 28-09-2005