Een gelijkzijdige driehoek als invers beeld van drie collinaire punten
Overzicht ][ Inversie | Meetkunde | Cabri
Overzicht - Een toepassing
van hoektrouw bij inversie ![]()
| Stelling 1 Elk drietal collineaire punten kan door een inversie worden afgebeeld op de hoekpunten van een gelijkzijdige driehoek. |
Omdat een inversie I een afbeelding is waarvoor geldt I2 = E (waarbij E de
identieke afbeelding is), bekijken we het probleem eerst maar eens "van de andere
kant".
Wat is er te zeggen van het beeld van de hoekpunten van een gelijkzijdige driehoek
onder een inversie?
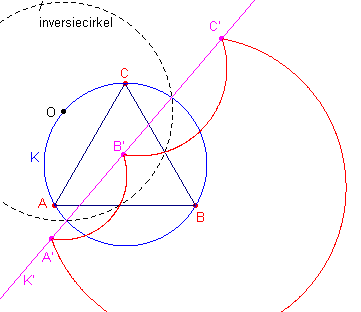 |
[1] Zoals bekend (zie de pagina "Inversie") is het mogelijk een cirkel af te beelden op een rechte lijn. Voorwaarde daarvoor is dat die cirkel door het inversiecentrum gaat. We gaan uit van een gelijkzijdige driehoek ABC. We kiezen een inversie waarbij het centrum O op de omcirkel van ABC ligt. De punten A', B', C' (beelden van A, B, C) liggen nu op de beeldlijn (de rechte lijn K') van de omcirkel K. De zijden van de driehoek worden afgebeeld op cirkelbogen met eindpunten A', B', C'. |
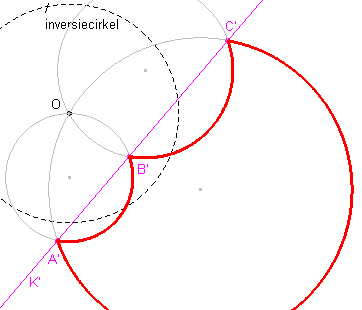 |
[2] We merken op, dat de dragers van de zijden (de lijnen AB, BC en CA) afgebeeld worden op de cirkels die dragers zijn van deze cirkelbogen. Het oneigenlijke punt van elk van de lijnen AB, BC en CA wordt dan afgebeeld op het centrum O van de inversie. Die drie cirkels, de dragers van de cirkelbogen, gaan dus alle door het punt O. |
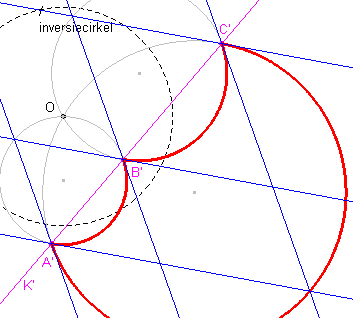 |
[3] Maar er is meer. Wat gebeurt er met de hoeken van driehoek ABC (alle 60º)? Het gevolg van het feit dat inversie een hoektrouwe (conforme) afbeelding is, is nu, dat deze cirkels (cirkelbogen) in hun snijpunten ook hoeken van 60º met elkaar maken. Met andere woorden: De raaklijnen in de snijpunten van de cirkels aan die cirkels maken met elkaar hoeken van 60º. Dat geldt trouwens ook voor de hoek die zo'n raaklijn maakt met de lijn K'! Immers zo'n raaklijn is het beeld van de raaklijn in een hoekpunt van ABC aan de omcirkel van ABC. |
En hiermee hebben we een constructief bewijs van Stelling 1 (zie hiervoor paragraaf 2).
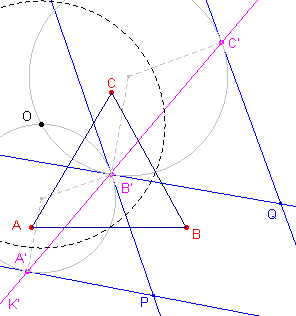 |
We gaan uit van drie collineaire punten A', B', C' (op de lijn K'). Op grond van het bovenstaande (in [2]) is het voldoende twee beeldcirkels (van de zijden van ABC) te construeren. We construeren lijnen A'P en B'P met B'A'P = 60º en A'B'P = 60º en lijnen B'Q en C'Q met C'B'Q = 60º en B'C'Q = 60º. Vervolgens construeren we een cirkel die in A' raakt aan A'P en in B' raakt aan B'P, en een cirkel die in B' raakt aan B'Q en in C' aan C'Q. Het tweede snijpunt van deze cirkels (niet zijnde B') is het centrum O van de inversie. Met een willekeurige inversiemacht (straal van de inversiecirkel) kunnen we nu A', B', C' afbeelden op de hoekpunten A, B, C van een gelijkzijdige driehoek. En hiermee is de hierboven genoemde stelling (Stelling 1) bewezen. ¨
|
| Stelling 2 Als B' tussen A' en C' ligt, geldt voor de punten O, A, B, C: |OB| = |OA| + |OC| ......(1) en |1 / OB'| = |1 / OA'| + |1 / OC'| ......(2) |
Klik hier >![]() < voor een CabriJavapplet
bij Stelling 2.
< voor een CabriJavapplet
bij Stelling 2.
Bewijs:
Uit de eigenschappen van inversie volgt voor de lengte van de lijnstukken AB en A'B'
waarbij A', B' de beelden zijn van A, B bij een inversie met centrum O en inversiemacht r
(straal van de inversiecirkel):
A'B' = (r2 . AB) / (OA . OB)
(zie de pagina "Inversie", paragraaf Inversie en vermenigvuldiging).
We hebben nu, als AB = BC = CA = d:
A'B' = (r2 . d) / (OA . OB) ; B'C'
= (r2 . d) / (OB . OC) ; C'A' = (r2
. d) / (OC . OA)
Ligt B' tussen A' en B' dan geldt dus A'B' + B'C' = A'C', waaruit we vinden:
![]()
of na vermenigvuldiging met OA . OB .
OC en deling door r2:
(1) ...... OB = OC + OA
Analoog vinden we ook:
AB = (r2 . A'B') / (OA' . OB') ;
BC = (r2 . B'C') / (OB' . OC') ;
CA = (r2 . C'A') / (OC' . OA')
of
![]()
waaruit dan volgt:
(2) ...... 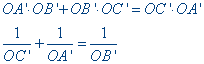
¨
4. Download
![]()
Enkele figuren van deze pagina en de figuren die gebruikt zijn in de CabriJavapplets
kunnen in één bestand via deze website worden gedownload.
Klik hier om het downloaden te starten
(ZIP-bestand; ca. 8kB).