Pool en poollijn (projectief)

Overzicht ][ ProjMeetkunde | Meetkunde

Overzicht

 terug
  1. Inleiding met inversie cabrisignal
  2. Involutie op een kegelsnede cabrisignal
  3. Constructies
  4. Download

1. Inleiding met inversie terug

figuur 1a figuur 1b

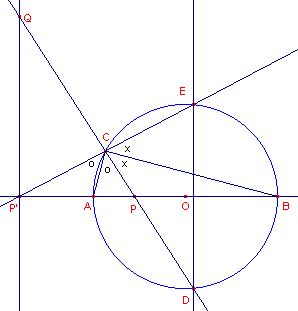
          poollijn1a

     poollijn1b

We kiezen een punt P binnen een cirkel (met straal r) en bepalen de inverse P' van P ten opzichte van deze cirkel (zie figuur 1a).
Dan is
OP x OP' = r2 (definitie van inversie)
Voor de dubbelverhouding op de lijn PP’ die de cirkel in A en B snijdt, hebben we dan:
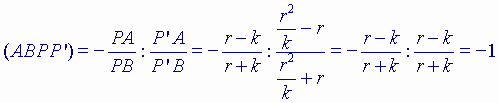
poollijn1for
waar OP = k, zodat OP’ = r2 / k.

We bekijken nu de punten Q van de lijn p die in P’ loodrecht staat op AB.
We zullen aantonen, dat ook P en Q harmonisch (gescheiden) liggen ten opzichte van de punten A en B.

Klik hier Animatie voor een CabriJavapplet waarmee dit kan worden geïllustreerd.

De lijnenbundel met top C geeft nu (op grond van de definitie): C(ABPP’) = -1, waarbij CA _|_ CB (immers C ligt op een Thales-cirkel met middellijn AB).
De lijnen CA en CB zijn dan bissectrices van PCP’ en PCE.
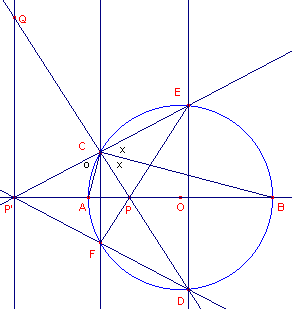
Hieruit volgt dat bg AD = bg AC; dus AB _|_ DE. Zie nu verder figuur 1b.
Op dezelfde manier kunnen we laten zien, dat CF _|_ AB.
Bekijken we nu de volledige vierzijde CEDF. P’ is hiervan een hoekpunt. Het overstaande hoekpunt van P’ is het snijpunt van CF en ED (dit is het oneigenlijke punt van de lijn p).
p is dus diagonaal van de volledige vierzijde.
Volgens de symmetrie in AB gaat de diagonaal EF dus eveneens door het punt P.
En dan hebben we (CDPQ) = -1.
Nu is bewezen:

Stelling 1a
De meetkundige plaats van de punten Q met (ABPQ) = -1 waarbij A en B snijpunten zijn van de lijn door P en Q met een cirkel met middelpunt O is een rechte lijn die loodrecht staat op OP (met P binnen de cirkel).

Vraag

: Wat nu als P buiten de cirkel ligt?
Het bovenstaande bewijs verloopt dan analoog, mits we het punt Q (op p) maar binnen de cirkel kiezen.
Immers, het bewijs is gebaseerd op de snijpunten C en D van de lijn p en de cirkel.
Het geval dat Q buiten de cirkel ligt, laten we op dit moment voor wat het is. We komen daarop terug in paragraaf 2.
Vooruitlopend daarop geven we een definitie.
Definitie
De lijn p heet de poollijn van P ten opzichte van de cirkel.
Het punt P heet de pool van de lijn p ten opzichte van de cirkel.

We kunnen Stelling 1a dus herformuleren als
Stelling 1b
De meetkundige plaats van de punten die met een punt T harmonisch liggen met de snijpunten van een lijn door T en een cirkel, is de poollijn van T ten opzichte van die cirkel.

2. Involutie op een kegelsnede

 terug
figuur 2a 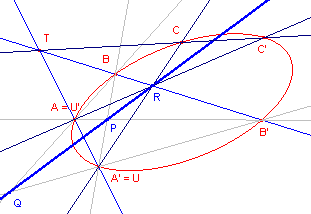poollijn2 We bekijken een lijnenbundel met top T. Deze lijnenbundel laten we een involutie insnijden op een kegelsnede K.
In nevenstaande figuur hebben dan de paren A, A’ en B, B’. We kunnen het paar A, A’ ook opvatten als opvolgend U’, U.
De snijpunten AB’ /\ A’B = P en B’U /\ BU’ = Q bepalen nu de Pascal-lijn p van de zeshoek AB’UA’BU’ (een en ander volgens de Stelling van Pascal).

Voor een willekeurig punt C van K (met toegevoegd punt C’) geldt dan:
AC’ /\ A’C (= R) ligt eveneens op de betreffende Pascal-lijn.

Gevolg


Als de punten C en C’ op K samenvallen, dan is de lijn TC uit de bundel de raaklijn uit T aan K.
[einde Gevolg]

Klik hier Animatie voor een CabriJavapplet ter illustratie.

We bewijzen nu:
Stelling 2
De lijn p is de meetkundige plaats van het 4e harmonische punt op de straal door T ten opzichte van de snijpunten van die straal met K.

Bewijs:
figuur 2b 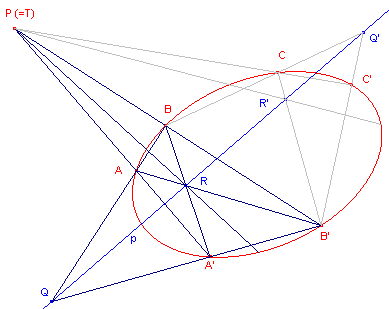poollijn2b Q en R zijn de diagonaalpunten van de volledige vierhoek AA’B’B.
Q’ en R’ zijn de diagonaalpunten van de volledige vierhoek BCC’B’.

De lijn p is dus (conform de eigenschappen van de volledige vierhoek) de meetkundige plaats van de 2e en 3e diagonaalpunten wier 1e diagonaalpunt het punt P is.

Of ook:

p

 is de meetkundige plaats van de 4e harmonische met stralen door P tov. de snijpunten van die straal met de kegelsnede. ¨

We noemen de lijn p de poollijn van P ten opzichte van de parabool. Het punt P heet ook nu de pool van het punt P.

Klik hier Animatie voor een CabriJavapplet waarin dit wordt geïllustreerd.

figuur 2c 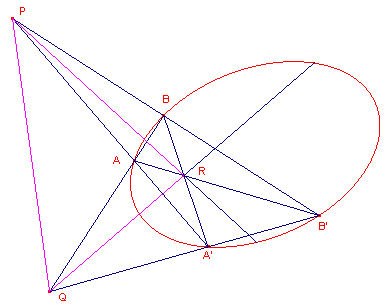poollijn2c Gevolgen
[1]
PR is de poollijn van Q en QP is de poollijn van R (zie figuur 2c).
[2]
Indien een punt op de kegelsnede ligt, dan is de raaklijn in dat punt tevens poollijn van dat punt tov. de kegelsnede.
[einde Gevolgen]

Driehoek PQR wordt een pooldriehoek van de kegelsnede genoemd.
.
Stelling 3
De poollijnen van de punten van p gaan door P
of
Als Q op de poollijn van P ligt, dan ligt P op de poollijn van Q.

Bewijs:
figuur 3 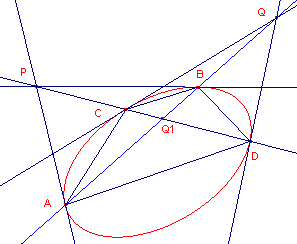poollijn3 Zij Q een punt van p. Op deze lijn ligt dan het punt Q1 zodat (ABQQ1) = -1.
De lijn PQ1 snijdt de kegelsnede in C en D.
De volledige vierhoek ACBD is nu ingeschreven in de kegelsnede. P, Q en Q1 zijn daarvan de diagonaalpunten (de hoekpunten van een pooldriehoek). ¨

3. Constructies terug
We kunnen nu eenvoudig de poollijn van een punt, de pool van een lijn en raaklijnen aan een gegeven kegelsneden construeren.

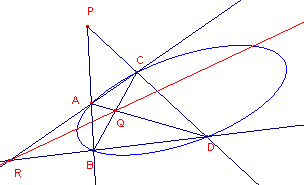poollijn4a		 Poollijn van een punt P

Teken door P twee lijnen die de kegelsnede snijden in opvolgend de punten A,B en C,D.
Deze vier punten bepalen een volledige vierhoek. Het tweede en derde hoekpunt (Q en R) van de pooldriehoek bij P bepalen dan de poollijn van P.
  

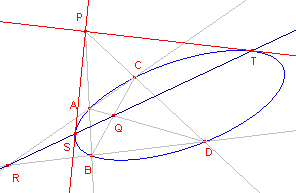poollijn4b		 Raaklijnen uit P

De poollijn van P snijdt de kegelsnede in S en T.
De lijnen PS en PT zijn de raaklijnen.
  

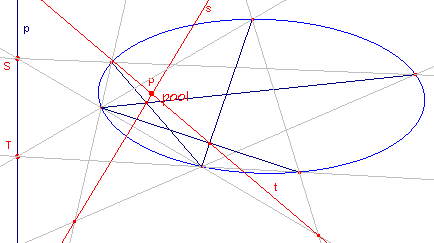poollijn4c		 Pool van een lijn p

Kies op de lijn twee punten (S en T) en bepaal van elk van deze twee punten de poollijn tov. de kegelsnede (s en t).
Het snijpunt P van de beide poollijnen is de gevraagde pool.
  

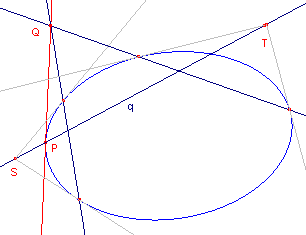poollijn4d		 Raaklijn in een punt P

Kies op een willekeurige lijn q door P twee punten S en T en bepaal van deze punten de poollijnen tov. de kegelsnede. Verbind het snijpunt Q van deze lijnen met het punt P. PQ is de gevraagde raaklijn.
.
Stelling 4
Een ingeschreven vierhoek en de bijbehorende omgeschreven vierzijde hebben dezelfde pooldriehoek ten opzichte van een kegelsnede.

Bewijs:
figuur 5 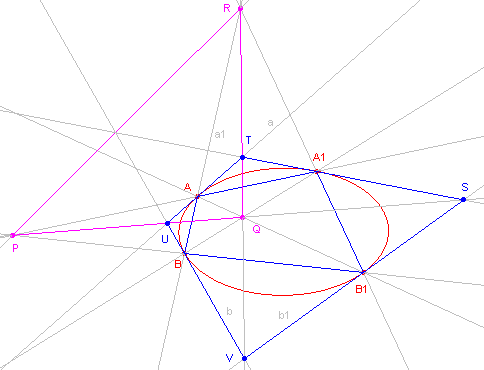poollijn5 Zie figuur 5.

De lijnen AB, A1B1 gaan door R. De polen van deze lijnen moeten dus op de poollijn van R liggen.
Deze polen zijn de raaklijnen a, b en a

1, b1.
De poollijn van R is PQ.
De bedoelde raaklijnen snijden elkaar dus op PQ (in U, en in S).
Op dezelfde manier kunnen we beredeneren, dat a, a1 en b, b1 elkaar snijden op QR (in T en in V); en ook dat a, b1 en a1, b elkaar snijden op PR (deze snijpunten zijn niet van een naam voorzien).
Waaruit het gestelde volgt. ¨

4. Download terug
De Cabri-figuren op deze pagina en de figuren van de CabriJavapplets kunnen in éen bestand via deze website worden gedownload.
Klik hier om het downloaden te starten (ZIP-bestand; ca. 11kB).

begin pagina

[poollijn.htm] laatste wijzigig op: 18-01-18