Complex bewijzen - 3

Overzicht  ][  Complexe vlak | Meetkunde

---

Overzicht van deze pagina

Naar pagina 1 | Naar pagina 2

7. Middelloodlijnen van een driehoek
8. Stelling van Napoleon
9. Stelling(en) van Clifford

Naar pagina 4 | Naar pagina 5

7. Middelloodlijnen van een driehoek

Stelling 6 De middelloodlijnen van de zijden van een driehoek gaan door één punt.

Bewijs:
Zijn A, B, C de hoekpunten, met a,b,c de bijbehorende affixen.
Voor de middelloodlijn van BC hebben we de vergelijking (zie paragraaf 6.2):
Det[ [x, x_, 1], [b, c_, 1], [c, b_, 1] ] = 0.
Uitgewerkt geeft dit:
(c_ - b_)x + (c - b)x_ + (bb_ - cc_) = 0
(b_ - c_)x + (b - c)x_ = |b|² - |c|² ...... (1)

Analoog vinden we voor:
middelloodlijn CA: (c_ - a_)x + (c - a)x_ = |c|² - |a|² ......(2)
middelloodlijn AB: (a_ - b_)x + (a - b)x_ = |a|² - |b|² ......(3)
Wanneer we deze uitdrukkingen bij elkaar optellen, krijgen we een uitdrukking die equivalent is met de uitdrukking voor de middelloodlijn van BC.
Dit betekent dat een oplossing x die aan (2) en aan (3) voldoet, de affix van het snijpunt van beide, ook voldoet aan (1).¨

8. Stelling van Napoleon

Lemma 1 Een gelijkzijdige driehoek abc is gelijkvormig met 1ww2 of met 1w2w.

Bewijs:
Voor een gelijkzijdige driehoek abc geldt (bijvoorbeeld): abc ~ cab.
Dus Det[ [a, c, 1], [b, a, 1], [c, b, 1] ] = 0.
Uitgewerkt:
a² - bc - ab + c² + b² - ac = 0
en ontbonden (met w² + w + 1 = 0):
(a + wb + w²c)(a + w²b + wc) = 0
waaruit ook
Det[ [a, 1, 1], [b, w, 1], [c, w², 1] ] = 0 (klokrichting) OF
Det[ [a, 1, 1], [b, w², 1], [c, w, 1] ] = 0 (tegenklokrichting).¨

Stelling 7 (Napoleon) Zijn op de zijden van een willekeurige driehoek A1A2A3 buitenwaarts gelijkzijdige BiAjAk driehoeken geconstrueerd, dan vormen de zwaartepunten Zi van die driehoeken eveneens een gelijkzijdige driehoek (de Napoleon-driehoek van A1A2A3).

Zie ook het Cabri-werkblad "Het punt van Fermat en de driehoek van Napoleon".

Bewijs:

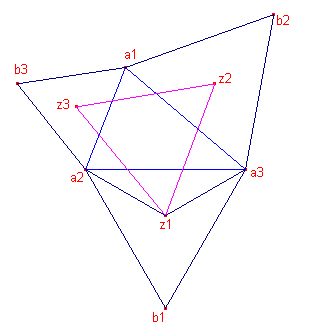We gaan ervan uit dat alle buitenwaarts getekende driehoeken klok-georiënteerd zijn. Voor z1a3a2 geldt dan: z1a3a2 ~ 01w. Dus: 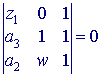. Uitgewerkt: z1(1 - w) +a3w - a2 = 0 of z1 = (a2 - a3w) / (1 - w) Evenzo vinden we: z2 = (a3 - a1w) / (1 - w) z3 = (a1 - a2w) / (1 - w) We onderzoeken nu of z1z2z3 gelijkzijdig is. We berekenen z1 + z2w + z3w2 (zie bovenstaand Lemma).

z₁ + z₂w + z₃w² =
     = (a₂ - a₃w + a₃w - a₁w² + a₁w² - a₂w³) / (1 - w)
     = 0
Waarmee is aangetoond, dat de driehoek z₁z₂z₃ inderdaad gelijkzijdig is.¨

9. Stelling(en) van Clifford

Lemma 2 Zijn Ci (i=1, ...,4) cirkels. Cirkel Ci snijdt cirkel Ci+1 in zi en wi . De punten zi zijn conclyclisch (cirkel Z) DESDA de punten wi zijn concyclisch (cirkel W).

Opmerking
Conclyclisch houdt ook in "collineair"; de cirkel gaat dan door z = ¥ (oneindig; zie Afbeeldingen - 3).
[einde Opmerking]

Bewijs:

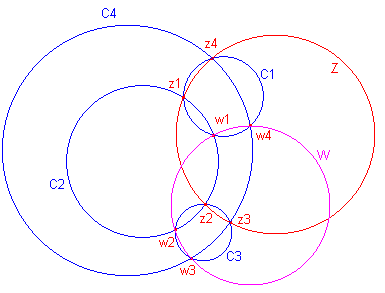We hebben (volgend uit de gegevens):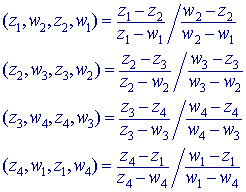 Bovenstaande uitdrukking zijn alle reëel (zie Stelling 3 op pagina 1). We kunnen hieruit afleiden:

 
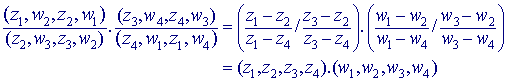
Het meest linker lid van deze uitdrukking is reëel.
Dus (z₁,z₂,z₃,z₄) is reëel desa (w₁,w₂,w₃,w₄) is reëel.¨

Definitie (Zie de figuur hiernaast) De punten P1, P2, P3 heten Clifford-punten van het stelsel cirkels {C1, C2, C3}. De cirkel door P1, P2, P3 heet de Clifford-cirkel van {C1, C2, C3}. Een Clifford-stelsel bestaat uit n cirkels (n > 2) die precies één punt, ic. het punt P, gemeenschappelijk hebben. Opmerking Het punt P mag samenvallen met het punt z = ¥ (oneindig). Het Clifford-stelsel bestaat dan uit n rechte lijnen (in "algemene ligging"). [einde Opmerking]

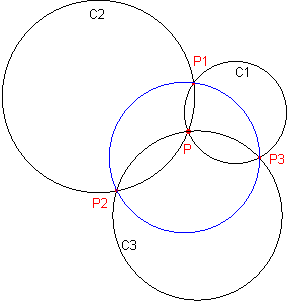
Stelling 8 (Clifford) Gegeven is een Clifford-stelsel Ci (i = 1,2,3,4) door een punt P (zie figuren hieronder). Pi j is het (tweede) snijpunt van Ci en Cj. Ci j k is de Cifford-cirkel van Pi jPj kPi k. Dan gaan de vier Clifford-cirkels van {Ci} door een tweede punt P1234.

Bewijs:

P eindig		P = ¥

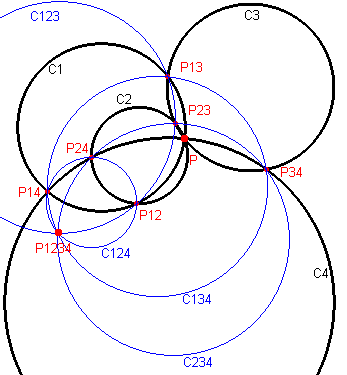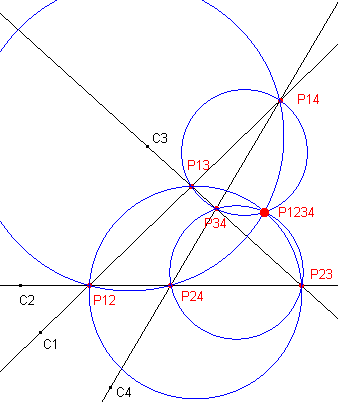Klik hier voor een CabriJavapplet bij de linker figuur.
Klik hier voor een CabriJavapplet bij de rechter figuur.

In het onderstaande betekent X&Y: het snijpunt (de snijpunten) van lijn X en lijn Y.
We bekijken de cirkels C1, C2, C134, C234.
C1&C2 = {P, P12}; C1&C134 = {P13, P14}; C2&C234 = {P23, P24}; C134&C234 = {P34, P1234}.
Hierbij is P1234 het tweede snijpunt van beide laatst genoemde cirkels.
De punten P, P13, P23, P34 zijn concyclisch (alle op C3).
Volgens Lemma 2 zijn dan ook de punten P12, P14, P24 en P1234 concyclisch.
C124 is de omcirkel van P12P14P24.
P1234 ligt dus ook op C124.
Maar ook: P, P14, P24, P34 zijn concyclisch (alle op C4).
De punten P12, P13, P23, P1234 zijn dus (weer volgens Lemma 2) concyclisch.
C123 is de omcirkel van P12P23P13.
P1234 ligt dus ook op C123.
De cirkels C123, C124, C134 en C234 gaan dus alle door P1234.¨

Van vier naar vijf
Bij een Clifford-stelsel bestaande uit vier cirkels hebben we dus één Clifford-punt (zie Stelling 8) .
Kiezen we een stelsel van vijf cirkels, dan leveren telkens vier hiervan een Clifford-punt:
P1234, P1235, P1245, P1345, P2345.

Stelling 9 Bij een Clifford-stelsel met n = 5 liggen de daarbij behorende vijf Clifford-punten op een cirkel (de Clifford-cirkel voor n = 5).

Bewijs:

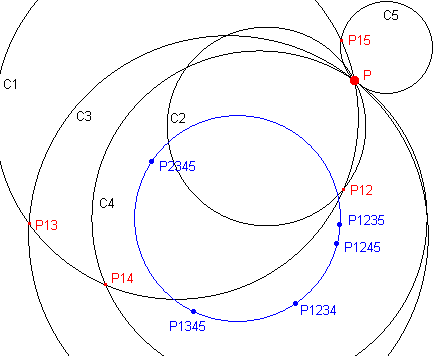We bewijzen, dat P1234, P1235, P1245, P1345 concyclisch zijn. P1234 = C124&C134 P1235 = C123&C125 P1245 = C145&C125 P1345 = C134&C135 Deze cirkels hebben opvolgend als tweede snijpunt: P14, P12, P15, P13. Deze punten zijn concyclisch (ze liggen immers op C1). Volgens Lemma 2 zijn dus P1234, P1235, P1245, P1345 eveneens concyclisch. Analoog kunnen we aantonen, dat ook P2345 op deze cirkel (te weten C12345) ligt.¨

Van vijf naar zes
Als we bij een Clifford-stelsel met n = 6 telkens vijf lijnen kiezen, dan leveren deze zes Clifford-cirkels.

Stelling 10 Bij een Clifford-stelsel met n = 6 gaan de zes Clifford-cirkels door één punt.

Bewijs:

[wordt voortgezet]

---

¤ Klik hier voor de volgende pagina

[bewijs3.htm] laatste wijziging op: 09-06-02