Complex bewijzen - 2

Overzicht  ][  Complexe vlak | Meetkunde

Overzicht van deze pagina terug

Naar pagina 1

  1. Gelijkvormige driehoeken
  2. Drie punten op een lijn
  3. Vergelijking van een lijn
       6.1. Lijn door twee punten
       6.2. Middelloodlijn van een lijnstuk
       6.3. Loodlijn op een lijn
       6.4. Stelling van Thales
       6.5. Een lijn door twee punten van de eenheidscirkel

Naar pagina 3 | Naar pagina 4 | Naar pagina 5

4. Gelijkvormige driehoeken terug

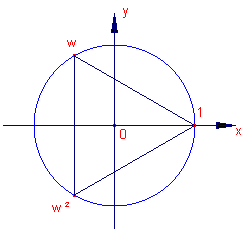bewijs21 Allereerst bekijken we de oplossingen van de vergelijking: z3 = 1.
De oplossingen kunnen we terugvinden op de eenheidscirkel, als de hoekpunten van een gelijkzijdige driehoek.
Deze oplossingen geven we aan met 1, w, w2.
Hierbij geldt:
w2 = w_ en w2 + w + 1 = 0
We zullen van deze bijzondere getallen een enkele keer gebruik maken.
Zie ook de pagina "Afbeeldingen van het complexe vlak - 2, paragraaf 3. Voorbeelden.

We maken onderscheid tussen directe en indirecte gelijkvormigheid.
We schrijven
directe gelijkvormigheid:    abc ~ pqr
indirecte gelijkvormigheid: abc ~ pqr (r)
Bij directe gelijkvormigheid hebben de hoeken dus alle eenzelfde oriëntatie (alle kloks of alle tegenkloks).

Stelling 4a
abc ~ pqr DESDA 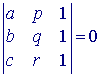bewijs22

Bewijs:
Bij gelijkvormige driehoeken is het voldoende, dat twee paar overeenkomstige zijden dezelfde verhouding hebben, en dat de hoek ertussen gelijk is.
Dus: 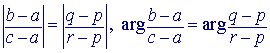bewijs23
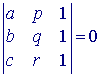Hieruit volgt onmiddellijk, dat bewijs24, hetgeen equivalent is met bewijs22. ¨

Gevolg:

Stelling 4b
abc ~ pqr (r) DESDA 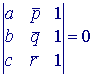bewijs25

Bewijs:
abc ~ p_q_r_, waaruit het gestelde volgt (via Stelling 4a). ¨

5. Drie punten op een lijn terug

Stelling 5
Drie punten A, B, C met affixen a,b,c liggen op een lijn, indien 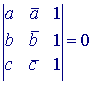bewijs26.

Bewijs:
Nu geldt: abc ~ a_b_c_, waaruit het gestelde volgt (via Stelling 4a). ¨

6. Vergelijking van een lijn terug

6.1. Lijn door twee punten terug
Zijn A en B de beide punten, met affixen a en b.
Het willekeurige punt X, met affix x, ligt op AB indien (zie Stelling 5): bewijs27
Dit is dus de vergelijking van de lijn.
Uitgewerkt:
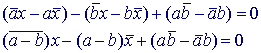
bewijs28

6.2. Middelloodlijn van een lijnstuk terug

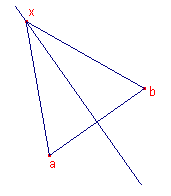bewijs29 Is AB het lijnstuk (affixen a en b), dan geldt: xab ~ xba (r).
De vergelijking van de lijn is dan (volgens Stelling 4b):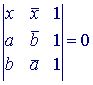bewijs2a.

6.3. Loodlijn op een lijn terug
Zij p = x + iy, dan is p_ = x - iy.
Voor (ip)_ geldt dan (ip)_ = (-y + ix)_ = -y - ix = -i(x - iy) = -i.p_.

De lijn door de punten A en B (affixen a en b) is evenwijdig aan a - b.
De loodlijn op AB is dan dus evenwijdig i(a - b).
In de vergelijking van de lijn AB (zie 6.1): (a - b)_x - (a - b)x_ + c = 0 kunnen we dus (a - b) vervangen door i(a - b) om een loodlijn op AB te krijgen.

De loodlijn door p op AB heeft dan de vergelijking:
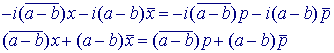
bewijs2b

6.4. Stelling van Thales terug
We kiezen A met affix 1 en B met affix -1; AB is dus de middellijn van de eenheidscirkel.
Voor PA _|_ PB geldt dan (p - 1) _|_ (p + 1).
Dan is (p - 1)/(p + 1) imaginair, zodat
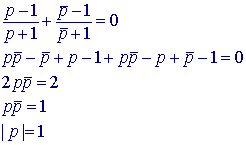
bewijs2c
Dus P ligt eveneens op de eenheidscirkel.

6.5. Een lijn door twee punten van de eenheidscirkel terug
Zijn a en b twee punten op de eenheidscirkel.
Voor AB hebben we dan (zie 6.1):
(a_ - b_)x - (a - b)x_ + (ab_ - a_b) = 0.
Nu is: a_ = 1/a en b_ = 1/b, zodat:
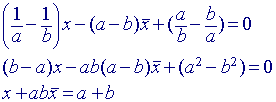
bewijs2d

¤ Klik hier voor de volgende pagina
begin pagina

[bewijs2.htm] laatste wijziging op: 03-03-02