Meetkundige plaats op een rooster (met CabriPlus)
[ CabriPlus | Cabri | Meetkunde ]
We gaan uit van een willekeurig roosterpunt P en een basisdriehoek ABC.
We bepalen van het punt P de voetpuntsdriehoek A'B'C' tov.
driehoek ABC.
| figuur 1 |  |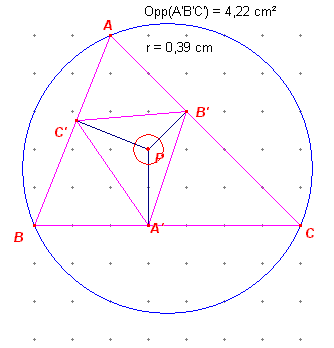
De hoekpunten A, B, C zijn eveneens roosterpunten. Van driehoek ABC
is ook de omcirkel getekend. Ten einde de oppervlakte van de voetpuntsdriehoek te onderzoeken, tekenen we om het punt P een cirkel, waarvan de oppervlakte evenredig is met de oppervlakte van de voetpuntsdriehoek. |
| figuur 2 |  |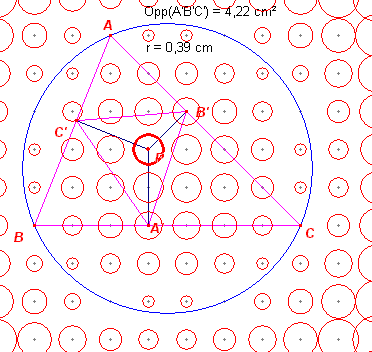
In deze figuur is de meetkundige plaats getekend van het cirkeltje rondom
P, als P het rooster doorloopt. We merken op, dat de straal van deze cirkeltje kleiner wordt naar mate de roosterpunten dichter bij de omcirkel liggen (zie ook figuur 3). |
| figuur 3 |  |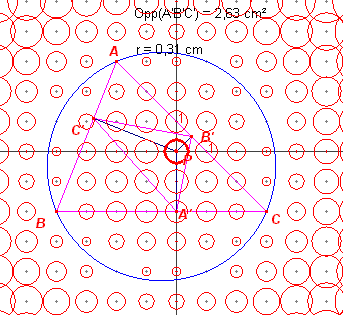
In deze figuur is de grootte van de eenheid op de assen gewijzigd. Dit illustreert hetgeen gevonden is bij figuur 2, wellicht iets beter. |
[cabrimp.htm] laatste wijziging op: 29-04-03