Affiene afbeeldingen van het vlak op zichzelf

Overzicht  ][  Proj.Meetkunde | Meetkunde

0. Overzicht terug

  1. Inleiding cabrisignal
  2. Enkele eigenschappen
  3. Voorbeelden van affiene afbeeldingen
       3.0. "Euclidische" afbeeldingen
       3.1. Scheve lijnspiegeling cabrisignal
       3.2. Scheve lijnvermenigvuldiging cabrisignal
       3.3. Hyperbolische rotatie cabrisignal
  4. Constructies
       4.1. Coördinatentransformatie
       4.2. Product van "eenvoudige" affiene afbeeldingen cabrisignal
  5. Oppervlakte
  6. Referenties
      
  7. Download

1. Inleiding terug
We bekijken afbeeldingen van het vlak opzichzelf, waarbij collineariteit en evenwijdigheid invariant zijn. Dergelijke afbeeldingen heten affiene afbeeldingen. We geven de volgende "eenvoudige" definitie.

Definitie
Een affiene afbeelding is een 1-1-afbeelding (van het vlak op zichzelf) die elk 3-tal collineaire punten afbeeldt op collineaire punten.
.
Stelling 1
De affiene beelden van 3 niet-collineaire punten zijn niet-collineair.

Bewijs:

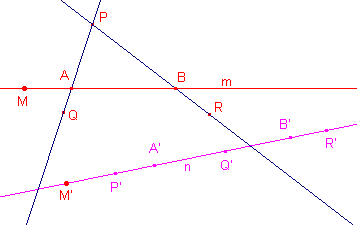affien1 We bewijzen uit het ongerijmde.
(Aanname:) Stel de punten P, Q, R hebben collinaire beelden P', Q', R' (op de lijn n).
Zij M een willekeurig punt. Zij m een willekeurige lijn door M (niet zijnde MP) die de lijnen QP en RP snijdt in opvolgend A en B.
P, Q, A zijn collineair, zodat ook P', Q', A' collineair zijn (volgens de definitie). A' ligt dus op n.
Evenzo ligt dan ook B' op n.
M, A, B zijn collineair, zodat M', A', B' collineair zijn. M' ligt dus op n.
Omdat M willkeurig is, wordt dus het gehele vlak afgebeeld op de lijn n. De afbeelding is dus niet 1-1. Tegenspraak!
De punten P', Q', R' zijn dus niet-collineair. ¨
Gevolgen
- De inverse van een affiene afbeelding is affien.
- Het beeld van een rechte lijn onder een affiene afbeelding is een rechte lijn
.
Stelling 2
De affiene beelden van twee evenwijdige (niet-samenvallende) lijnen zijn evenwijdig.

Bewijs:

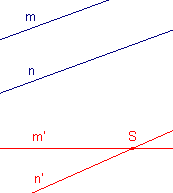affien2 (Aanname:) Stel de beelden m' en n' van m en n (m // n) snijden elkaar in het punt S.
Het origineel So van S ligt nu op m; maar ook: het origineel So van S ligt op n.
De lijnen m en n hebben het punt So gemeen. Tegenspraak!  ¨
Gevolg
Het affiene beeld van het snijpunt van twee lijnen is het snijpunt van de affiene beelden van de lijnen.
Stelling 3
Het affiene beeld van het midden van een lijnstuk is het midden van het beeldlijnstuk.

Bewijs:

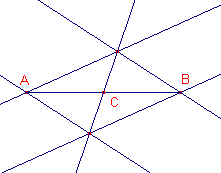affien3 Zij C het midden van het lijnstuk AB
Teken twee lijnen door A (niet zijnde de drager van AB) en teken twee lijn door B evenwijdig met die twee lijnen. De vier lijnen vormen dan een parallellogram, waarvan de diagonalen elkaar snijden in C.
Onder een affiene afbeelding is het beeld van dit parallellogram weer een parallellogram (zie Stelling 2). Het beeld C' van C is dan het snijpunt van de diagonalen daarvan.
C' is dus het midden van A'B'. ¨
Gevolg
Delen de punten D1, D2, ..., Dn-1 een lijnstuk AB in n gelijke delen, dan delen hun beelden D1', D2', ..., Dn-1' onder een affiene afbeelding het lijnstuk A'B' eveneens in gelijke delen.

Bewijs:
We hebben: AD = D1D2 = ... = Dn-1B. Dus D1 is het midden van AD2, zodat D1' het midden is van A'D2'.
Enzovoorts.  ¨

Zonder bewijs (maar zie evt. de Opmerking in paragraaf 3.1) vermelden we:

Stelling 4
Zijn A, B, C niet-collineaire punten en zijn A', B', C' eveneens niet-collineaire punten, dan is er precies één affiene afbeelding die A, B, C afbeeldt op A', B', C'.

Klik hier Animatie voor een CabriJavapplet die Stelling 4 illustreert.

De identieke afbeelding is de afbeelding die elk punt van een vlak op zichzelf afbeeldt. We hebben dan:

Gevolg
Als onder een affiene afbeelding drie niet-collineaire punten op zichzelf worden afgebeeld, dan is die afbeelding de identieke afbeelding van het vlak.

Bewijs:
De affiene afbeelding heeft hetzelfde effect als de identieke afbeelding op de drie niet-collineaire punten.
Volgens Stelling 4 is er slechts één dergelijke afbeelding. ¨

2. Enkele eigenschappen terug

Stelling 5
Worden twee verschillende punten van een lijn op zichzelf afgebeeld, dan wordt elk punt van die lijn op zichzelf afgebeeld.

Bewijs:

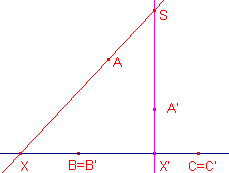affien4 Zijn B = B' en C = C' twee punten van een rechte lijn; zij X een willekeurig punt van die lijn.
Per definitie ligt nu X' op de lijn B'C' (= BC).
Stel X' is verschillend van X.
Zijn verder A en A' twee toegevoegde punten bij de affiene afbeelding.
De lijn AX wordt dan afgebeeld op de lijn A'X'. Het snijpunt S wordt dan onder deze affiene afbeelding afgebeeld op zichzelf. De afbeelding is dan volgens het Gevolg van Stelling 4 de identieke afbeelding.
Maar dan moet gelden: X = X'. Tegenspraak!
Het punt X wordt dus (bij elke affiene afbeelding; immers A en A' zijn willekeurig) op zichzelf afgebeeld. ¨

Opmerking
Een dergelijke lijn wordt wel de affiniteitsas van de affiene afbeelding genoemd. Een affiene afbeelding met een affiniteitsas heet ook wel affiniteit.
[einde Opmerking]

Stelling 6
Als het punt C een lijnstuk AB verdeelt in de verhouding p:q, dan verdeelt ook C' het lijnstuk A'B' in de verhouding p:q, waarbij A', B', C' de beelden zijn van A, B, C bij een affiene afbeelding.
Met andere woorden:.
Bij een affiene afbeelding zijn de verhoudingen op een lijnstuk invariant.

Bewijs:
Is p:q rationaal, dan volgt een en ander uit het Gevolg van Stelling 3.

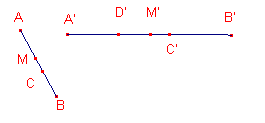affien5 Zij nu p:q irrationaal.
(Aanname:) Stel nu dat affienf1.
We kunnen nu het punt D' op A'B' kiezen, zodat affienf2.

D' valt nu zeker niet samen met C'. We kunnen nu tussen D' en C' een punt M' kiezen, waarvoor de "deelverhouding" rationaal is.
Omdat nu affienf3, ligt C' tussen D' en B', waaruit volgt dat C' ook ligt tussen M' en B'.
Dus ligt C tussen M en B, waarbij: affienf4. Tegenspraak!
Op dezelfde manier kunnen we aantonen, dat ook affienf5 tot een tegenspraak leidt. ¨

3. Voorbeelden van affiene afbeeldingen terug

3.0. "Euclidische" afbeeldingen terug
De zogenoemde orthogonale afbeeldingen, puntspiegeling, lijnspiegeling, rotatie, translatie, zijn affiene afbeeldingen.
Ook de gelijkvormigheidstransformaties, zoals homothetie (vermenigvuldiging), draaivermenigvuldiging, zijn affien.

3.1. Scheve lijnspiegeling terug

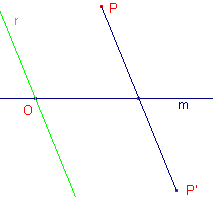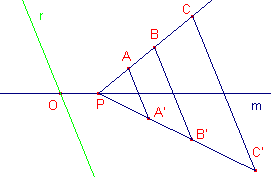
affienv1 Zijn m en r twee lijnen in het vlak.
Het beeld P' van P wordt bepaald via een lijn evenwijdig met r, zodat de lijnstukken die P en P' met het snijpunt op m verbinden, gelijke lengte hebben..

Zie ook de pagina "Generalisatie van de spiegeling".

Opmerking
Als r _|_ m hebben we de "gebruikelijke" (lijn)spiegeling in de lijn m.
[einde Opmerking]

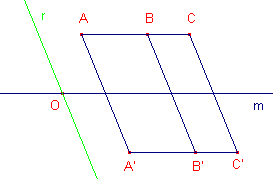
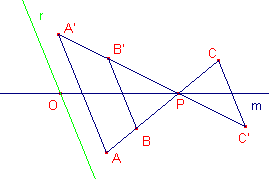
Mogelijke collineaties van drie punten staan in de volgende figuren.

affienv2a affienv2b affienv2c

Opmerking
Eenvoudig is in te zien dat bij de scheve lijnspiegeling hoeken en lengtes van lijnstukken in het algemeen niet invariant zijn.
[einde Opmerking]

Klik hier Animatie voor een CabriJavapplet met een scheve lijnspiegeling van een driehoek.

Stelling 7
Bij een scheve lijnspiegeling is de oppervlakte van een figuur invariant.

Voor het bewijs wordt verwezen naar de pagina "Generalisatie van de spiegeling". ¨

Stelling 8
Het beeld van een cirkel bij een scheve lijnspiegeling is een ellips.

Voor het bewijs hiervan zie de pagina "Generalisatie van de spiegeling". ¨
cabrisignal Op die pagina staat ook een CabriJavapplet.

3.2. Scheve lijnvermenigvuldiging terug

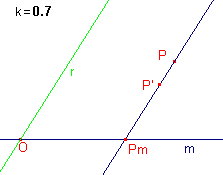affienv3 Uitgaande van een lijn m (de affiniteitsas) en een richting r definiëren we een afbeelding die aan een punt P het punt P' toevoegt met
-  PP' // r
-  PP' /\ m = Pm
-  |PmP'| = k . |PmP| waarbij k > 0
k heet (vermenigvuldigings)factor van de lijnvermenigvuldiging.

Opmerkingen
[1]
Ook voor negatieve vermenigvuldigingsfactor spreken we van een scheve lijnvermenigvuldiging: de afbeelding met factor -k is het product van (ongeacht de volgorde) een lijnvermenigvuldiging met factor k en een lijnspiegeling in m met richting r.
[2]
Staat r loodrecht op m, dan spreken we van een rechte lijnvermenigvuldiging. Vaak wordt dan het woord "rechte" weggelaten.
[einde Opmerkingen]

Klik hier Animatie voor een CabriJavapplet met een scheve lijnvermenigvuldiging van een driehoek.

Stelling 9
Een scheve lijnvermenigvuldiging kan worden vastgelegd door de affiniteitsas en een paar toegevoegde punten (punt en daarmee verschillend beeldpunt).

Bewijs:

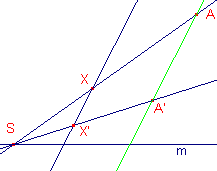affien6 Zij A en A' de toegevoegde punten en m een rechte lijn (de affiniteitsas)
De richting r is gelijk aan de richting van AA'. De factor is gelijk aan SA'/SA, waarbij S = AA' /\ m.
Het beeld van een punt P wordt als volgt bepaald:
- AP /\ m = S
- P' = SA' /\ r
De juistheid van de constructie volgt direct uit de gelijkvormigheid van de van de driehoeken gevormd door de lijnen m en SA' en SA. ¨

3.3. Hyperbolische rotatie terug

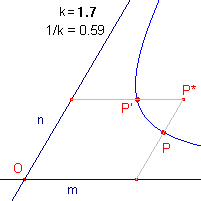
affien7 We gaan uit twee snijdende lijnen m en n.
Het beeld P' van een punt P wordt verkregen door scheve lijnvermenigvuldiging met factor k op m (en richting n) gevolgd door een scheve lijnvermenigvuldiging met factor 1/k op n (met richting m).
Stelling 10
Ligt P op een hyperbool met m en n als asymptoten, dan ligt het beeldpunt P' bij een hyperbolische rotatie met factor k ook op die hyperbool.

Bewijs:
We kiezen de lijnen m en n als assen van een schreef assenstelsel. Zij nu P(x, y) en de hyperbool xy = C.
Dan is P*(x, ky) en P'(1/k . x, y)

Voor de coordinaten x' = 1/k . x en y' = y van het punt P' geldt dus x'y' = xy = C. ¨

Opmerking
Hiermee is de naamgeving van de afbeelding verklaard. Een hyperbool met m en n als asymptoten is invariant onder een hyperbolische rotatie.
[einde Opmerking]

Klik hier Animatie voor een CabriJavapplet met een hyperbolische rotatie van een driehoek.

Stelling 11
Bij een hyperbolische rotatie is de oppervlakte van een figuur invariant.

Bewijs:

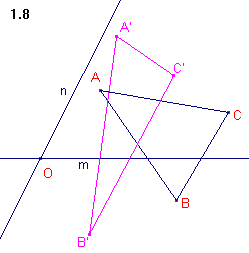affien8 Bij de eerste lijnvermenigvuldiging wordt de oppervlakte vermenigvuldigd met k (de "horizontale" component blijft hetzelfde). Zie het bewijs van Stelling 10.
Bij de tweede lijnvermenigvuldiging wordt de "horizontale" component met 1/k vermenigvuldigd (de "verticale" is nu ongewijzigd).
De oppervlakte wordt dus uiteindelijk vermenigvuldigd met 1/k . k = 1. ¨

Klik hier Animatie voor een CabriJavapplet ter illustratie.

4. Constructies terug
4.1. Coördinatentransformatie terug

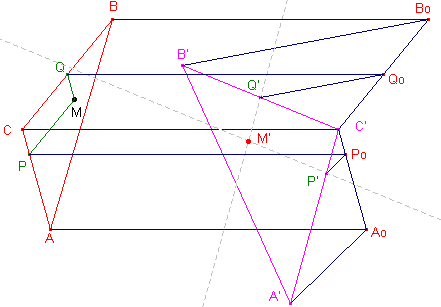affienc1 We beschouwen de lijnen CA en CB als assen van een coördinatenstelsel met C als oorsprong.
We brengen nu de coördinaten van M (een willekeurig punt) tov. dit stelsel over naar een coördinatenstelsel met assen C'A' en C'B' met C' als oorsprong. Dit geeft dan het beeld M' van M.
CC' bepaalt de richting van de transformatie.
Po onstaat uit P, Ao onstaat uit A. De lijn door Po // A'Ao bepaalt P'.
Qo ontstaat uit Q, Bo ontstaat uit B. De lijn door Qo // B'Bo bepaalt Q'
De lijnen door P' // B'C' en door Q' // A'C' bepalen nu het punt M'.

Nu is:
CP : CA = C'Po : C'Ao = C'P : C'A'
En
CQ : CB = C'Qo : C'Bo = C'Q' : C'B' ¨

Opmerking
Met deze "coördinatentransformatie" kan Stelling 4 constructief bewezen worden.
[einde Opmerking]

4.2. Product van "eenvoudige" affiene afbeeldingen terug

Stelling 12
Elke affiene afbeelding is het product van een gelijkvormigheidstransformatie en een affiniteit.

Bewijs:
Zijn A, B, C drie niet-collineaire punten en A', B', C' hun beeldpunten bij een affiene afbeelding T.

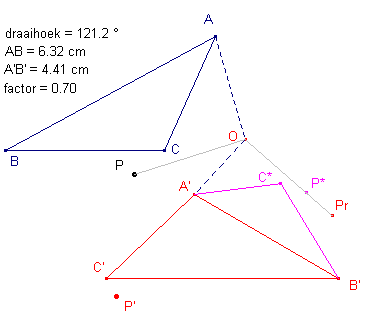affienc2 Zij nu C* het punt waarvoor ABC ~ A'B'C*. De afbeelding die A', B', C* toevoegt aan A, B, C is een affiene afbeelding (directe gelijkvormigheid, via een draaivermenigvuldiging, met centrum O).
Vervolgens bekijken we de affiniteit, die C' toevoegt aan C*, met affiniteitsas A'B'.
Het product S van beide affiene afbeeldingen is weer affien.
Nu is T = S volgens Stelling 4. ¨

Opmerking
Zie ook Stelling 14 voor een ruimer geformuleerde eigenschap.
[einde Opmerking]

Klik hier Animatie voor een CabriJavapplet ter illustratie.
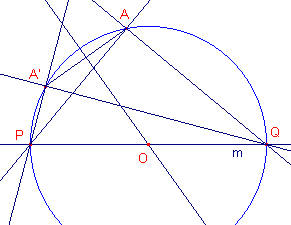
Hulpstelling 1
Bij een affiniteit (met as m) bestaan door elk punt A (met beeld A') twee loodrecht op elkaar staande lijnen, waarvan de beelden eveneens loodrecht zijn.

Bewijs:

figuur 3.2a figuur 3.2b
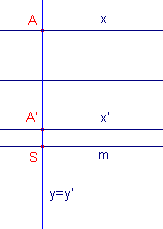affienc3a        affienc3b Staat AA' loodrecht op m (zie figuur 3.2a), dan zijn de lijnen x (loodrecht op AA') en x (de lijn AA') de gevraagde lijnen.
Is dit niet het geval (zie figuur 3.2b) dan tekenen we de middelloodlijn van AA' die m dan snijdt in het punt O. De cirkel met middelpunt O die door A en A' gaat snijdt m in P en Q. De lijnen PA en PB zijn nu de gezocht lijnen; de beelden daarvan zijn QA en QA'.
Deze lijnen staan loodrecht op elkaar (eigenschap van de Thales-cirkel op PQ). ¨
.
Stelling 13
Elke affiene afbeelding is het product van twee rechte lijnvermenigvuldigingen en een orthogonale afbeelding.

Bewijs:

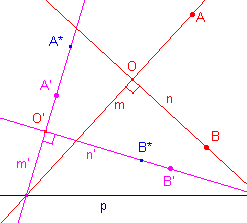affienc4 Zij O en O' twee toegevoegde punten van een affiene afbeelding T.
Nu is T op te vatten als het product van een gelijkvormigheidsafbeelding U en een affiniteit V: T = UV (zie Stelling 12).
Volgens Hulpstelling 1 zijn er bij de afbeelding V twee door O gaande loodrecht op elkaar staande lijnen m, n waarvan de beelden m', n' (gaande door O') eveneens loodrecht op elkaar staan.
Omdat U hoektrouw is, zijn de beelden van m en n onder de afbeelding T eveneens loodrecht.
Ligt nu A op m en B op n. Hun beelden onder T zijn A' en B'.
Er is nu een orthogonale afbeelding W (een translatie gevolgd door een rotatie) die O op O', m op m' en n op n' afbeeldt.
De beelden A* en B* van A en B onder W liggen dan opvolgend op m' en n'.

Zij nu L1 de rechte lijnvermenigvuldiging op m' die B* op B' afbeeldt en L2 de rechte lijnvermenigvuldiging op n' die A* op A' afbeeldt.
De produktafbeelding L1L2W beeldt dan driehoek OAB af op O'A'B'. Volgens Stelling 4 is dan T = L1L2W. ¨

Een direct gevolg van Stelling 13 is nu:

Stelling 14
Elke affiene afbeelding is het produkt van een lijnvermenigvuldiging en een gelijkvormigheidstransformatie.

Opmerking
Vergelijk deze stelling met Stelling 12 (met een beperkter geformuleerde eigenschap).
[einde Opmerking]

Bewijs:
We gebruiken hierbij de notaties uit Stelling 13.
De afbeelding L2 (de rechte lijnvermenigvuldiging op n') vervangen we door een homothetie G met centrum O' en factor k2 (= O'A'/O'A*).
De afbeelding L1 (de rechte lijnvermenigvuldiging op m', factor k1 = O'B'/O'B*) vervangen we door een lijnvermenigvuldiging X op m' met factor k1/k2.
G heeft hetzelfde effect op elk punt van m' als L2, en X en L1 laten m' puntsgewijs invariant.
XG heeft hetzelfde effect als L1L2 op elk punt van n'.
We hebben nu volgens Stelling 4: L1L2 = XG.
Maar ook geldt: (zie Stelling 12): T = L1L2W = XGW.
En de afbeelding GW is een gelijkvormigheidstransformatie, waaruit het gestelde blijkt.. ¨

5. Oppervlakte terug

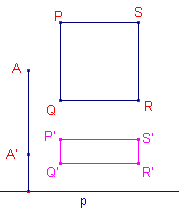
Stelling 15
Bij een affiene transformatie verandert de oppervlakte van een figuur met de factor k = k1k2, waarbij k1 en k2 de factoren zijn van twee rechte lijnvermenigvuldigingen als bedoeld in Stelling 13.

Bewijs:

affienc5 Volgens Stelling 13 is de affiene afbeelding T te schrijven als T = L1L2W, waarbij L1 en L2 rechte lijnvermenigvuldigingen zijn met factoren k1 en k2.
Onder W (een orthogonale afbeelding) verandert de oppervlakte niet.
Zijn s en s' de oppervlaktes van de figuur en de beeldfiguur, dan moet gelden s' = ks.
We beschouwen de oppervlakte van een vierkant(je) waarvan een van de zijden evenwijdig is met de affiniteitsas p van de afbeelding. Het beeld is dan een rechthoek.
In dit geval wordt alleen de "verticale" component vermenigvuldigd en de stellling is dus juist.

In het algemene geval bedekken we de figuur met een net van vierkantjes, waarvan de totale oppervlakte de waarde van s met een getal e overschrijdt. De beeldfiguur wordt dan overdekt met een net van rechthoeken, waarvan de oppervlakte tenminste gelijk is aan s'.

We hebben nu:  k(s + e) ³ s', voor iedere e, waaruit volgt dat ks ³ s' ......(1)
Voor de inverse afbeelding van T hebben we echter: (1/k)s' ³ s, zodat s' ³ ks ......(2)
Uit (1) en (2) volgt nu: s' = ks. ¨

6. Referenties terug

[1] P.S. MODENOV, A.S. PARKHOMENKO: Geometric Transformations, volume 1, Academic Press (New York, 1965)
[2] I.M. YAGLOM: Geometric Transformations, volume III, Random House (New York, 1973)

7. Download terug
De figuren die gebruikt zijn in de CabriJavapplets op deze pagina kunnen in éen bestand via deze website worden gedownload. Het bestand bevat ook enkele Cabri-macro's en andere figuren betrekking hebbend op affiene afbeeldingen.
Klik hier om het downloaden te starten (ZIP-bestand; ca. 24kB).

begin pagina
[affien.htm] laatste wijziging op: 27-12-04