Cabri werkblad

Overzicht  ][  Alle werkbladen | Meetkunde | Cabri

Overzicht - Trisectie van een koorde

Formulering van het probleem
Op een cirkel liggen twee vaste punten A en B.
We willen een koorde XY van de cirkel tekenen die door de lijnstukken MA en MB in drie gelijke stukken wordt gedeeld (dit heet ook wel trisectie).
figuur 1 triko1
  • Kies een nieuw Cabri werkblad en teken een cirkel met middelpunt M.
  • Teken A en B met de functie "Punt op object" in het Teken-menu.
  • Teken ook X en Y met deze functie.
  • Teken het lijnstuk XY en bepaal met de functie "Snijpunten" in het Punt-menu de snijpunten A’ en B’ van XY met opvolgend MA en MB (zie figuur 1)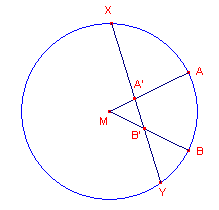

    • Cabri kent een functie waarmee je lengtes van lijnstukken kan bepalen. Deze functie, "Afstand en lengtes" vind je als eerste functie in het Berekeningen-menu (derde menu van rechts).

    • Selecteer met deze functie het punt X (Afstand van dit punt) en selecteer daarna het punt A’ (tot dit punt). Verplaats daarna de berekende waarde met de functie "Wijs aan" naar een buiten de tekening liggende plaats op je het werkblad.
    • Doe hetzelfde voor de lijnstukken A’B’ en B’Y (zie figuur 2)
    • Verplaats nu X en Y over de cirkel en bekijk daarbij de verandering in de afstanden.
    Opdracht 1 Ophalen van de figuur in Cabri Geometry       Animatie Animatie met CabriJava      (*)
    .
    (*) Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is geïnstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld.
    Voor animaties met     CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
    Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

    Bij het uitvoeren van de laatste opdracht heb je natuurlijk al geprobeerd de punten X en Y zo te plaatsen, dat XA’=A’B’=B’Y.
    Als dat niet direct gelukt is, probeer dan eerst de positie van X en Y zo te bepalen, dat XA’=B’Y (dat is iets gemakkelijker).

    figuur 2 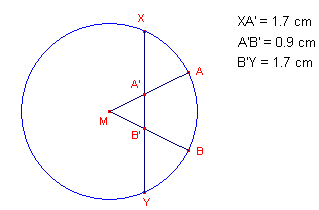triko2

    Opdracht 1

    Anders zoeken
    Mogelijk dat je uit opdracht 1 een andere manier van zoeken naar de juiste positie van X (en daardoor ook van Y) kunt afleiden.
    We geven hieronder in ieder geval een manier die aansluit bij opdracht 1.

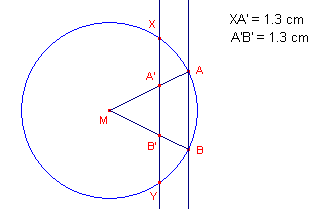    figuur 3 triko3

    Natuurlijk is dit niet de juiste manier van construeren van het punt X (en het punt Y).
    Er is in de eerste plaats sprake van een benaderde ligging van het punt X op de cirkel.
    Maar er is meer.
    Als je het punt A een andere positie op de cirkel geeft, dan moet het hele zoekproces opnieuw beginnen!
    Wat we natuurlijk willen, is een voorschrift (we noemen zoiets ook wel eens een algoritme) die bij iedere ligging van de punten A en B, de koorde tekent.

    Opdracht 2


    Bij het opstellen van een dergelijk algoritme moeten we natuurlijk de punten A en B (en daardoor ook de lijn AB) betrekken.
    Daarnaast hebben we het punt M.
    De vraag is nu dus: "Kunnen we, uitgaande van het punt M en de punten A en B, de ligging van het punt X vaststellen (construeren)?"
    Hebben we X eenmaal, dan is Y natuurlijk snel gevonden.
    Wat kunnen we dus nog meer doen, dan het tekenen van de lijn AB?

    De constructie


    Kijk nu eens naar figuur 4, die getekend is op basis van een constructie waarbij we de ligging van het punt X door "proberen" hebben vastgesteld (als in de paragraaf "Anders zoeken").
    figuur 4 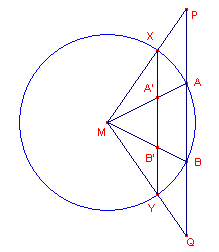triko4

    Opdracht 3
    a.   We weten nu, dat XA’=A’B’=B’Y en we weten ook, dat XY // AB.
    Bewijs nu, dat PA=AB=BQ.
    b. Mogen we deze eigenschap ook omdraaien?
    Met andere woorden:
    We weten, dat PA=PB=PC en dat PM en QM de cirkel opvolgend snijden in X en Y.
    Kan je nu bewijzen dat XA’=A’B’=B’Y?
    Probeer het eens!
    Aanwijzingen
    Wat voor soort driehoek is MPQ?
    Zijn de driehoeken MXY en MPQ gelijkvormig?
    Waarom is XY // AB?

    Op basis van opdracht 3, onderdeel b, kan je nu wel aangeven hoe je de punten X en Y, bij willekeurige ligging van de punten A en B, kan construeren.

    Opdracht 4

    a.  

    Voer een dergelijke constructie uit met behulp van Cabri.
    Aanwijzing
    De punten P en Q kunnen (bijvoorbeeld) worden gevonden met gebruikmaking van de functie "Puntspiegeling" in het Afbeeldingen-menu.

    b.

    Beschrijf kort hoe je de constructie hebt uitgevoerd.

    Tenslotte


    De onderstaande opdracht is facultatief.

    Opdracht 5

    a.  

    Ga na bij welke ligging van A en B op de cirkel er (in principe) geen oplossing van het probleem is.

    b.

    Maak een macro waarmee je op basis van de punten A en B op een cirkel de koorde XY direct kan tekenen.
    ad. a.
    Cabri geeft mogelijk wel een oplossing (afhankelijk van de opbouw van de macro).
    .
    Opdracht 1 Ophalen van de figuur in Cabri Geometry       Animatie Animatie met CabriJava

    Download
    De in het werkblad gebruikte Cabri-figuren kunnen via deze website in één bestand worden gedownload.
    In het bestand is ook de macro opgenomen waarmee de trisectie van een koorde kan worden geconstrueerd.
    Klik hier om het downloaden van het bestand te starten [9Kb, ZIP-formaat].

    Het werkblad zelf is ook in PDF-formaat beschikbaar:
    pdf triko.pdf [36Kb]

    begin pagina

    [triko.htm] laatste wijziging op: 26-02-2000