Cabri werkblad

Overzicht  ][  Alle werkbladen | Meetkunde | Cabri

---

Overzicht - Rakende cirkels

1. Cirkels die raken aan een gegeven cirkel
        Opdracht 1
2. Cirkels die raken aan twee gegeven cirkels
        Opdracht 2
        Opdracht 3

3. Download

---

1. Cirkels die raken aan een gegeven cirkel
We gaan uit van een cirkel met middelpunt M₁ (en straal r₁), waarbij M₁ op de lijn m ligt.
We zoeken nu cirkels met een gegeven straal r die inwendig en uitwendig raken aan de cirkel M₁ (zie figuur 1).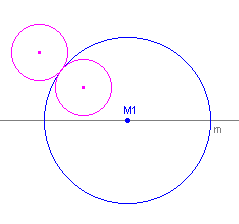

Opdracht 1

• Omschrijf de meetkundige plaats van de middelpunten van beide raakcirkels aan de cirkel M₁.

• Onder welke voorwaarde zijn er geen inwendig rakende cirkels?
• Is er een situatie denkbaar waarbij er geen uitwendig rakende cirkels zijn? Verklaar je antwoord.

2. Cirkels die raken aan twee gegeven cirkels
We borduren nu verder op paragraaf 1 door een tweede cirkel met middelpunt M₂ (en straal r₂) in onze beschouwing te betrekken.Ook M₂ ligt op de lijn m.
We bekijken nu cirkels (met een vaste straal) die de beide cirkels M₁ en M₂ inwendig of uitwendig raken (zie figuur 2).
We gaan er hierbij van uit dat de punten M₁ en M₂ niet samenvallen.

Opdracht 2

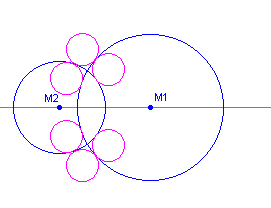• Ga na, dat in dit geval het aantal rakende cirkels maximaal 8 is.
• Ga na, dat er zeker geen rakende cirkels zijn als M₁M₂ > r₁ + r₂ + 2r.
• Wijzig alleen de positie van M1 en M2 en onderzoek het aantal en de positie van de rakende cirkels.
  Je kan dit uiteraard doen voor verschillende waarden van r.
• Zijn er precies 7 rakende cirkels mogelijk? Zo ja, onder welke voorwaarde.
  En 3 rakende cirkels?

Opdracht 3

• Probeer bij elk aantal rakende cirkels een voorwaarde te formuleren

3. Download
De hierboven behandelde figuren kunnen ook als één bestand via deze website worden gedownload.
Klik hier om het downloaden te starten [3Kb, ZIP-formaat].

---

[rakcirk.htm] laatste wijziging op: 22-04-2005