Cabri werkblad

Overzicht  ][  Alle werkbladen | Meetkunde | Cabri

---

Overzicht - Raaklijnen

1. Raaklijnen aan een cirkel
        Opdracht 1
        Opdracht 2
2. Euclides' constructie
        Opdracht 3
        Opdracht 4a
        Opdracht 4b
3. Een andere kijk op de raaklijn
        Opdracht 5
        Opdracht 6
4. Raaklijnen aan twee cirkels
        Opdracht 7
        Opdracht 8
        Opdracht 9
5. Download

Opmerking
Zie ook de webpagina "Raaklijnen", waarop een afwijkende constructie van de raakijnen aan twee cirkels wordt behandeld.

---

1. Raaklijnen aan een cirkel

Definitie Een raaklijn aan een cirkel is een rechte lijn die precies één punt (het raakpunt) met de cirkel gemeenschappelijk heeft.

Stelling De raaklijn in een punt op een cirkel staat loodrecht op de straal naar het raakpunt.

Bewijs:

figuur 1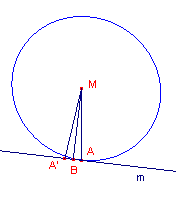

Zie figuur 1, waarin A op de cirkel met middelpunt M ligt, MA de raakstraal is en m de raaklijn in A aan de cirkel. We bewijzen deze stelling uit het ongerijmde. Stel m staat niet loodrecht op MA. We kunnen dan uit M de loodlijn op m neerlaten. We noemen het voetpunt van deze loodlijn B. Zij nu A' het spiegelbeeld van A in deze loodlijn, dan geldt A' ligt op m MA' = MA

Dus ook A' ligt op de cirkel. Maar dan heeft de lijn m twee (verschillende) punten gemeenschappelijk met de cirkel, hetgeen in tegenspraak is met het gegeven, dat m raaklijn is.
Hieruit volgt dus: MA ^ (loodrecht op) m. ¨

De constructie van een raaklijn aan een cirkel is, op basis van deze stelling, niet zo erg moeilijk meer.

Opdracht 1

figuur 2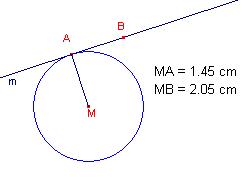

• Teken op een nieuw Cabri-werkblad een cirkel met middelpunt M en op die cirkel het punt A.
• Construeer op basis van bovenstaande stelling de raaklijn m in A aan de cirkel.
• Kies een punt B op de lijn m.
• Kies dan de functie "Afstand en lengte" in het Reken-menu en bepaal de lengte van het lijnstuk MA.
• Bepaal ook de afstand tussen de punten M en B (zie figuur 2)
• Ga door verplaatsing van het punt B op m na, dat steeds BM > BA, tenzij B met A samenvalt.

• Verklaar deze eigenschap met de stelling van Pythagoras.

Opdracht 2

• Hoeveel raaklijnen aan een cirkel gaan er door een punt A dat binnen die cirkel ligt?
  Verklaar je antwoord.
• Hoeveel raaklijnen aan een cirkel gaan er door een punt B dat buiten die cirkel ligt?
  Verklaar je antwoord.

2. Euclides' constructie
In het eerste boek dat over meetkunde geschreven is, de Elementen van Euclides (Euclides van Alexandrië, ~325 ­ ~265 vC), staat in Boek III in stelling 17 een manier waarop je een raaklijn uit een punt aan een cirkel kunt tekenen.

Opdracht 3

figuur 3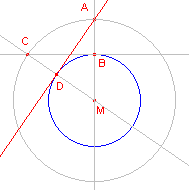

De door Euclides gegeven constructiestappen zijn:

1. Verbind A met het middelpunt M van de cirkel.
2. Teken de cirkel met middelpunt M en straal MA.
3. Teken in B (het snijpunt van AM en de eerste cirkel) de loodlijn op AM en bepaal een snijpunt C van die lijn met de tweede cirkel.
4. Verbind C met M en bepaal het snijpunt van CM met de eerste cirkel (zie figuur 3).
5. Verbind D met A.

Nu is AD een raaklijn (uit A) aan de eerste cirkel.

• Bewijs de juistheid van deze constructie.

De tweede raaklijn uit het punt A heb je met bovenstaande stappen nog niet gevonden.

• Geef aan hoe je, als je deze constructie zou uitvoeren met Cabri, snel ook de tweede raaklijn kunt vinden.

Opdracht 4a
Een constructie van de raaklijnen uit een punt aan een cirkel die gemakkelijker is uit te voeren, is gebaseerd op de stelling van Thales voor rechthoekige driehoeken. Deze luidt (zie ook figuur 4):

Stelling van Thales Van een rechthoekige driehoek is het midden van de schuine zijde het middelpunt van de omgeschreven cirkel.

figuur 4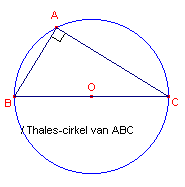

figuur 5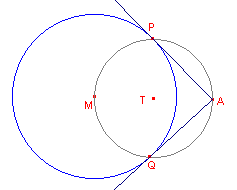

• Kies een nieuw Cabri-werkblad en teken opnieuw een cirkel met middelpunt M en een punt A buiten de cirkel (zie figuur 5).
• Teken de Thales-cirkel op AM (dat is de cirkel met middellijn AM; middelpunt T).
• Bepaal de snijpunten P en Q van beide cirkels.
• Teken de lijnen AP en AQ.

• Bewijs dat de lijnen AP en AQ raaklijnen zijn aan de cirkel.

Opdracht 4b - macro:RaaklijnenUitPunt

• Maak op basis van de constructie in Opdracht 4a de macro:RaaklijnenUitPunt, die, uitgaande van een gegeven cirkel en een punt, de beide raaklijnen tekent uit dat punt aan de cirkel.

• Beschrijf kort hoe je de macro hebt geconstrueerd. Vermeld ook de beginobjecten en eindobjecten.

• Controleer de werking van deze macro.

• Werkt de macro ook als je het punt op de cirkel kiest?
  Ga dit onder andere na door te controleren of je de (mogelijk) getekende raaklijn kunt snijden met een willekeurige andere lijn.
  Als er geen raaklijn getekend is, verplaats dan het betreffende raakpunt over de cirkel.
• (facultatief) Geef een verklaring waarom de macro niet goed werkt, als het punt op de cirkel ligt.

3. Een andere kijk op de raaklijn
Blaise Pascal was een wiskundige die leefde van 1623 tot 1662 in Frankrijk. Op zijn naam staat onder andere een stelling over kegelsneden, de naar hem genoemde stelling van Pascal.
Aangezien een cirkel een bijzondere kegelsnede (en wel een ellips) is, geldt deze stelling ook voor cirkels.
De stelling luidt:

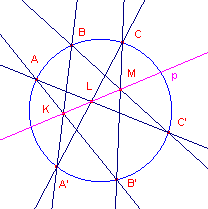We zullen deze stelling hier niet bewijzen, omdat daarvoor een aantal begrippen en eigenschappen nodig is dat boven de doelstelling van dit werkblad uitgaat.

Opdracht 5

• Teken een cirkel en kies daarop de punten A, B, C en A', B', C'.
• Bepaal de in de stelling van Pascal genoemde snijpunten K, L, M.
• Teken de lijn p door de punten K en L.

Je kan nu met Cabri controleren of het punt M ook op de lijn p ligt.

• Kies daartoe de functie "Ligt op...?" in het Eigenschappen-menu (dit is het vierde menu van rechts).

Selecteer het punt M en daarna de lijn p. Klik op een leeg deel van het werkblad. Als je de constructie goed hebt uitgevoerd, zie je "Dit punt ligt op het object".

• Verplaats enkele punten over de cirkel en stel vast, dat daarbij de "collineariteit" van K, L, M behouden blijft.

• Beschrijf wat er gebeurt met de lijn AB' als je het punt B' verplaatst naar de positie van A (of A verplaatst naar de positie van B').
• Welke punten moet je met elkaar laten samenvallen om drie raaklijnen aan de cirkel te krijgen?

Opmerking
Op basis van het bovenstaande is het nu zeker duidelijk dat men ook wel van een raaklijn aan een cirkel spreekt, als een lijn twee samengevallen snijpunten met die cirkel heeft.
[einde Opmerking]

Opdracht 6

figuur 7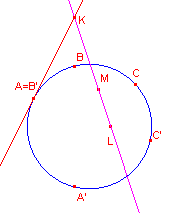

Op basis van de stelling van Pascal kan je nu ook een raaklijn in een punt aan een cirkel construeren.
Ga daarbij uit van de punten A, B, C en A', C' op een cirkel. Het punt B' valt dan samen met het punt A (zie figuur 7)

• Construeer op een nieuw Cabri-werkblad de raaklijn aan de cirkel in het punt A.
• Geef een beschrijving van de constructie (zie eerst de Aanwijzing).
  Aanwijzing
  Construeer eerst de punten L en M, en daarna het punt K

4. Raaklijnen aan twee cirkels
Je gaat nu de raaklijnen construeren aan twee cirkels.
In dit geval zijn er twee soorten te onderscheiden, uitwendige raaklijnen en inwendige raaklijnen.

Opdracht 7

• Zie figuur 8. Teken op een nieuw Cabri-werkblad twee cirkels (middelpunten M en N) die elkaar niet snijden. Kies de straal van cirkel N ongeveer 2 maal de straal van cirkel M.
• Teken een punt B op cirkel N en construeer (met een macro?) de raaklijn in B aan cirkel N.

We zullen deze raaklijn in deze opdracht aangeven met t.

• Teken ook de lijn MN (de centraal van beide cirkels).

figuur 8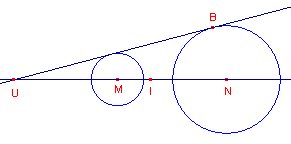

• Kies op de lijn MN twee punten (voorlopig zijn ze willekeurig) en noem zie U en I (de betekenis van deze letters is uit het bovenstaande wel af te leiden).
• Verplaats nu het punt B over cirkel N totdat t ook raaklijn is aan cirkel M.
• Als het snijpunt van t en MN buiten beide cirkels ligt, verplaats dan het punt U naar dit snijpunt.
  Als het snijpunt van t en MN tussen de beide cirkels ligt, verplaats dan het punt I naar dit snijpunt.

• Hoeveel posities van het punt B geven aanleiding tot een raaklijn aan beide cirkels?
• Wat kan je zeggen van de punten U en I met betrekking tot de gemeenschappelijke raaklijnen?

De raaklijnen die door U gaan heten uitwendige raaklijnen; de raaklijnen die door I gaan heten inwendige raaklijnen.

De vraag die nu hopelijk bij je opkomt is "Hoe kunnen we de plaats van de punten U en I op de lijn MN construeren?" (exact bepalen).
Immers, als we uit U (en I) raaklijnen t₁ en t₂ construeren aan de ene cirkel (bijvoorbeeld cirkel M ­en we weten hoe we dat moeten doen­), dan raken t₁ en t₂ automatisch aan de tweede cirkel (in dit geval dus aan cirkel N).
We onderzoeken een en ander in de volgende opdracht.

Opdracht 8

figuur 9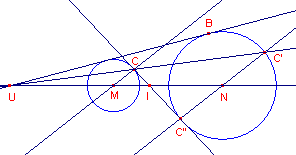

• Kies een willekeurig punt C op cirkel M en teken de lijn CM.
• Teken ook de lijn door N die evenwijdig is met CM.

Deze lijn heeft twee snijpunten met de cirkel N.
C' is het snijpunt waarbij de lijnstukken MC en NC' dezelfde "richting" hebben (zie figuur 9).
C" is het snijpunt waarbij de lijnstukken MC en NC" tegengestelde "richting" hebben.

• Teken de lijnen CC' en CC". Verander de positie van C op de cirkel M.

• Wat merk je nu op met betrekking tot de lijnen CC' en CC" in samenhang met de punten U en I?
• Formuleer nu een eigenschap van de punten U en I.
  Bewijs die eigenschap.
  Aanwijzing
  Gebruik gelijkvormige driehoeken.

Opmerking
De punten U en I heten opvolgend uitwendig gelijkvormigheidspunt en inwendig gelijkvormigheidspunt van de cirkels.
[einde Opmerking]

Opdracht 9

figuur 10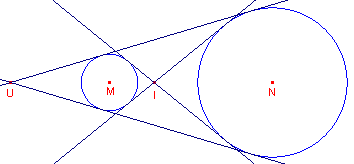

Als je uitgaat van twee gegeven cirkels, dan zijn de stappen voor de constructie van de gemeenschappelijke raaklijnen aan die cirkels dus de volgende:

1. Construeer het uitwendig en inwendig gelijkvormigheidspunt (zie Opdracht 8)
2. Construeer uit beide punten de raaklijnen aan één van beide cirkels (gebruik de macro:RaaklijnenUitPunt).

Deze raaklijnen zijn dan de gemeenschappelijke raaklijnen.

• Kies een nieuw Cabri-werkblad.
• Teken daarop twee cirkels.
• Construeer de gemeenschappelijke raaklijnen aan die cirkels.

We stellen het aantal gemeenschappelijke raaklijnen van twee cirkels gelijk aan k.

• Welke waarden kan k aannemen?
  Geef bij elk van de waarden van k een korte beschrijving en een tekening van de ligging van beide cirkels ten opzichte van elkaar.
• Er is een geval (of zijn er meerdere?) waarin je het uitwendig gelijkvormigheidspunt niet kan construeren, terwijl er daarbij toch twee uitwendige raaklijnen zijn.
  Beschrijf dat geval (die gevallen).

---

5. Download
De hierboven gebruikte Cabri-figuren en de behandelde macro's kunnen in één bestand via deze website worden gedownload.
Klik hier om het downloaden te starten [15Kb, ZIP-formaat].

Het werkblad is eveneens als PDF-bestand beschikbaar:
raaklijnw.pdf [62Kb]

---

[raaklijnw.htm] laatste wijziging op: 09-03-2000