Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri | Fractalen

Overzicht - Koch fractaal

Wat is een fractaal
Opdracht 1 - Trisectie van een lijnstuk
Opdracht 2 - Macro voor de trisectie van een lijnstuk
Opdracht 3 - 1^ste en 2^e benadering
Opdracht 4 - De kromme van Koch
Opdracht 5 - Sneeuwvlok-kromme
Opdracht 6 - Zelf doen
Download

Dit werkblad is gebaseerd op een deel van de lezing van Koen Stulens (Limburgs Universitair Centrum, Diepenbeek, België) onder de titel "Cabri Geometry II, Interactieve meetkunde op de PC" tijdens het Tweede T³-Symposium in Oostende (24-8-99 tot 26-8-99).

Wat is een fractaal
Een fractaal (Eng. fractal) is een meetkundige figuur waarin eenzelfde motief zich op steeds kleinere schaal herhaalt,
of ook wel
een fractaal is een (soms ingewikkelde) figuur, waarin men een zekere mate van zelfgelijkvormigheid kan aantreffen.

$lijnstukfrac$

De meest eenvoudige fractaal is misschien wel een lijnstuk.
Kopieer er een stukje uit (PQ) en dat stukje kan je door vermenigvuldiging met een bepaald getal weer even groot maken als het oorspronkelijke lijnstuk (AB).

Fractalen zijn figuren die "zelfgelijkvormig" zijn. Wat zelfgelijkvormigheid is staat eigenlijk in de hierboven staande zin:
elk deel kan door vermenigvuldiging afgebeeld worden op het geheel.

Maar er zijn ook ingewikkelder fractalen, zoals de "kromme van Koch".
Voor deze fractaal gaan we in het onderstaande een benadering maken.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

(*)

Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is geïnstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld.
Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

Opdracht 1 - Trisectie
Voorafgaand aan de constructie van de Koch fractaal behandelen we eerst een standaard constructie.
Bekijk de volgende figuur.

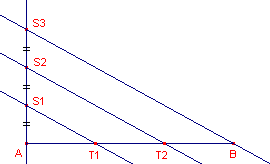
trisectlijnstuk

De constructiestappen van deze figuur zijn de volgende

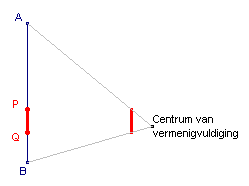
Teken lijnstuk AB.
Teken in A de loodlijn op AB. Kies op deze loodlijn het punt S₁, met "Punt op object" uit het Punt-menu.
Spiegel het punt A in het punt S₁, met "Puntspiegeling" uit het Afbeeldingen-menu.
Notatie: S₂ = Puntspiegeling(A, S₁).
Construeer S₃ als S₃ = Puntspiegeling(S₁, S₂)
Teken de lijn S₃B.
Teken de lijn door S₂ evenwijdig met S₃B en de lijn door S₁ evenwijdig met S₃B.
Bepaal de punten T₁ en T₂ met "Snijpunt(en)" uit het Punt-menu.

Voer bovenstaande stappen op een nieuw Cabri werkblad uit.
Bewijs, dat nu geldt AT₁ = T₁T₂ = T₂B.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

We hebben dus een lijnstuk in drie gelijk stukken verdeeld.
We zullen deze constructie ook in de toekomst nog wel eens gebruiken.
Daarom zullen we deze constructie gebruiken voor een macro.

Opdracht 2 - Macro

Verberg alle objecten in de figuur van Opdracht 1, met uitzondering van A, B, lijnstuk AB en de punten T₁ en T₂.
Kies "Beginobjecten" in het Macro-menu.
Selecteer het lijnstuk AB.
Kies "Eindobjecten" in het Macro-menu.
Selecteer de punten T₁ en T₂.
Kies "Definieer macro" in het Macro-menu.
Vul de de gegevens aan als in onderstaande afbeelding. Denk aan het selecteren van "Opslaan in bestand".

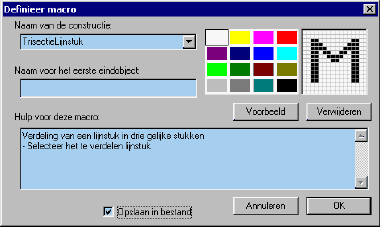
trisecmac

Bewaar de macro door op de knop OK de klikken.

Opdracht 3 - 1^ste en 2^e benadering

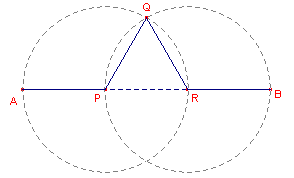
koch1mac

Teken het lijnstuk AB en gebruik de macro uit Opdracht 2 om AB in drie gelijke stukken te verdelen.
Teken vervolgens de cirkel met middelpunt P door A en de cirkel met middelpunt R door B.
Bepaal met "Snijpunt(en) uit het Punt-menu het "bovenste" snijpunt van de cirkels.
Hiermee ligt de oriëntatie die de ligging van S ten opzichte van AB bepaalt, vast (zie de Opmerking bij Opdracht 5)
Teken daarna in de genoemde volgorde de linstukken AP, PQ, QR en RB.
Construeer nu de macro "Koch1" als volgt
- Beginobjecten: het lijnstuk AB.
- Verberg dan het lijnstuk AB (met "Verberg/Toon" in het Layout-menu).
- Eindobjecten: de lijnstukken AP, PQ, QR en RB.
Sla deze macro op onder de naam Koch1.

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Met de macro Koch1 zijn we nu dus in staat een lijnstuk te vervangen door vier lijnstukken die elk ¹/₃ zijn van het oorspronkelijke lijnstuk.
Het nieuwe gebroken lijnstuk AB is de 1^ste benadering van de kromme van Koch.

Als het oorspronklijke lijnstuk AB = a, hoelang is dan het
gebroken lijnstuk AB?
Voer nu de macro Koch1 uit op de vier lijnstukken.
Hoelang is nu het gebroken lijnstuk AB?

Het nu ontstane gebroken lijnstuk noemen we de 2^de benadering van de kromme van Koch.

Hoe lang is, uitgaande van de 0-de benadering (het lijnstuk AB), de 3e benadering van de kromme van Koch?

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Opdracht 4 - De kromme van Koch
Om een snellere constructie te krijgen kan je, uitgaande van het lijnstuk AB, ook de 2^de benadering in een macro opnemen.
Dit zijn de constructiestappen:

Toon in de 2^de benadering (zie Opdracht 3) het oorspronkelijke lijnstuk AB.
Beginobjecten: selecteer het lijnstuk AB
Verberg het lijnstuk AB weer.
Eindobjecten: de 16 lijnstukken uit Opdracht 3.

Sla de macro op als Koch2.
Pas Koch2 toe op de 2^e benadering van de kromme van Koch.
Uit hoeveel lijnstukjes bestaat de benadering nu?
Je hebt nu de n^de benadering. Hoe groot is n ?

Opmerking
Het herhaald toepassen van de macro vraagt elke keer meer tijd. Dat komt doordat Cabri telkens meer berekeningen moet uitvoeren betrekking hebbend op de positie van de verschillende punten en lijnstukken (ook al zijn die verborgen).
[einde Opmerking]

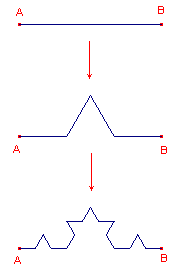
De kromme van Koch
Als we de macro (Koch1 of Koch2) herhaald uitvoeren, krijgen we elke keer een betere benadering van de kromme van Koch.

Als K_n de n^de benadering is, dan is

uiteindelijk de "echte" kromme van Koch.

De kromme is genoemd naar de Zweedse wiskundige Helge von Koch (Niels Fabian Helge von Koch, 1870-1924).

Wat is de lengte van de kromme van Koch?

Opdracht 5 - Sneeuwvlok-kromme

In de hiernaast staande figuur zie je een benadering van de zogenoemde Sneeuwvlok-kromme van Koch.

Ga met Cabri en de behandelde macro's na hoe deze uit een zekere regelmatige veelhoek kan ontstaan.
Geef een beschrijving van de stappen die tot deze figuur hebben geleid.
Welke benadering staat in de figuur hiernaast?
Uit hoeveel lijnstukjes bestaat de 1^ste benadering. En uit hoeveel de 2^e?
Hoeveel lijnstukjes heeft de n^de benadering?
Hoe groot is de omtrek van de Sneeuwvlok-kromme?
Ga uit van een oppervlakte 1 van het gebied binnen de 0^de benadering van de Sneeuwvlok-kromme.
Hoe groot is de oppervlakte binnen de 1^ste benadering? En binnen de 2^e?
Hoe groot is de oppervlakte binnen de Sneeuwvlok-kromme?

Ophalen van de figuur in Cabri Geometry

Animatie met CabriJava

Opmerking
Bij het uitvoeren van een macro is het soms noodzakelijk te letten op de oriëntatie van de figuur waarop de macro wordt toegepast.
Met de macro's Koch1 en Koch2 kan ook de hiernaast staande figuur ontstaan uitgaande van een bepaalde basisfiguur.
[einde Opmerking]

Opdracht 6 - Zelf doen
Je mag natuurlijk zelf ook een andere verdeling van een lijnstuk (of een figuur) bedenken die, herhaald toegepast, kan leiden tot een fractaal of tot een figuur die op een fractaal lijkt.
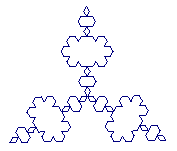
Twee voorbeelden

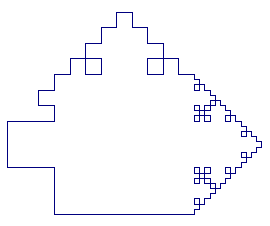gedeeltelijk uitgevoerd

Zeef van Sierpinski

Download
De hierboven behandelde figuren en macro's kunnen ook als één bestand via deze website worden gedownload.
Dat bestand bevat ook nog enkele andere Cabri-figuren, waaronder een figuur met de 5^e benadering van de kromme van Koch.
Klik hier om het downloaden te starten [35Kb, ZIP-formaat].

[koch.htm] laatste wijziging op: 22-11-1999