Raaklijnen aan een cirkel uit een oneigenlijk punt

Stelling 1 | Stelling 2 ][ Cabri-FAQ | Cabri | Meetkunde

Met Cabri kan worden geïllustreerd, dat (zie Vraag 9 op de pagina "Cabri-FAQ"):

Stelling 1
-	De raaklijnen uit een oneigenlijk punt aan een cirkel zijn evenwijdig.
-	De poollijn van een oneigenlijk punt gaat door het middelpunt van de cirkel.

We bekijken een en ander in figuur 1a en figuur 1b.

figuur 1a		figuur 1b

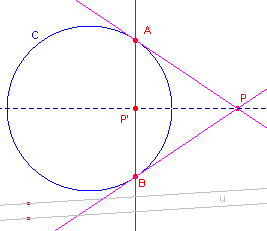
In figuur 1a zijn de raaklijnen uit P aan de cirkel C getekend. De raakpunten zijn A en B.
De lijn AB is de poollijn van P ten opzichte van de cirkel. P' is het midden van AB.

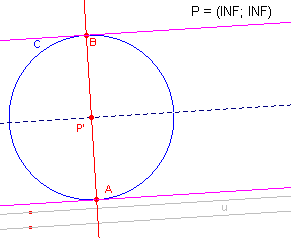
We hebben in figuur 1a het punt P opnieuw gedefinieerd als oneigenlijk punt van de lijn u.
Het resultaat daarvan staat in figuur 1b.

We zien in die figuur dat inderdaad P = (INF; INF), hetgeen duidt op een oneigenlijk punt (zie Cabri-FAQ: Vraag 9).
De raaklijnen in A en B hebben hetzelfde oneigenlijk punt (P), en zijn dus evenwijdig aan de lijn u.
AB is de verbindingslijn van de raakpunten; AB is dus de poollijn van het oneigenlijke punt P.
Eigenschap: De verbindingslijn van de raakpunten van twee evenwijdige raaklijnen aan een cirkel gaat door het middelpunt van die cirkel.
Uit deze eigenschap volgt:
In figuur 1b valt het punt P' samen met het middelpunt van de cirkel C.
De poollijn van P_inf gaat dus door het middelpunt van de cirkel.

Omgekeerd (zie Vraag 10 op de pagina Cabri-FAQ):

Stelling 2

De poollijn van het middelpunt van een cirkel ten opzichte van die cirkel is de oneigenlijke rechte.

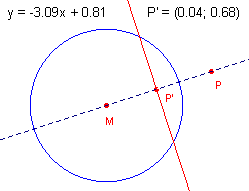
In de linker figuur is de poollijn van P tov. de cirkel M getekend. De vergelijking van de poollijn is eveneens weergegeven.
Daarna is het punt P opnieuw gedefinieerd als het punt M (het middelpunt van de cirkel).
Het resultaat staat in de rechter figuur.
De poollijn is nu de oneigenlijke rechte.

Opmerking
In de linker figuur is het punt P' bepaald met de Cabri-functie "Inversie" (in het Afbeeldingen-menu van Cabri).
De stippellijn in de linker figuur is de lijn door P en P'; en niet door P en M.
In dit laatste geval is de constructie namelijk niet uitvoerbaar, omdat dan na herdefiniëring van P de lijn MP onbepaald is.
[einde Opmerking]

[vgv_ad92.htm] laatste wijziging op: 09-07-01