TI-83 werkblad

Overzicht  ][ TI-werkbladen

Overzicht Logaritmen (1)

  1. Inleiding
  2. Machten
  3. Het getal 10 als factor
         Opdracht 1
         Opdracht 2
  4. De LOG-toets
         Opdracht 3
         Opdracht 4 met alog b = 10log b / 10log a

Download

Klik hier voor een vervolg op dit werkblad: Logaritmen (2) (ca. 140 kB; alleen beschikbaar in PDF-formaat).

1. Inleiding

 terug
We hebben afgesproken dat we de "wiskundige" uitspraken in de linker kolom kort kunnen schrijven.
Zie daarvoor de rechter kolom.
2 past 2 keer als factor in 4 2log 4 = 2
3 past 4 keer als factor in 81 3log 81 = 4
8 past 2 keer als factor in 64 8log 64 = 2
10 past 2 keer als factor in 100 10log 100 = 2
10 past 3 keer als factor in 1000 10log 1000 = 3

De factor 2 (als vermenigvuldigingsfactor) past 3 keer in het getal 10 (immers 23 = 8). Er blijft dan nog wat "ruimte" over.
Factor 2 past als het ware iets meer dan 3 keer in 10.
We hebben dus: 2log 10 = 3,...
We gaan met behulp van de GR preciezer bepalen hoe vaak.
We gebruiken daartoe eerst de machtsverheffing van de GR. De toets voor de machtsverheffing is

[ ^ ] (rechts op de machine; 6e toets van onder).

2. Machten terug
Zet nu je machine aan. Als er iets in het venster staat, druk dan op [CLEAR]. Hiermee wordt het venster gewist.

Druk daartoe achtereenvolgens [ 2 ] [ ^ ] [ 3 ] [ENTER].
De ENTER-toets werk dus als "is gelijk aan".
Je ziet dan: (>>>)		 log1-1
Let op dat je hierbij "onze" decimale komma vervangt door de decimale punt op de machine, de toets [ . ] .
Als je het goed gedaan hebt (en waarom niet), dan krijgt je: (>>>)

De machine berekent dus telkens de waarde in een "geschikt" (maar mogelijk ook telkens een ander) aantal decimalen.
Maar de uitkomst is nu bijna gelijk aan 10.

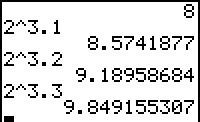 log1-2

Doe dat nog niet.

Want, zeker voor het vervolg, kunnen we handig gebruik maken van een "optie" (mogelijkheid) van de GR waarmee je de vorige opdracht kan opvragen.
Links boven de ENTER-toets staat ENTRY. Deze functie kan worden uitgevoerd door eerst op de 2nd-toets te drukken en daarna op de ENTER-toets.
Als je dat doet (dus druk op [2nd] [ENTER]), zie je: (>>>)

In het vervolg geven we dit aan met

[ENTRY] (dus niet met "[2nd] gevolgd door [ENTER]").		 log1-3
Verplaats nu de cursor met de toets [left] tot op de laatste 3 (zie figuur, >>>).
Druk daarna op [ 4 ], gevolgd door [ENTER].		 log1-4

Inderdaad, 23,4 is te groot (althans, het is groter dan 10).
We weten nu zeker, dat 2log 10 = 3,3... .
Wat is nu de volgende decimaal voor 2log 10?

  • Bereken zelf 23,31 ; 23,32 en 23,33. Maak daarbij gebruik van de ENTRY-toets!
  • Nu is dus: 2log 10 = 3,32... Waarom?
  • Bereken op dezelfde manier ook de derde en de vierde decimaal voor 2log 10.
Als je dat goed doet vind je tenslotte: (>>>)

Waarom weet je zeker, dat 9 echt de vierde juiste decimaal is van 2log 10?

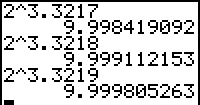 log1-5

3. Het getal 10 als factor

  terug
  • Zonder moeite zal je (en doe het zonder rekenmachine!) kunnen uitrekenen 10log 10, 10log 100, 10log 1000 en 10log 10.000.
  • Hoeveel is 10log 1047 en 10log (10
 n )?
  • Uit het bovenste rijtje volgt gemakkelijk, dat 10log 23 = 1,... en 10log 230 = 2,... . Waarom?
    •

    Opdracht 1


    Bereken op dezelfde manier als in paragraaf 2 (dus met behulp van machten) de eerste 3 decimalen van:
    a. 10log 23          (antwoord: 1,361...).
    b. 10log 230
    c. Al je dat goed gedaan hebt moet je bij het vergelijken van de antwoorden iets opvallen.
    Wat valt je op?
    d. Welk getal staat voor de komma bij 10log 2,3?
    Bereken nu ook de eerste 3 decimalen van 10log 2,3.
    Kan je het ook zonder je rekenmachine?
    e. Welk getal staat voor de komma bij 10log 230.000
    Bereken de eerste drie decimalen van 10log 230.000.

    Opdracht 2
    a. Waarom is 10log 5 = 0,...?
    Waarom is 10log 25 = 1,...
    b. Bereken 10log 5 en 10log 25, beide met de eerste drie decimalen.
    c. Valt je nu ook wat op?

    4. De LOG-toets

     terug
    Op de GR zit een toets waarmee je gemakkelijk 10-logaritmen van getallen kunt uitrekenen.
    Let wel alleen 10-logaritmen!
    Dat gaat met de toets     [LOG].
    Deze toets plaatst op het scherm echter automatisch een haakje achter log.
    Zie de figuur hiernaast. (>>>)    		 log1-6

    Wen eraan zelf steeds het sluithaakje -op de goede plaats- toe te voegen met

    [ ) ]¤ .
    Doe je dat niet, dan gaat de machine ervan uit, dat het sluithaakje helemaal aan het eind van de uitdrukking staat.
    • Bereken met de GR de uitkomsten van 10log 5 en 10log 25.

    10

    log 20 + 5 betekent: "bereken eerst het aantal keren dat 10 als factor in 20 past en tel er dan 5 bij op".
    10log (20+5) betekent: "bereken eerst 20+5 en kijk dan hoe vaak 10 als factor in die uitkomst past."
    Vergelijk eens de uitkomsten van 10log (20+5) en 10log 20 + 5. 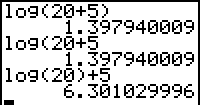log1-7

    Opdracht 3
    Bereken (zonder gebruik te maken van de GR) het getal voor de komma van
    10log 21415927
    Controleer met je GR.
     
    Bereken nu ook:
    10log 214159272 (gebruik hierbij     [x2] of [ ^ ] [ 2 ] ; zie figuur, >>>)
    10log 214159273

    Controleer je antwoorden met de GR.

    		 log1-8

    Opdracht 4


    Je hebt gezien, dat je met de machine eigenlijk alleen 10-logaritmen direct kunt uitrekenen.
    Hierboven (zie paragraaf  2) heb je gevonden
       2log 10 = 3,3219...
    Als je wat meer decimalen zou uitrekenen, vind je: (>>>) log1-9

    Inverse-toets

     - De toets [x -1] berekent het omgekeerde (de inverse) van een getal (dus "1 gedeeld door dat getal").
    Bekijk de werking van deze toets met de getallen in de figuur hiernaast: 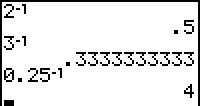log1-10
    Als je de uitkomst 4 op je scherm hebt staan, druk dan nog eens op [x -1].
    Je ziet dan dat de machine Ans op je scherm plaats met daarachter het inverse-teken.

    De machine geeft hiermee aan, dat de inverse-berekening wordt uitgevoerd met het laatste berekende getal (dat in de variabele Ans in het geheugen is opgeslagen).

    Druk je dan op

    [x -1] dan vind je dus weer 0,25.    		 log1-11
    a. Bereken ook de omgekeerden van 5 ; 0,125 ; 1/33 ; 0,142857.
    b. Bereken 10log 2 (gebruik dus de LOG-toets).
    c. Bereken dan het omgekeerde van 10log 2 (gebruik daarbij de x -1-toets).
    Wat valt je nu op, als je dit antwoord vergelijkt met de waarde van 2log 10 aan het begin van deze opdracht?
    Vul nu de volgende uitspraak aan: " 2log 10 is het ... van 10log 2 ".
    d. Bereken nu (en zet op je machine de haakjes op de goede plaats):
       10log 8 / 10log 2.    		 log1-12
    e. Hoe groot was ook alweer 2log 8?

    Je hebt nu een belangrijke regel ontdekt:

       

    log1-13
    f. Bereken nu met bovenstaande regel ook
       2log 1024
       3log 129140136
       5log 5
    g. Wat is de uitkomst van alog a?

    Download terug
    Het bovenstaande werkblad (met een iets afwijkende inhoud) is in PDF-formaat te downloaden via deze website (ca. 170 kB).
    Klik hier om het downloadproces te starten / IE-menu: rechtsklikken.

    N.b. Voor het lezen van zo'n bestand wordt het gebruik van Adobe Reader® geadviseerd >>> Get Reader

    begin pagina
    [log1-83.htm] laatste wijziging op: 12-02-2006