Zwaartevlakken, zwaartelijnen en bimedianen van een viervlak

Overzicht  ][  Stellingen | Overzicht Stereo | Gelijkzijdig viervlak

Overzicht terug

  1. Zwaartevlakken en zwaartelijnen cabri3dsignal
  2. Bimedianen cabri3dsignal
  3. Download

Zie ook de pagina "Gelijkzijdig viervlak" (in verband met bimedianen).
Zie ook het artikel "Het middenvlak (van een viervlak)" (PDF-formaat ca. 330 Kb).

1. Zwaartevlakken en zwaartelijnen terug

Definities terug
1. Het vlak door een ribbe van een viervlak en het midden van die overstaande ribbe heet zwaartevlak van dat viervlak.
2. De lijn door een hoekpunt en het zwaartepunt van het overstaande vlak van dat hoekpunt heet zwaartelijn (viervlakszwaartelijn).
.
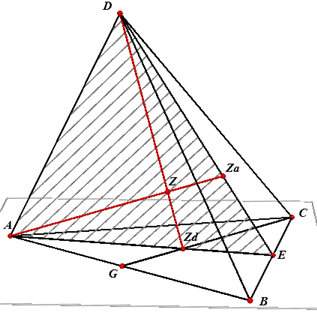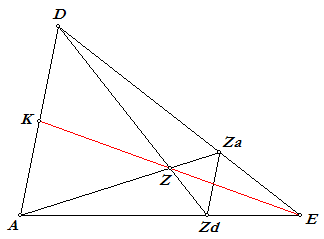
zwa1 In nevenstaande figuur is AED een zwaartevlak van viervlak ABCD en zijn de lijnen AZa en DZd viervlakszwaartelijnen (Za en Zd zijn de zwaartepunten van de zijvlakken DBC en ABC).

Hierbij zijn E en G de middens van de ribben BC en AB, waardoor AE en DE zwaartelijnen zijn van de zijvlakken BCD en ABD.
De viervlakszwaartelijnen AZa en DZd liggen daarmee dus in het zwaartevlak AED.

De lijnen AZa en DZd snijden elkaar in een punt Z.
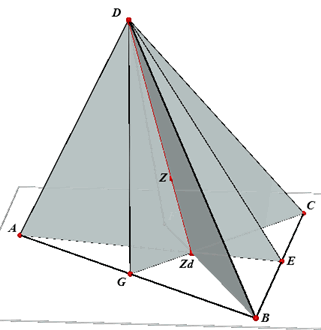
Stelling 1 terug
Alle viervlakszwaartelijnen snijden elkaar in hetzelfde punt Z, het zwaartepunt van het viervlak.
Daarbij is:
AZ : ZZa = BZ : ZZb = CZ : ZZc = DZ : ZZd = 3 : 1.

Bewijs. Elk tweetal zwaartelijnen is dus snijdend (zie de tekst hierboven; elk tweetal ligt in een zwaartevlak).
En deze zwaartelijnen liggen niet in hetzelfde vlak (immers, dan zouden A, B, C, D ook in hetzelfde vlak moeten liggen).
Volgens de Drie-lijnen-stelling gaan de (vier) zwaartelijnen AZa, BZb, CZc en DZd dus dooor hetzelfde punt Z.

zwa2 zwa3
Klik hier >Applet< voor een Cabri3D applet van de figuur links (opent in een nieuw Venster / Cabri3D plug-in noodzakelijk).
Klik hier >Applet< voor een Cabri3D applet van de figuur rechts (opent in een nieuw Venster / Cabri3D plug-in noodzakelijk).
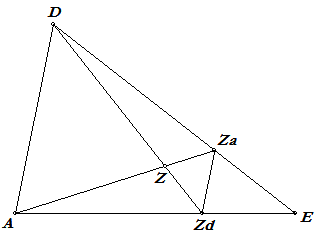zwa4 In het zwaartevlak AED geldt:
ZaE : ZaD = 1 : 2 (zwaartepunt Za op de zwaartelijn DE van driehoek BCD)
ZdE : ZdA = 1 : 2 (zwaartepunt Zd op de zwaartelijn AE van driehoek ABC)
Dan is ZaZd // AD, zodat:

AZ : ZZa = DZ : ZZd = 3 : 1 ¨
.
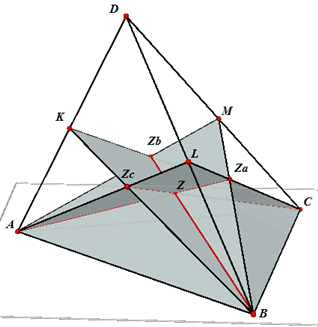
2. Bimedianen terug
Definitie terug
Een bimediaan van een viervlak is een lijn die de middens van twee overstaande ribben van dat viervlak verbindt.
.
Stelling 2 terug
De (drie) bimedianen van een viervlak gaan door het zwaartepunt Z van dat viervlak.
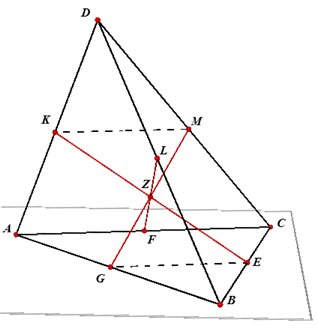zwa5 Bewijs.
De bimedianen EK en GM liggen in eenzelfde vlak omdat de lijnen KM en EG evenwijdig zijn (en dus dat vlak bepalen). Ze snijden elkaar in het punt Z.
Ook de bimedianen EK en FL snijden elkaar (volgens een analoge redenering).
Volgens de Drie-lijnen-stelling snijden ze elkaar dus in hetzelfde punt Z.

Klik hier >Applet< voor een Cabri3D applet van de figuur links (opent in een nieuw Venster / Cabri3D plug-in noodzakelijk).

Dat de drie bimedianen door het zwaartepunt Z van het viervlak gaan, blijkt hieronder.
zwa5b In driehoek AED is EK een bimediaan van het viervlak ABCD. Maar EK is eveneens zwaartelijn van driehoek AED.
De lijn EK gaat daarom door het snijpunt Z (zie ook het bewijs van Stelling 1) van de lijnen AZa en DZd, immers ZaZd // AD.
En dit geldt uiteraard voor elk tweetal bimedianen. ¨

3. Download terug
De op deze pagina gebruikte Cabri 3D applets kunnen in één bestand via deze website worden gedownload.
Klik hier >Download< om het downloadproces te starten (ZIP-bestand, ca. 15 Kb).

begin pagina
[p: zwaartevlak] laatste wijziging op: 15-10-2008 (13-10-2008)