Oppervlakte van een bol, bolsegment en bolschijf

Overzicht  ][  Inhoud bol  |  Overzicht Stereo  |  Cabri 3D

Overzicht terug

  1. Oppervlakte bol
  2. Naamgeving
  3. Oppervlakte bolsegment
  4. Oppervlakte bolschijf
¤. Zie ook de pagina "De bol".
¤ Zie evt. ook het artikel "Inhoud en oppervlakte van een bol zonder integraalrekening"
(Dick Klingens, sep. 2008, ongepubliceerd / PDF-bestand, ca. 380 Kb)

1. Oppervlakte bol terug

figuur 1
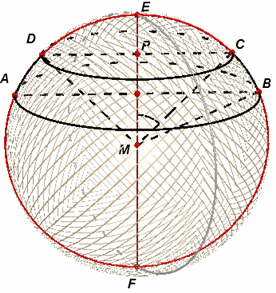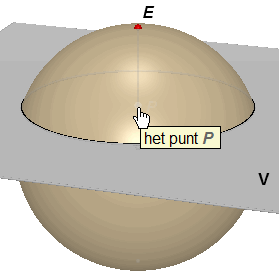
oppbol Om de oppervlakte van een bol met straal R te berekenen verdelen we de halve boog EBF (zie figuur 1) van een grote cirkel van de bol in n gelijke delen.
Door de deelpunten brengen we vlakken aan loodrecht op de (middel)lijn EF, die alle de bol volgens cirkels snijden.
Hierdoor wordt de bol in n delen verdeeld.

We beschouwen de oppervlakte van de bol als de limiet van de som van de ronde oppervlaktes van deze n delen als n naar oneindig nadert.

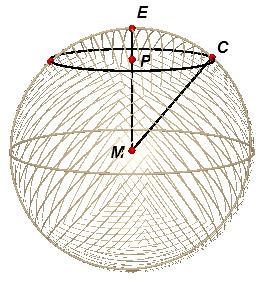
Als ABCD zo'n boldeel (een bolschijf) is, waarbij hoek EMC = fk en hoek CMB = Df, dan benaderen we de ronde oppervlakte daarvan met de oppervlakte van een rechthoek waarvan de breedte gelijk is aan de omtrek van de cirkel met middellijn CD en de hoogte gelijk is aan de lengte van boog CB. (De ronde oppervlakte van het het n-de boldeel wordt dus uitgevouwen tot een rechthoek.)

Omdat hoek EMC = fk is, is PC = R · sin(fk). Verder is dan bg(CB) = R · Df (de hoek op die boog, hoek CMB, is immers gelijk aan Df ).
Een benadering O' van de ronde oppervlakte van het boldeel ABCD is dan: O' = 2pR sin( fk ) · R · Df.
De oppervlakte O van de bol is dan gelijk aan:

oppbol(form1)

We hebben daarmee gevonden:

Stelling 1
De oppervlakte van een bol met straal R is gelijk aan 4pR2.

2. Naamgeving terug

figuur 2a - bolsegment figuur 2b - bolsector figuur 2c - bolschrijf
oppsegment oppsector oppschijf
Een boldeel dat begrensd worden door het boloppervlak en een plat vlak, heet bolsegment (een vlak V verdeelt de bol dus in twee bolsegmenten).
De hoogte van een bolsegment is het binnen het segment gelegen deel van de loodlijn op het snijdende vlak gaande door het middelpunt van de gemeenschappelijke cirkel.
In de figuur is dat het lijnstuk EP.		 Het deel van de bol dat ontstaat door de cirkelsector MCE te wentelen om de lijn EM, heet een bolsector.
Ook hier is EP de hoogte van de bolsector.

Nb. De oppervlakte van het boldeel bepaald door wenteling van de boog CE om EM is hier gelijk aan het bij de bolsector behorende bolsegment.

 Het boldeel ABCD dat begrensd wordt door het boloppervlak en door twee evenwijdige vlakken, heet een bolschijf.
De afstand P1P2 van de twee evenwijdige vlakken heet de hoogte van de bolschijf.

3. Oppervlakte bolsegment terug

Voor de oppervlakte O van het bolsegment gaan we op dezelfde manier te werk als voor de oppervlakte van de bol. We hebben dan hier (met PE = h):

oppbol(form2)

Nu is verder (zie figuur 2b): cos(fk) = MP / R = (ME - PE) / R = (R - h) / R, zodat:

oppbol(form3)

Zodat:

Stelling 2
De oppervlakte van een bolsegment van een bol met straal R is gelijk aan 2pRh, waarbij h de hoogte is van dat bolsegment.

4. Oppervlakte bolschijf terug

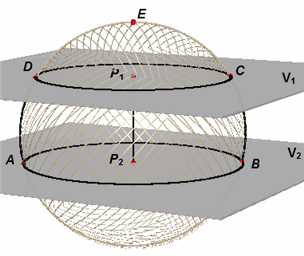
De oppervlakte O van een bolschijf met hoogte h kunnen we gemakkelijk vinden door het verschil te nemen van twee bolsegmenten (zie figuur 2c).
Volgens Stelling 2 hebben we dan voor de oppervlakte O1 van het bolsegment dat hoort bij P1( P1E = h1): O1 = 2pRh1
en voor de oppervlakte O2 die hoort bij P2 (P2E = h2) geldt: O2 = 2pRh2
Daarbij is h = P2P1 = h2 - h1, zodat:

Stelling 3
De oppervlakte van een bolschijf van een bol met straal R is gelijk aan 2pRh, waarbij h de hoogte is van die bolschijf.

up
[p: oppbol.htm] laatst gewijzigd op: 12-10-2008 (16-09-2008)