Lijn loodrecht op (twee snijdende lijnen in) een vlak

[ Overzicht stereo | Cabri 3D ]

Definitie
Onder de hoek tussen twee kruisende lijnen l en m verstaan we de scherpe hoek tussen de lijnen l' en m' die door een willekeurig punt P gaan waarbij l' // l en m' // m.

Zie eventueel de pagina "Definities".

Stelling 1
Staat een lijn loodrecht op twee snijdende lijnen in een vlak, dan staat die lijn loodrecht op elke lijn in dat vlak.

Bewijs:

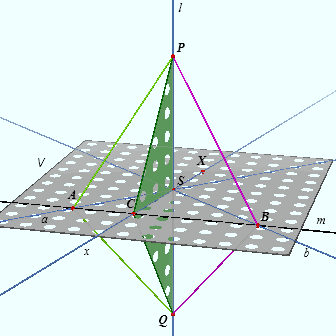In het vlak V liggen de elkaar in het punt S snijdende lijnen a en b. De lijn l staat loodrecht op a en loodrecht op b.
We nemen daarbij eerst aan dat de lijn l de lijnen a en b in S loodrecht snijdt
We nemen ook aan dat de lijn x door S gaat.
We bewijzen nu dat l ook loodrecht staat op x.

Kies op l de punten P en Q met PS = QS. En kies op a het punt A en op b het punt B.
De lijn x snijdt de lijn AB in het punt C.
Nu zijn de driehoeken ASP en ASQ congruent (ZHZ) en datzelfde geldt voor de driehoeken BSP en BSQ (ZHZ).
Uit die congruenties volgt dat AP = AQ en dat BP = BQ.
De driehoeken ABP en ABQ zijn dus eveneens congruent (ZZZ) waaruit volgt dat PC = QC.
En dan zijn ook de driehoeken CSP en CSQ congruent (ZZZ) waaruit volgt dat hoek CSP = hoek CSQ = 90°.
De lijn l staat dan loodrecht op de lijn x.

Gaan de lijnen l en x niet door het punt S, dan kunnen we via lijnen l' // l door S en x' // x door S op basis van het bovenstaande besluiten tot:
l' _|_ x'
En dan volgt (op basis van de definitie van de hoek tussen twee kruisende lijnen): l _|_ x. ¨

Klik hier >< voor een Cabri 3D applet bij de stelling.

We geven nu (gezien de stelling) de volgende definitie:

Definitie
Een lijn staat loodrecht op een vlak als die lijn loodrecht staat op elke lijn in dat vlak.

Opmerking
Moeten we bewijzen dat een lijn loodrecht staat op een vlak, dan is het dus volgens bovenstaande stelling voldoende te bewijzen dat die lijn loodrecht staat op twee elkaar snijdende lijnen in dat vlak.
[einde Opmerking]

Stelling 2
Als één van twee evenwijdige rechte lijnen loodrecht op een vlak staat, dat staat de andere er ook loodrecht op.

Bewijs:

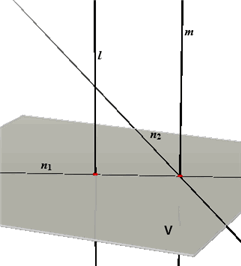Stel l staat loodrecht op V en l // m.

En daarmee staat l loodrecht op elke lijn in V (zie Definitie), en dus loodrecht op twee elkaar in het snijpunt van m met V snijdende lijnen n₁ en n₂.
Omdat m // l is, staat m ook loodrecht op n₁ en n₂ (zie Stelling 2). Volgens Stelling 1 staat m daarmee ook loodrecht op V. ¨

Stelling 3
Door een punt P gaat precies één lijn die loodrecht staat op een vlak V.

Bewijs:

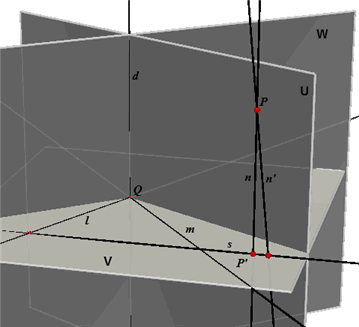Zijn l en m twee elkaar in het punt Q snijdende lijnen in het vlak V. Het vlak U gaat door Q en staat loodrecht op l (*) en het vlak W gaat door Q en staat loodrecht op m. De snijlijn d van de vlakken U en W staat dan loodrecht op l en ook loodrecht op m. Dus: d staat loodrecht op V.
De lijn n door P die evenwijdig is met d voldoet dan volgens Stelling 2 aan de eis.

Stel verder dat n' een tweede lijn is door P loodrecht op op V.
Het vlak X door n en n' snijdt dan het vlak V volgens een rechte lijn s. In X staan er dan twee rechte lijnen door P loodrecht op de lijn s. Hetgeen volgens de vlakke meetkunde niet mogelijk is.

Er is dus precies één lijn door P die loodrecht staat op het vlak V. ¨

(*) Opmerking. Het bestaan van een vlak W dat in het punt Q (gelegen op l) loodrecht staat op de lijn l, kan door constructie worden aangetoond.

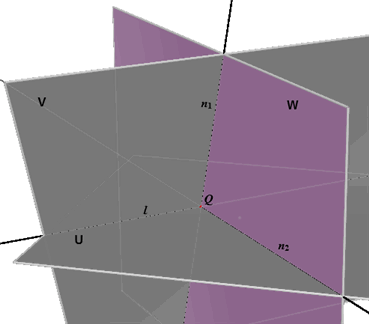Breng door de lijn l (en dus door Q) twee vlakken U en V aan en construeer in het punt Q in vlak U de lijn n₁ loodrecht op l en in vlak V de lijn n₂ loodrecht op l.
Het vlak W door de elkaar in Q snijdende lijnen n₁ en n₂ staat dan volgens Stelling 1 loodrecht op de lijn l.
[einde Opmerking]

[p: lijnloodrechtopvlak.htm] laatste wijziging op: 08-02-2018 (26-09-2005)