Wig van Wallis (2)

De wig van Wallis (2)

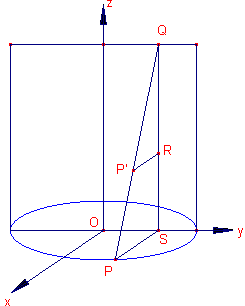We gaan uit van een orthonormaal assenstel Oxyz waarbij de cirkel in het xOy-vlak de vergelijking x² + y² = r² heeft, met r = ¹/₂d.
Voor een punt P van de cirkel hebben we dan:
   x = r.cosj, y = r.sinj, z = 0
Voor het punt P' op hoogte h dat op de mantel van de wig ligt, geldt in ieder geval:
   y = r.sinj, z = h
In driehoek PQS hebben we:
   QR : QS = P'R : PS
   (d - h) : d = x(P') : (r.cosj)
Zodat x(P') = r(d - h).cosj / d.
De x-coordinaat van P wordt dus vermenigvuldigd met (d - h)/d.
De oppervlakte pr² = ¹/₄pd² van de cirkel dus ook.

Voor de inhoud W van de wig vinden we dus: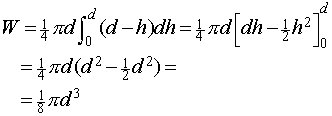
wallisform

Nemen we aan, dat de wig een kracht van 1 N uitoefent in de richting van de y-as, dan geldt voor het moment M tov. de oorsprong: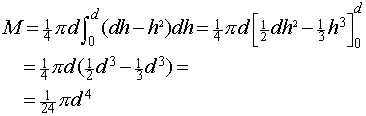
wallisform2

Voor het zwaartepunt Z van de wig, dat gelegen is op de z-as, hebben we dan:
W.z = M
waaruit volgt dat z = ¹/₃d .

[wig_wallis2.htm] laatste wijziging op: 27-12-04