|
De wig van Wallis |
||||||
 |
John Wallis (1616-1703, Engeland) was een van de oprichters
van de Royal Society in Londen. Hij heeft onder meer bijgedragen aan de ontwikkeling van
de differentiaal- en integraalrekening en was de meest invloedrijke wiskundige voor
Newton. Naar hem is ook het product (2.2.4.4.6.6.8.8.10..)/(1.3.3.5.5.7.7.9.9...) = p/2 genoemd. |
||||||
|
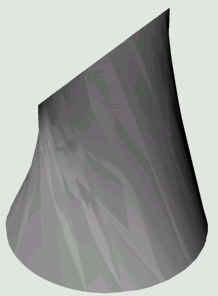
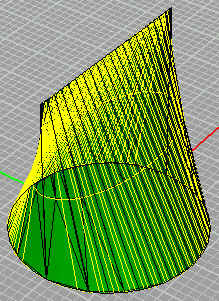
De wig van
Wallis ontstaat uit een cirkel met diameter d en een lijnstuk met lengte
d, waarvan het midden loodrecht ligt boven het middelpunt van de cirkel, en wel
op hoogte d. De beschrijvenden van de wig zijn alle evenwijdig aan het middelloodvlak van het lijnstuk en verbinden een punt van het lijnstuk met een punt van de cirkel. De doorsneden van de wig met een vlak evenwijdig aan het vlak van de cirkel zijn ellipsen. Klik hier voor een berekening van de inhoud en het zwaartepunt van de wig. |
||||||
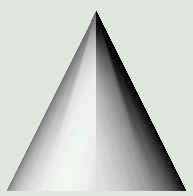
Hieronder staan
enkele aanzichten van de wig.
|
[wig_wallis.htm] laatste wijziging op: 27-12-04