Stelling van Morley [1]
Inleiding | 1e Bewijs | 2e bewijs ][ DK & Meetkunde
1. Inleiding
In 1899 ontdekte Frank Morley
(1860-1937, Woodbridge, Engeland), toendertijd verbonden aan het Quaker College in
Haverford (Pennsylvania, US), een verrassende eigenschap in een driehoek:
| Stelling De drie snijpunten van de aanliggende trisectrices van de hoeken van een driehoek vormen een gelijkzijdige driehoek. In dit verband heeft "aanliggend" de betekenis "aanliggend aan dezelfde zijde van de driehoek". |
In figuur 1 wordt de gelijkzijdige driehoek PQR gevormd door de trisectrices AQ en AR, BR en BP, CP en CQ.
| figuur 1 | 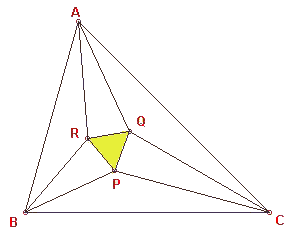 |
Morley's oorspronkelijke bewijs kwam voort uit onderzoek naar
algebraïsche krommen die raken aan een gegeven aantal lijnen. Zoals gebruikelijk in de wiskunde zijn er diverse pogingen gedaan om een elementair bewijs van deze stelling te leveren Een direct bewijs echter levert bijna onoverkomelijke problemen op. Daarom als eerste maar een indirect bewijs. |
2. Het 1e bewijs
Bewijs 1:
Op de zijden QR, RP, PQ van een gelijkzijdige driehoek worden PQR (zie figuur 2) worden
(uitwendig) gelijkbenige driehoeken P'RQ, Q'PR, R'QP geconstrueerd, en wel zo, dat de
basishoeken a, b, c van die driehoeken voldoen aan
a + b + c = 120º, a < 60º, b < 60º, c < 60º
| figuur 3 | 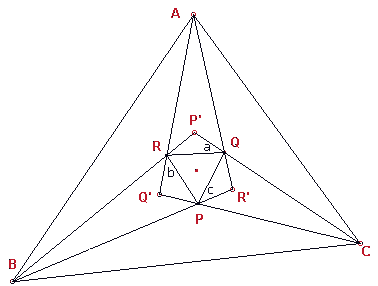 |
figuur 4 | 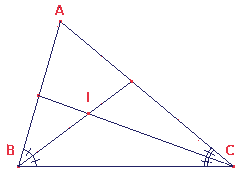 Voor het middelpunt I van de ingeschreven
cirkel van een driehoek geldt, dat |
Daarna worden de benen van die driehoeken verlengd tot ze elkaar snijden in de punten
A, B, C.
Omdat nu a + b + c + 60º = 180º, volgt nu voor bijvoorbeeld driehoek ARQ, dat
h(A van ARQ) = 60º - a, omdat de hoeken bij Q en R opvolgend gelijk zijn aan
a + b en a + c.
Nu is de lijn PP' een diagonaal van de vlieger PQP'R. Dus de halve hoek bij P' is gelijk
aan 90º - a. Verder is h(BPC) = 180º - a = 90º + (90º - a).
Hieruit mogen we volgens de eigenschap vermeld in figuur 4 dus concluderen, dat P het
middelpunt van de ingeschreven cirkel is van driehoek P'BC.
Hetzelfde geldt dus voor het punt Q voor driehoek Q'CA en R voor R'AB.
Hieruit volgt dus, dat alle kleine hoeken bij A, B, C aan elkaar gelijk zijn. Met andere
woorden de hoeken bij A,B,C van driehoek ABC worden in drie gelijke stukken verdeeld.
De drie kleine hoeken bij A zijn alle gelijk aan 1/3h(A) = 60º - a.
zodat
a = 60º - 1/3h(A), b = 60º - 1/3h(B), c = 60º - 1/3(C)
Kiezen we nu deze waarden voor de basishoeken van de drie gelijkbenige driehoek, dan zijn we ervan verzekerd, dat er via de beschreven procedure een driehoek ABC ontstaat die gelijkvormig is met een willekeurige gegeven driehoek ¨
3. Het 2e bewijs
Klik hier voor een bewijs met behulp van goniometrie.
[morley.htm] laatste wijziging op: 27-10-2000