Een minimaliseringsprobleem

Probleemstelling | Formules | Oplossing | Illustratie  | Download ][  Analyse

---

Probleemstelling - minimale oppervlakte van een cilinder bij vaste inhoud

figuur 1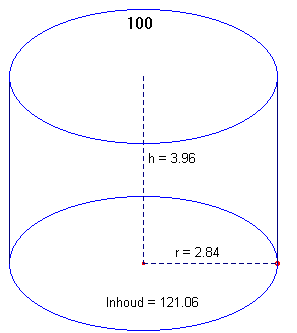

Gegeven is een cilinder met een vaste inhoud, zeg 100 cm3. Bij welke straal van de grondcirkel is de oppervlakte van de cilinder (manteloppervlakte plus oppervlakte van de beide grenscirkels) minimaal?

Formules

De straal van de grondcirkel zij r, de hoogte h.

Inhoud:	V = p r2h
Manteloppervlakte:	M = 2p rh
Beide cirkels:	C = 2p r2
Totale oppervlakte:	O = C + M = 2p r2 + 2p rh = 2p r(r + h)

Oplossing

Omdat de inhoud bekend is, drukken we de hoogte h uit in r en V:
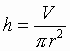    (zie formule voor M)
en substitueren die waarde in de formule voor O:
   
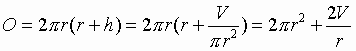
Hierdoor is O een functie O(r) van r.
Omdat we een minimum van die functie willen berekenen, bepalen we de afgeleide O’ naar r van O:
   
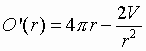
Vervolgens bepalen we het tekenschema van O’. Hiertoe lossen we eerst de volgende vergelijking op:
   
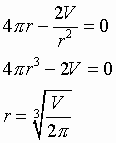
Voor "grote" waarden van r is O’(r) > 0, zodat we het volgende tekenschema krijgen:

	O’(r)	?	– – – – – –	0	+ + + + + +
	r	0		(V/2p )1/3

We vinden dus inderdaad een minimum van O voor de berekende waarde van r.

Voorbeeld

Voor V = 100 cm³:
r = 2,52 cm, h = 5,03 cm
waardoor dus de minimale oppervlakte O(r) = 119,27 cm².
[einde Voorbeeld]

Illustratie

figuur 2		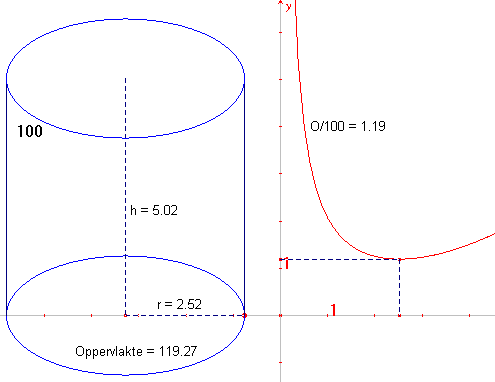In de figuur hiernaast is de grafiek getekend van de functie O, op basis van een volume V van 100 cm3. Deze grafiek is gegenereerd met het programma Cabri Geometry II.
figuur 3		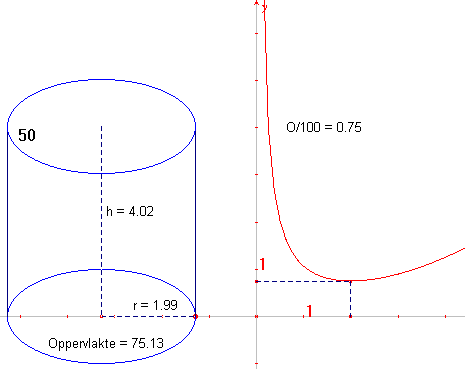Voor V = 50 cm3 krijgen we een grafiek als in figuur 3. Klik hier voor een CabriJavapplet hierbij.

Download

Klik hier voor het ophalen van de Cabri-figuur [ZIP-bestand, ca. 3 Kb]. In dit bestand zijn mogelijk ook andere figuren opgeslagen.

---

[minopp.htm] laatste wijziging op: 18-01-18