Concurrente middellijnen bij snijdende cirkels

Inleiding | Stelling  ][  Inversie | DK & Meetkunde

1. Inleiding
Inversie kan (uiteraard) vaak worden toegepast bij het bewijzen van meetkundige eigenschappen die te maken hebben met cirkels en lijnen.
Het bewijs van die eigenschappen verloopt daardoor vaak bijzonder eenvoudig.
We geven hieronder een voorbeeld.

2. Stelling

Gegeven zijn de elkaar in de punten A en B snijdende cirkels K1 en K2.
De middellijn van K1 door B snijdt K2 ook in het punt C; de middellijn van K2 door B snijdt K1 ook in D.
K3 is de cirkel door B, C en D.
De lijn door A en het middelpunt van K3 gaat dan ook door het punt B.
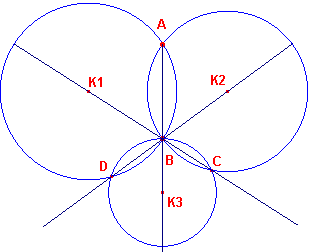      figuur 1 midcirkels

Bewijs met behulp van inversie (zie figuur 2):

figuur 2  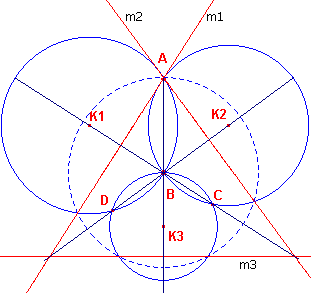midcirkels2 We kiezen het punt B als centrum van inversie, waarvan de inversiecirkel door het punt A gaat.
De cirkels K1, K2 en K3 gaan nu over in rechte lijnen (m1, m2, m3) die elkaar twee aan twee snijden. Deze rechte lijnen vormen dus een driehoek, verder "beelddriehoek" genoemd.
De lijnen BK1, BK2 gaan in zichzelf over. Evenals de lijn AK3.
De lijn BC snijdt de cirkel K1 loodrecht. BC staat dus ook loodrecht op m1 (inversie is hoektrouw).
BC is dus hoogtelijn van de beelddriehoek. Dit is ook het geval met BD.
Het punt B is dus hoogtepunt van de beelddriehoek.
Om dezelfde reden staat de lijn AK3 loodrecht op m3.

De lijn AK3 gaat dus eveneens door B.  ¨

begin pagina

[midcirkels.htm] laatste wijziging op: 16-07-1999