Negenpuntcirkel (eenvoudig bewijs)

Negenpuntscirkel

Bewijs ][ Stelling van Feuerbach | Meetkunde

Zie ook: Cabri-werkblad / Negenpuntscirkel

Over de Negenpuntscirkel

Stelling
De middens van de zijden, de voetpunten van de hoogtelijnen en de middens van de "bovenste stukken" van de hoogtelijnen van een driehoek liggen op een cirkel.

Onderstaand volgt een bewijs van deze stelling gebaseerd op gelijkvomigheid en de macht van een punt tov. een cirkel (zie ook de pagina "Over de cirkel van Feuerbach...").

Bewijs:

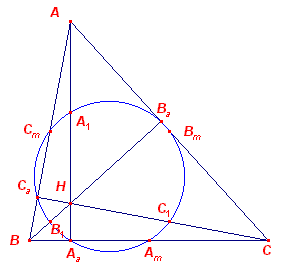A_a is het voetpunt van de hoogtelijn uit A, A_m is het midden van de overstaande zijde van A, H is het hoogtepunt, A₁ is het midden van AH ("bovenste stuk van de hoogtelijn"); etc.
Nu is: BCC_a ~ BAA_a
BA_a : BC_a = BA : BC = BC_m : BA_m
BA_a · BA_m = BC_a · BC_m
A_a, A_m, C_a, C_m zijn concyclisch
Verder is: CHA_a ~ CBC_a
CH : CA_a = CB : CC_a
CC₁ : CA_a = CA_m : CC_a
CC₁ · CC_a = CA_a · CA_m

C₁ ligt op de cirkel door C_a, A_a, A_m
Met andere woorden: A_a, A_m, C_a, C_m, C₁ zijn concyclisch.
Analoog: A_a, A_m, C_a, C_m, A₁ zijn concyclisch.
Zodat: A_a, A_m, C_a, C_m, A₁, C₁ zijn concyclisch.
Analoog: A_a, A_m, B_a, B_m, A₁, B₁ zijn concyclisch.
En hieruit vinden we: A_a, A_m, A₁, B_a, B_m, B₁, C_a, C_m, C₁ zijn concyclisch. ¨

¤ Terug naar de pagina "Over de cirkel van Feuerbach ..."

[feuerbach3.htm] laatste wijziging op: 19-10-07