Scheve projectie

Inleiding | Download ][ Stellingen | Overzicht stereo

Inleiding
Om een juiste indruk (afdruk, of een juist beeld) van 3-dimensionale figuren te krijgen (hetzij op papier, hetzij op beeldscherm) is het noodzakelijk deze figuren af te beelden (te projecteren) op een plat vlak. In hetgeen volgt wordt de belangrijkste afbeeldingsmethode behandeld, de scheve projectie.

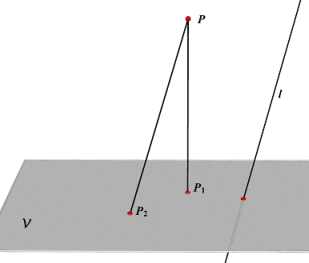Definities
1. Onder de orthogonale projectie P₁ van een punt P op een vlak V verstaan we het voetpunt van de loodlijn uit P op V.
2. Doorloopt het punt P een ruimtelijke figuur L, dan is de meetkundige plaats van de orthogonale projectie P₁ van P de orthogonale projectie van de figuur L.

De orthogonale projectie behoort tot de klasse van zogenoemde parallelprojecties.
Het is ook mogelijk een figuur L op een vlak V te projecteren met lijnen die een vaste richting hebben (niet loodrecht op V ). Een dergelijke projectie noemen we scheve projectie (ook wel scheve parallelprojectie).De vaste projectierichting wordt meestal bepaald door een rechte lijn of door het geven van een ruimtelijk punt P en het daarbij behorende beeldpunt P₂ in het platte vlak V.

We gebruiken bij de afbeeldingen twee loodrecht op elkaar staande vlakken H, het horizontale vlak, en T, het tafereel.
We bekijken dan een orthogonale projectie op H en een scheve projectie op T.

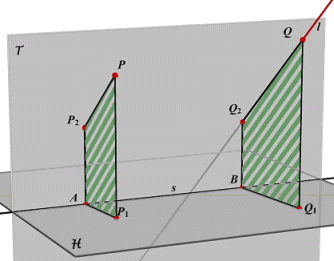In de figuur hiernaast is de scheve projectie in de richting van de lijn l (bepaald door Q niet in H of T, en Q₂ wel in T) ook toegepast op het punt P.
De lijn s is de snijlijn van H en T.

De orthogonale projectie van P op H is P₁ en de scheve projectie van P op T is P₂.

Nu is:
PP₁ ^ H en QQ₁ ^ H, zodat PP₁ // QQ₁
De punten A en B liggen zó op de snijlijn s van H en T, dat:
P₁A ^ s en Q₁B ^ s
De lijn s staat daarmee loodrecht op de vlakken AP₁PP₂ en BQ₁QQ₂, waardoor die vlakken evenwijdig zijn.

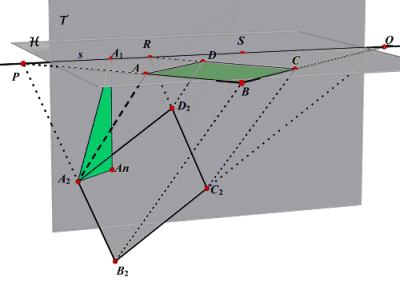Hiernaast is de scheve projectie A₂B₂C₂D₂weergegeven van een in H gelegen vierkant ABCD.

Download
Voor de theorie achter de scheve projectie wordt verder verwezen naar het artikel "Scheve projectie" (PDF-bestand, ca. 300 KB).

In de theorie worden onder meer bij scheve projectie gebruikte termen als projectiedriehoek, verkortingsverhouding en wijkhoek toegelicht.
Ook worden enkele constructievoorbeelden gegeven.

[p: schepro.htm] laatste wijziging op: 12-10-2008 (12-10-2008)